什么是线性规划，什么是二次规划

线性规划（运筹学术语）

线性规划（Linear programming,简称LP），是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支，它是辅助人们进行科学管理的一种数学方法。研究线性约束条件下线性目标函数的极值问题的数学理论和方法。英文缩写LP。

线性规划是运筹学的一个重要分支，广泛应用于军事作战、经济分析、经营管理和工程技术等方面。为合理地利用有限的人力、物力、财力等资源作出的最优决策，提供科学的依据。

线性规划简介

数学模型

（1）列出约束条件及目标函数

（2）画出约束条件所表示的可行域

（3）在可行域内求目标函数的最优解及最优值

 

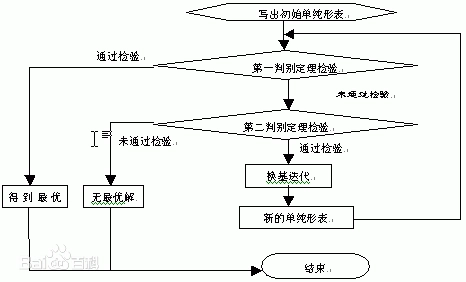
 线性规划步骤

标准型

描述线性规划问题的常用和最直观形式是标准型。标准型包括以下三个部分：

一个需要极大化的线性函数：

 　   
以下形式的问题约束：
　　

       

       

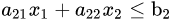
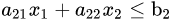
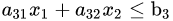
和非负变量：

       

       

其它类型的问题，例如极小化问题，不同形式的约束问题，和有负变量的问题，都可以改写成其等价问题的标准型。

来自：线性规划

二次规划

二次规划（Quadratic programming，QP问题）是非线性规划中的一类特殊数学规划问题，在很多方面都有应用，如投资组合、约束最小二乘问题的求解、序列二次规划在非线性优化问题中应用等。在过去的几十年里，二次规划已经成为运筹学、经济数学、管理科学、系统分析和组合优化科学的基本方法。

一般形式

二次规划的一般形式可以表示为：

 其中G是Hessian矩阵，τ是有限指标集，c，x和，都是R中的向量。如果Hessian矩阵是半正定的，则我们说该式是一个凸二次规划，在这种情况下该问题的困难程度类似于线性规划。如果有至少一个向量满足约束并且在可行域有下界，则凸二次规划问题就有一个全局最小值。如果是正定的，则这类二次规划为严格的凸二次规划，那么全局最小值就是唯一的。如果是一个不定矩阵，则为非凸二次规划，这类二次规划更有挑战性，因为它们有多个平稳点和局部极小值点。

 来自：二次规划