随机种子的详解

什么是随机种子？
我们知道，随机数是通过一些复杂的数学算法得到的，那么 随机种子（Random Seed）就是这些随机数的初始值。

一般计算机里面产生的随机数都是伪随机数。 伪随机数，也是就一个一直不变的数。

import numpy as np

num = 0
while (num < 5):
np.random.seed(0)
print(np.random.rand(1,5)) # 得到一个范围从0到1的 1行5列的随机数
num += 1

print('-------------------------')

结果：

由结果可以看出来，这些都是伪随机数，也就是一直不变的随机数，所以我们可以通过输入随机种子，得到一个初始固定的随机数。随机种子的初始值，是一直不变的。

我们把随机种子的赋值，放到循环外面，意思是只初始化一次

import numpy as np

num = 0
np.random.seed(0)
while (num < 5):

print(np.random.rand(1,5))
num += 1

print('-------------------------')

看到，结果就不一样了，但是初始化第一行的结果还是一样的，这说明初始值一样 ，而且你会发现，无论你运行多少遍，有了随机种子，运行的结果都是一样的

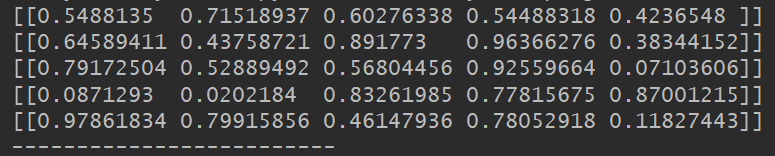
但我们不需要随机种子的时候，把随机种子的赋值注释掉

import numpy as np


num = 0
#np.random.seed(0)
while (num < 5):

print(np.random.rand(1,5))
num += 1

print('-------------------------')

 第一次结果：

 第二次结果：

 

 第三次结果：

此时结果就是完全随机，没有一点章法。

所以我总结就是，通过随机种子，通过一些复杂的数学算法，你可以得到一组有规律的随机数，而随机种子就是这个随机数的初始值。随机种子相同，得到的随机数一定也相同。

随机种子计算随机数的计算方法：

一般种子可以以当前的系统时间，这是完全随机的

算法1：平方取中法。

1）将种子设为X0，并mod 10000得到4位数

2）将它平方得到一个8位数（不足8位时前面补0）

3）取中间的4位数可得到下一个4位随机数X1

4）重复1-3步，即可产生多个随机数

这个算法的一个主要缺点是最终它会退化成0，不能继续产生随机数。

算法2：线性同余法

1）将种子设为X0，

2）用一个算法X(n+1）=(a*X(n)+b) mod c产生X(n+1）

一般将c取得很大，可产生0到c-1之间的伪随机数

该算法的一个缺点是会出现循环。

 

参考文献：
https://baijiahao.baidu.com/s?id=1625366743643510488&wfr=spider&for=pc

https://www.cnblogs.com/subic/p/8454025.html

https://blog.csdn.net/zenghaitao0128/article/details/78556535

https://baike.baidu.com/item/%E9%9A%8F%E6%9C%BA%E7%A7%8D%E5%AD%90/9844665?fr=aladdin
————————————————
版权声明：本文为CSDN博主「ding_programmer」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/ding_programmer/article/details/95097924