BGD(批量梯度下降）--学习笔记

函数凸凹性：

用到的范数知识：

详细解释：每一个元素的平方再开方。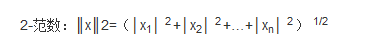

补充损失函数： Huber Loss知识点

loss函数可以通过loss参数进行设置。SGDRegressor支持以下的loss函数：

SGD:随机梯度下降四个损失函数：

事例代码：

import numpy as np 
import matplotlib.pyplot as plt
np.random.seed(0)  #随机数种子
#构造训练数据，这个数据不包括x0;
x=np.arange(0,10,0.2) #生成50个样本
#训练样本的个数
m=len(x)
#构造x0
x0=np.full(m,1.0)   #50个1
#将x0和x拼接起来，组成完整的训练数据
input_data=np.vstack([x0,x]).T  #将偏置b作为权向量的第一个分量
featureNum=input_data.shape[1]    #维度
print(input_data)
#y_train生成y，其实就是input_data对应的标签
target_data=2*x+5+np.random.randn(m)    #最后一项是偏差m=5就行了，x是50的向量

#两种终止条件
loop_max=1000000 #最大迭代次数，防止死循环
epsilon=1e-5    #阈值

#初始化权值
theta=np.random.randn(featureNum)
alpha=0.00001   #步长(注意取值过大会导致震荡即不收敛，过小收敛速度变慢)
#记录误差变量
error=np.zeros(featureNum)
count=0 #循环次数
#全部用向量表示，theta的维度和error维度一样。

while count < loop_max:
    count += 1
    sum_m=np.zeros(2)
    for i in range(m):
        diff = (np.dot(theta,input_data[i])-target_data[i])*input_data[i]
        sum_m=sum_m+diff #当alpha取值过大时，sum_m会在迭代过程中溢出

    theta = theta-alpha*sum_m   #注意步长alpha（0.005的时候会震荡）的取值，过大会导致震荡
    #判断是否已经收敛
    if np.linalg.norm(theta-error)<epsilon: #norm()范数:error是之前的theta,theta是更新后的，相减是求距离，也就是求相关性：距离很小的时候，相当于theta值没有更新
        break
    else:
        error=theta
    print('loop count=%d'%count,'\tw:',theta)
print('loop count=%d'%count,'\tw:',theta)

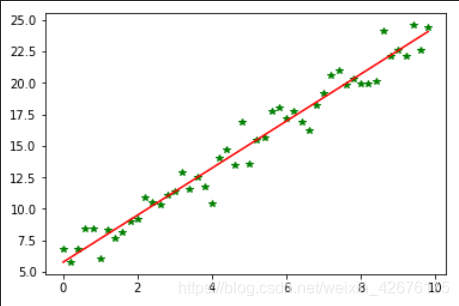
plt.plot(x,target_data,'g*')
plt.plot(x,theta[1]*x+theta[0],'r')
plt.show()

输出：
省略···