无人驾驶模型预测控制第二版（第四章仿真）

 

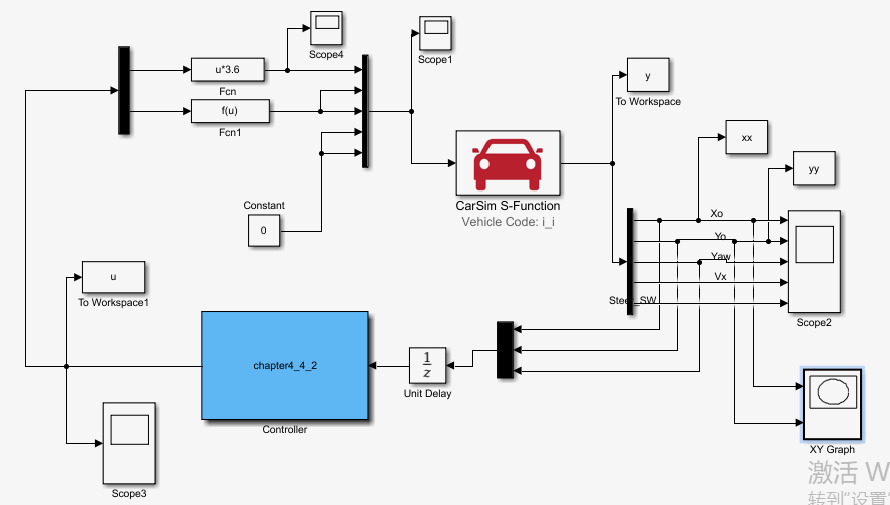
simulink中的模型（s-function中的程序放在最后，以免影响阅读）

 

 

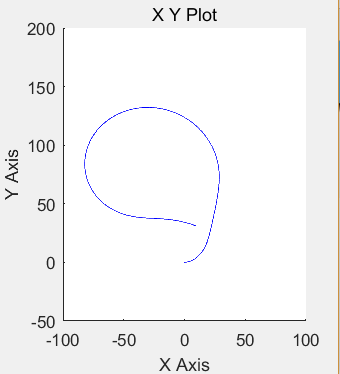
 仿真时间设置成20，仿真结果图像 { 跟踪轨迹是半径25m的圆形轨迹，圆心为（0,35））}

 

 

 仿真时间设置成30时

 

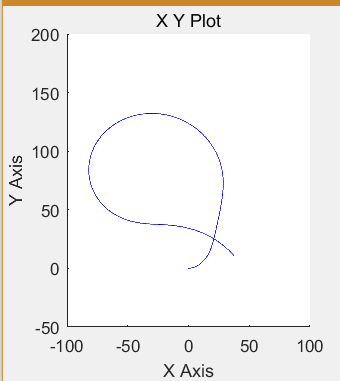
 图像中的轨迹在仿真时间20之后不再跟随轨迹，目前还没找到原因

s-function中的程序代码

function [sys,x0,str,ts] = MY_MPCController3(t,x,u,flag)
%   该函数是写的第3个S函数控制器(MATLAB版本：R2011a)
%   限定于车辆运动学模型，控制量为速度和前轮偏角，使用的QP为新版本的QP解法
%   [sys,x0,str,ts] = MY_MPCController3(t,x,u,flag)
%
% is an S-function implementing the MPC controller intended for use
% with Simulink. The argument md, which is the only user supplied
% argument, contains the data structures needed by the controller. The
% input to the S-function block is a vector signal consisting of the
% measured outputs and the reference values for the controlled
% outputs. The output of the S-function block is a vector signal
% consisting of the control variables and the estimated state vector,
% potentially including estimated disturbance states.

switch flag,
 case 0
  [sys,x0,str,ts] = mdlInitializeSizes; % Initialization
  
 case 2
  sys = mdlUpdates(t,x,u); % Update discrete states
  
 case 3
  sys = mdlOutputs(t,x,u); % Calculate outputs
 
 case {1,4,9} % Unused flags
  sys = [];
  
 otherwise
  error(['unhandled flag = ',num2str(flag)]); % Error handling
end
% End of dsfunc.

%==============================================================
% Initialization
%==============================================================

function [sys,x0,str,ts] = mdlInitializeSizes

% Call simsizes for a sizes structure, fill it in, and convert it 
% to a sizes array.

sizes = simsizes;
sizes.NumContStates  = 0;
sizes.NumDiscStates  = 3; % this parameter doesn't matter
sizes.NumOutputs     = 2; %[speed, steering]
sizes.NumInputs      = 3; % =======
sizes.DirFeedthrough = 1; % Matrix D is non-empty.
sizes.NumSampleTimes = 1;
sys = simsizes(sizes); 
x0 =[0;0;0];   
global U; % store current ctrl vector:[vel_m, delta_m]
U=[0;0];
% Initialize the discrete states.
str = [];             % Set str to an empty matrix.
ts  = [0.1 0];       % sample time: [period, offset]
%End of mdlInitializeSizes
              
%==============================================================
% Update the discrete states
%==============================================================
function sys = mdlUpdates(t,x,u)
  
sys = x;
%End of mdlUpdate.

%==============================================================
% Calculate outputs
%==============================================================
function sys = mdlOutputs(t,x,u)
    global a b u_piao;
    global U; %store chi_tilde=[vel-vel_ref; delta - delta_ref]
    global kesi;
 
    tic
    Nx=3;%状态量的个数
    Nu =2;%控制量的个数
    Np =60;%预测步长
    Nc=30;%控制步长
    Row=10;%松弛因子
    %fprintf('Update start, t=%6.3f\n',t)
    t_d =u(3)*3.1415926/180;%CarSim输出的Yaw angle为角度，角度转换为弧度

   % 直线路径
   % r(1)=5*t; %ref_x-axis
   % r(2)=5;%ref_y-axis
   % r(3)=0;%ref_heading_angle
   % vd1=5;% ref_velocity
    %vd2=0;% ref_steering

   
%     半径为25m的圆形轨迹, 圆心为(0, 35), 速度为5m/s
     r(1)=25*sin(0.2*t);
     r(2)=25+10-25*cos(0.2*t); 
     r(3)=0.2*t;
     vd1=5;                                              
     vd2=0.104;

%     %半径为35m的圆形轨迹, 圆心为(0, 35), 速度为3m/s
%     r(1)=25*sin(0.12*t);
%     r(2)=25+10-25*cos(0.12*t);
%     r(3)=0.12*t;
%     vd1=3;
%     vd2=0.104;
%     半径为25m的圆形轨迹, 圆心为(0, 35), 速度为10m/s
%      r(1)=25*sin(0.4*t);
%      r(2)=25+10-25*cos(0.4*t);
%      r(3)=0.4*t;
%      vd1=10;
%      vd2=0.104;
%     %半径为25m的圆形轨迹, 圆心为(0, 35), 速度为4m/s
%      r(1)=25*sin(0.16*t);
%      r(2)=25+10-25*cos(0.16*t);
%      r(3)=0.16*t;
%      vd1=4;
%      vd2=0.104;

    %t_d =  r(3);
    kesi=zeros(Nx+Nu,1);
    kesi(1) = u(1)-r(1);%u(1)==X(1),x_offset
    kesi(2) = u(2)-r(2);%u(2)==X(2),y_offset
    kesi(3) = t_d - r(3); %u(3)==X(3),heading_angle_offset
    %if (heading_offset < -pi)
     %   heading_offset = heading_offset + 2*pi;
   %end
   % if (heading_offset > pi)
    %    heading_offset = heading_offset - 2*pi;
    %end
   % kesi(3)=heading_offset;
    
     %U(1) = u(4)/3.6 - vd1; % vel, km/h-->m/s
     %steer_SW = u(5)*pi/180;
     %^steering_angle = steer_SW/18.0;
    % U(2) = steering_angle - vd2;
   
    kesi(4)=U(1); % vel-vel_ref
    kesi(5)=U(2); % steer_angle - steering_ref
    fprintf('vel-offset=%4.2f, steering-offset, U(2)=%4.2f\n',U(1), U(2))

    T=0.1;
    T_all=30;%临时设定，总的仿真时间，主要功能是防止计算期望轨迹越界
    % Mobile Robot Parameters
    L = 2.6; % wheelbase of carsim vehicle
    % Mobile Robot variable
    
   
    %矩阵初始化  
    u_piao=zeros(Nx, Nu);
    Q=100*eye(Nx*Np,Nx*Np);    
    R=5*eye(Nu*Nc);
    a=[1    0   -vd1*sin(t_d)*T;
       0    1   vd1*cos(t_d)*T;
       0    0   1;];
    b=[cos(t_d)*T        0;
       sin(t_d)*T        0;
       tan(vd2)*T/L      vd1*T/(cos(vd2)^2)];
  
    A_cell=cell(2,2);
    B_cell=cell(2,1);
    A_cell{1,1}=a;
    A_cell{1,2}=b;
    A_cell{2,1}=zeros(Nu,Nx);
    A_cell{2,2}=eye(Nu);
    B_cell{1,1}=b;
    B_cell{2,1}=eye(Nu);
 
    A=cell2mat(A_cell);
    B=cell2mat(B_cell);
    C=[ 1 0 0 0 0;
        0 1 0 0 0;
        0 0 1 0 0];

    PHI_cell=cell(Np,1);
    THETA_cell=cell(Np,Nc);
    for j=1:1:Np
        PHI_cell{j,1}=C*A^j;
        for k=1:1:Nc
            if k<=j
                THETA_cell{j,k}=C*A^(j-k)*B;
            else 
                THETA_cell{j,k}=zeros(Nx,Nu);
            end
        end
    end
    PHI=cell2mat(PHI_cell);%size(PHI)=[Nx*Np Nx+Nu]
    THETA=cell2mat(THETA_cell);%size(THETA)=[Nx*Np Nu*(Nc+1)]

    H_cell=cell(2,2);
    H_cell{1,1}=THETA'*Q*THETA+R;
    H_cell{1,2}=zeros(Nu*Nc,1);
    H_cell{2,1}=zeros(1,Nu*Nc);
    H_cell{2,2}=Row;
    H=cell2mat(H_cell);
    %H=(H+H')/2;

    error=PHI*kesi;
    f_cell=cell(1,2);
    f_cell{1,1} = (2*error'*Q*THETA);
    f_cell{1,2} = 0;
    f=cell2mat(f_cell);

 %% 以下为约束生成区域
 %不等式约束
    A_t=zeros(Nc,Nc);%见falcone论文 P181
    for p=1:1:Nc
        for q=1:1:Nc
            if q<=p 
                A_t(p,q)=1;
            else 
                A_t(p,q)=0;
            end
        end 
    end 
    A_I=kron(A_t,eye(Nu));%对应于falcone论文约束处理的矩阵A,求克罗内克积
    Ut=kron(ones(Nc,1), U);%
    umin=[-0.2;  -0.54];%[min_vel, min_steer]维数与控制变量的个数相同
    umax=[0.2;   0.332]; %[max_vel, max_steer],%0.436rad = 25deg
    delta_umin = [-0.05;  -0.0082]; % 0.0082rad = 0.47deg
    delta_umax = [0.05;  0.0082];

    Umin=kron(ones(Nc,1),umin);
    Umax=kron(ones(Nc,1),umax);
    A_cons_cell={A_I zeros(Nu*Nc, 1); -A_I zeros(Nu*Nc, 1)};
    b_cons_cell={Umax-Ut;-Umin+Ut};
    A_cons=cell2mat(A_cons_cell);%（求解方程）状态量不等式约束增益矩阵，转换为绝对值的取值范围
    b_cons=cell2mat(b_cons_cell);%（求解方程）状态量不等式约束的取值

   % 状态量约束
    delta_Umin = kron(ones(Nc,1),delta_umin);
    delta_Umax = kron(ones(Nc,1),delta_umax);
    lb = [delta_Umin; 0];%（求解方程）状态量下界
    ub = [delta_Umax; 10];%（求解方程）状态量上界
  
    %% 开始求解过程
%     options = optimset('Algorithm','active-set');
    options = optimset('Algorithm','interior-point-convex'); 
    warning off all  % close the warnings during computation     
    [X, fval,exitflag]=quadprog(H, f, A_cons, b_cons,[], [],lb,ub,[],options);
    fprintf('quadprog EXITFLAG = %d\n',exitflag);

    %% 计算输出   
    u_piao(1)=X(1);
    u_piao(2)=X(2);
    U(1)=kesi(4)+u_piao(1);%用于存储上一个时刻的控制量
    U(2)=kesi(5)+u_piao(2);
    u_real(1) = U(1) + vd1;
    u_real(2) = U(2) + vd2;
 
    sys= [u_real(1); u_real(2)]; % vel, steering, x, y
    toc
% End of mdlOutputs.