【Matlab】简单的滑模控制程序及Simulink仿真
文章：
这篇文章仿真和输出U的推到有些问题，博主根据此篇文章进行修改进行对sin（t）曲线的追踪（使用滑模控制）
1.前言
最近开始了对滑模控制的学习，使用的书籍为刘金琨的《滑膜变结构控制MATLAB仿真》，今天是按照书上的例程做了一个简单的自适应控制系统。
2.程序解析
此程序中，电机控制系统的动态模型为：
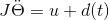，其中，θ为电机的角位置，J为转动惯量，d(t)为干扰且满足
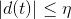，η为干扰上界，
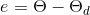为角位置跟踪误差
定义跟踪误差函数，也就是滑模面函数s为：
，当s=0时，有e和edot都为0，且是按照指数收敛：
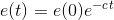
也就是说当时间趋于∞时，误差将指数收敛到0，收敛速度取决于c，所以误差函数s的收敛性意味着位置跟踪误差e和速度跟踪误差e'的收敛性，也就是说：s为滑膜函数。
2.1.控制器代码
首先是控制器的S函数。控制器就是系统的输入控制量u：
function [sys,x0,str,ts] = simple_adaptive_controller(t, x, u, flag)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes; % 调用初始化子函数
case 1,
sys=[];
case 2,
sys=[];
case 3,
sys=mdlOutputs(t,x,u); %计算输出子函数
case 4,
sys=[]; %计算下一仿真时刻子函数
case 9,
sys=[]; %终止仿真子函数
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes %初始化子函数
sizes = simsizes;
sizes.NumContStates = 0; %连续状态变量个数
sizes.NumDiscStates = 0; %离散状态变量个数
sizes.NumOutputs = 1; %输出变量个数
sizes.NumInputs = 3; %输入变量个数
sizes.DirFeedthrough = 1; %输入信号是否在输出端出现
sizes.NumSampleTimes = 0; % at least one sample time is needed
sys = simsizes(sizes);
x0 = []; %初始值
str = [];
ts = []; %[0 0]用于连续系统，[-1 0]表示继承其前的采样时间设置
simStateCompliance = 'UnknownSimState';
function sys=mdlOutputs(t,x,u) %计算输出子函数
J = 2;
thd = u(1);
th = u(2);
dth = u(3);
e = th - thd;
de = dth;
c = 10;
s = c*e + de;
xite = 1.1;
k = 0;
ut = J*(-c*dth-1/J*(k*s+xite*sign(s)));
sys(1) = ut;
因为控制器不涉及到复杂的微分运算，故只用在mdlOutputs中写控制输入u的代码
2.2.受控对象代码
本例中，受控对象为电机控制系统，，需要对这个微分方程进行描述，因为要用到θ、θ'，虽然方程中有θ''，但是可以通过除以J得到θ''的表达式，故代码如下：
function [sys,x0,str,ts] = plant(t, x, u, flag)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes; % 调用初始化子函数
case 1,
sys=mdlDerivatives(t,x,u); %调用计算微分子函数
case 2,
sys=[];
case 3,
sys=mdlOutputs(t,x,u); %计算输出子函数
case 4,
sys=[]; %计算下一仿真时刻子函数
case 9,
sys=[]; %终止仿真子函数
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes %初始化子函数
sizes = simsizes;
sizes.NumContStates = 2; %连续状态变量个数
sizes.NumDiscStates = 0; %离散状态变量个数
sizes.NumOutputs = 2; %输出变量个数
sizes.NumInputs = 1; %输入变量个数
sizes.DirFeedthrough = 0; %输入信号是否在输出端出现
sizes.NumSampleTimes = 1; % at least one sample time is needed
sys = simsizes(sizes);
x0 = [0, 0]; %初始值
str = [];
ts = [0 0]; %[0 0]用于连续系统，[-1 0]表示继承其前的采样时间设置
simStateCompliance = 'UnknownSimState';
function sys = mdlDerivatives(t, x, u) %计算微分子函数
J = 2;
dt = sin(t);
ut = u(1);
sys(1) = x(2);
sys(2) = 1/J*(ut+dt);
function sys=mdlOutputs(t,x,u) %计算输出子函数
sys(1) = x(1);
sys(2) = x(2);
3.仿真结果和Simulink注意事项
Simulink建立如下模型：
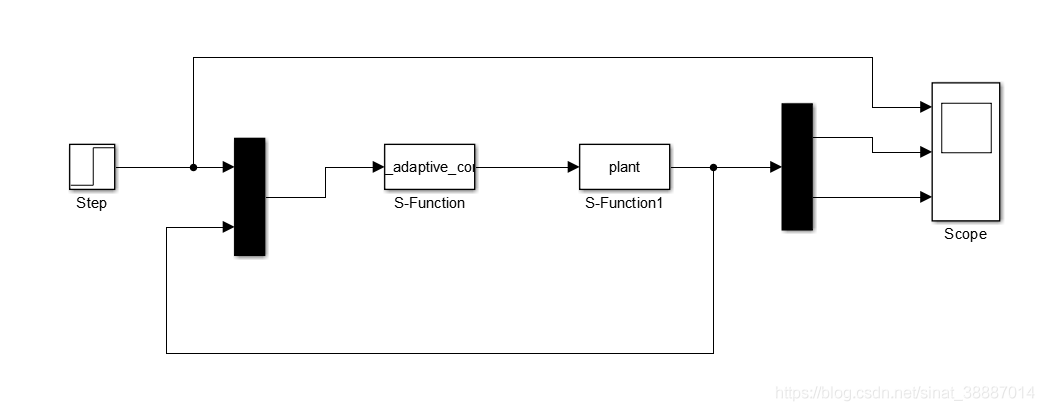
将微分方程算法换为定步长fixed step中的ode4！不然仿真超级慢！
具体分析可见：https://www.ilovematlab.cn/thread-260054-1-1.html
最后结果为：
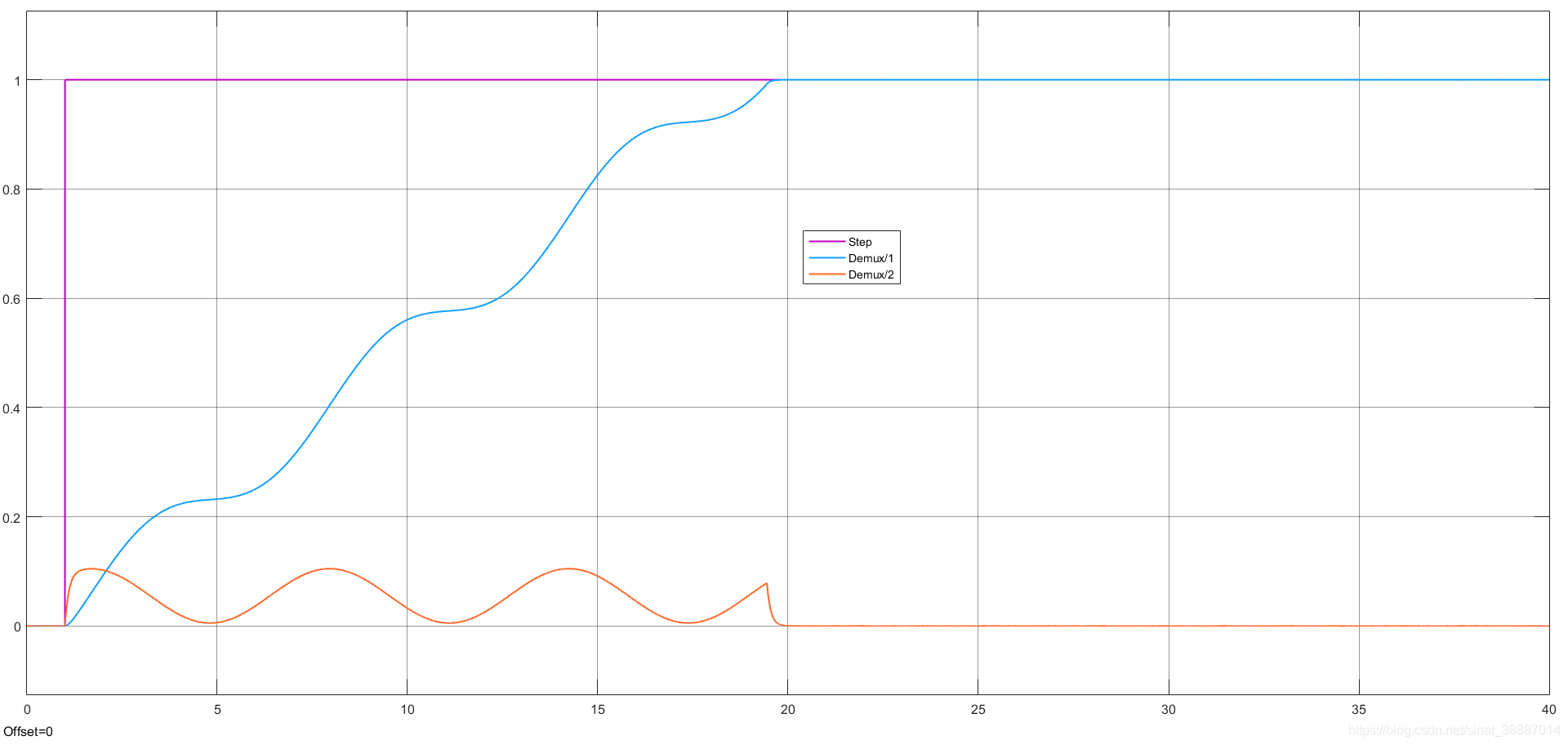
系统最终能够跟踪阶跃信号
————————————————
版权声明：本文为CSDN博主「PriscillaSCU」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/sinat_38887014/article/details/103115218
