线性系统非线性系统的自我理解

线性系统

什么是线性系统

线形指量与量之间按比例、成直线的关系，在空间和时间上代表规则和光滑的运动；

如何判断一个系统是线性系统还是非线性系统（实际中的问题都是非线性）

以状态方程来说明

线性时变系统系数矩阵不随时间变化

线性是不变系统系数矩阵不随时间变化即为常数矩阵

线性时变系统       式1.1

线性非时变系统 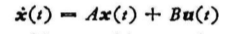       式1.2

可以化成上面两种情况的，就是线性系统

举一个有意思的例子

y=kx+b是不是线性的

如果将x看成变量，按照叠加原理，

<1>x1、x2是方程的解，即y1 = k*x1 +b；y2 = k*x2 +b

<2>假设x3=x1 + x2；

<3>带入方程 y3 = k*(x1 + x2) +b = k*x1 + k*x2 +b;

<4>验证如果满足叠加原理则y1 + y2 = y3；  明显并不满足y1 + y2 比 y3多一个常量b

故此方程不算是线性；

但是你如果定义x'=[x;b],定义k’= [k, 1],那么方程就变成y=k’*  x'; 根据上面几步很容易判断此方程是线性的。

其实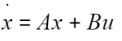将x作为单独变量也不满足叠加原理，和y=kx+b的情况差不多，如果将方程写作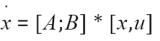定义X’=[x,u]，K’=[A;B],再看这个方程这不就满足叠加原理了吗。

所以再看一个系统是不是线性系统时，首先看哪些作为状态变量X，哪些作为控制量U，之后看是不是能化成式1.1和式1.2的形式，可以化成就是线性系统。

在无人驾驶模型预测控制书中

 

问公式4.1是不是线性系统；直接什么条件也没给这个是不能判断的；

说明两种情况

（1）将，那个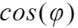列矩阵看成时变的系数矩阵B(t)，所以方程就变成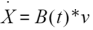，你看这是不是满足叠加原理呢

（2）如果以书上的输入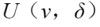量，状态变量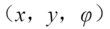，是化不成公式1.1或者1.2在这种形式的，应为deta在tan里面。

所以在判断一个系统是不是线性时，应该首先明确我们要研究这个系统的那些量，那些作为状态量X，那些作为控制量U，应为选取量的不同最终判断结果也不同

线性系统的特征

线性系统满足叠加原理

 

线性系统的优点

稳定性容易判断

1、已传递函数形式来说，可以通过极点分布情况判断系统稳定性，极点分布在s平面的左侧系统稳定

2、以状态方程的形式来说，状态变的系数矩阵的特征值全小于0，系统稳定

线性系统的模型容易算的控制量

比如通过状态反馈来找到合适的控制量U（可以通过系数矩阵特征值来判断U是否能让系统稳定）

非线性系统

非线性系统不是很好研究，判断稳定性时可以用李雅普诺夫方法进行判断，但是不如线性系统容易，线性系统研究更加容易，所以需要用一种方法将非线性进行线性化；这就要说到高数中的泰勒公式

 

 

 线性化的限制