一个模型预测控制(MPC)的简单实现
1 生活中的启示
情景如下:你们团队每天早晨开一次例会,主要会议内容是你汇报工作进度,领导根据工作目标和工作进度,制定当天的工作计划,你领到工作计划后开始工作。每天都这样周而复始,从领导的角度看,这件工作实现了“闭环”,工作进度“可控”,这就是闭环控制系统。

图1 闭环控制系统
不同的领导(控制器)水平有高又低,按照介绍控制器先踩一脚PID的国际惯例,设:

则PID控制器的控制律为:
从该控制律中我们可以看到PID的两个问题:
1, PID控制器不具有“前瞻性”:参与计算的各个量,有当前的 ,上个控制周期的
,以及之前所有的
累计和,偏偏没有未来的
。这个“领导”目光过于短浅,只求今天能完成任务,哪怕第二天公司就倒闭了,那也是第二天要解决的麻烦,今天该干啥干啥。
2, PID属于无模型控制。作为一个“领导”,PID仅仅通过工作目标和工作进度上的差距,以及三个近乎魔法般的数字,就制定了工作计划,完全不考虑你的工作能力和这项工作的难度,这是非常失职的。
为了提高工作的的可行性,经过思考,我们还可以有另一种方案:
- 领导听完你的汇报后,根据工作进度(系统状态)、工作目标(参考值)、你的工作能力和任务难度(系统模型),制定了未来10天的工作计划,每一天要干什么都写得清清楚楚明明白白。
- 领导将这十天计划里面第一天的计划交给你,剩下九天的计划销毁。
- 第二天重复上述过程。
显然第二种方案更具有可行性,它能根据任务的完成情况及时调整工作计划,同时兼顾了未来的工作计划、你的工作能力和任务的难度,更符合我们的认知。
当然这种方案还有一点小缺陷,比如“剩下九天计划销毁”,领导看了这个方案肯定心里不舒服,辛辛苦苦做的计划凭什么销毁呢?为了弥补这个缺陷,我们提出了“控制时域”和“预测时域”的概念。控制时域是指领导做多少天的计划,预测时域是指领导思考多长远的进度。比如,领导考虑到计划跟不上变化,想太长远没意义,就先做了五天的计划(控制时域是五天),然后第6-10天的计划和第5天的计划一模一样,领导预测了下按照这样的十天计划,十天后进度完成的还算可以(预测时域是十天)。这样依然给你第一天的计划,销毁剩下九天的计划,领导的工作量却少了许多。
模型预测控制的基本思想就蕴含在上述过程中,它利用一个已有的模型、系统当前的状态和未来的控制量,来预测系统未来的输出,然后与我们期望的系统输出做比较,得到一个损失函数,即:
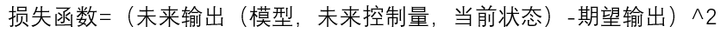
由于上式中模型、当前状态、期望输出都是已知的,因此只有未来控制量一个自变量。采用二次规划的方法求解出某个未来控制量,使得损失函数最小,这个未来控制量的第一个元素就是当前控制周期的控制量。
2 实际控制的例子
2.1 问题描述
在无限光滑的一维水平直线上有一个质量为 的滑块,初始位置与初始速度都为0,现需要设计控制器,在传感器测得滑块位置
的基础上,为滑块提供外力
,使其跟随参考点
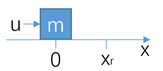
图2 例图
2.2 预测模型
首先建立动力学方程:
选取状态向量 (除非特殊说明,后文中x表示状态向量,而不是滑块位置),构建系统状态方程为:
其中 。
2.3 预测模型离散化
采用前向欧拉法将状态方程离散化:
其中 ,T为控制周期。
2.4 预测
MPC方法的一个独特之处就是需要对未来系统状态进行预测,我们记未来 个控制周期内预测的系统状态为:
称为预测时域,括号中
表示在当前
时刻预测
时刻的系统状态,以此类推。另外,预测动态系统未来状态时,还需要知道预测时域内的控制量
:
这是我们接下来将要求解的优化问题的独立变量。
现在,我们可以通过离散化状态方程依次对未来 个控制周期的系统状态进行预测:
整合成矩阵形式:
其中,psi : , theta :
上式中的下三角形式,直接反映了系统在时间上的因果关系,即 时刻的输入对
时刻的输出没有影响,
时刻的输入对
和
时刻没有影响,等等。
2.5 优化
这一节我们将求解预测时域内的控制输出 ,在求解优化问题之前,我们首先明确优化问题的数学描述。
我们的控制目标是使系统的状态跟踪期望的一条轨迹,通常称为参考值,定义预测时域内的参考值序列:
注意,在 时刻进行控制的时候,控制器就必须已经得到了
时刻到
时刻的参考值,而PID就不需要这么多信息,这是MPC的一个缺点。
我们希望寻找最佳的控制量 ,使得预测时域内的状态向量与参考值越接近越好,这是一个开环最优控制问题。为此,我们用预测状态向量与参考值之间的累计误差定义一个简单的优化目标函数:
经常地,我们不希望控制动作太大,优化目标函数再添加一项对控制量的约束:
因此,该优化问题可以描述如下:
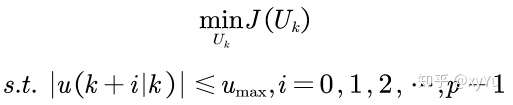
我们将优化函数 展开后合并同类项:
注意::::::::
在这里如果你仔细去化简上面的公式,会发现一个问题 2 ET* Q * thita * U是怎么来的,化简的结果应该是ET* Q * thita * U和UT*thitaT*Q*E,为什么上面的结果是 2 ET* Q * thita * U,难道说ET* Q * thita * U和UT*thitaT*Q*E相等不成,是的,这两个式子确实相等,但这两个是各自的转置后的形式啊(Q是对角矩阵,转置和原来一样这个应该没啥疑问),怎么相等呢,这和我们认知的矩阵转置一般不等于原矩阵不符啊,等等因为这个特殊呗,特殊形式中对角矩阵算一个,那这个是什么特殊情况呢?别急,我推导一遍你就清楚了。

上式中 是常数项,对“
为何值时
取得最小值”这一问题没有影响,因此直接舍去。
如图3,matlab输入 “help quadprog”查看二次型优化函数quadprog的说明文档,令:
可得最终优化目标函数,至此可直接调用matlab quadprog函数求解 ,将
的第一个元素提取出来,作为本控制周期的控制量。


图3 matlab quadprog函数
2.6 仿真
对于2.1中例子的动力学方程:
两边同时拉普拉斯变换:
可得传递函数:
在simulink中搭建仿真环境如图4,并编写MPC控制器(2.2—2.5):
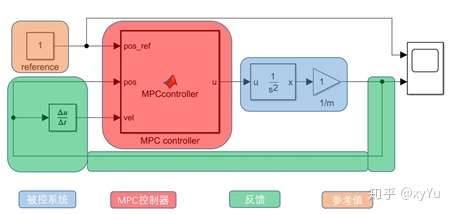

图4 simulink中仿真
1 function u = MPCcontroller(pos_ref, pos, vel)
2 %参数设置
3 m = 1.05; %滑块质量,增加了5%作为建模误差
4 T = 0.01; %控制周期10ms //采样时间
5 p = 45; %控制时域(预测时域)
6 Q = 10*eye(2*p); %状态误差权重 //因为Xk中有两个状态变量所以P乘以2以下道理相同
7 W = 0.0001*eye(p); %控制输出权重
8 umax = 100; %控制量限制,即最大的力
9 Rk = zeros(2*p,1); %参考值序列
10 Rk(1:2:end) = pos_ref;%参考位置由函数参数指定
11 Rk(2:2:end) = vel; %参考速度跟随实际速度
12 %构建中间变量
13 xk = [pos;vel]; %xk
14 A_ = [1 T;0 1]; %离散化预测模型参数A
15 B_ = [0;T/m]; %离散化预测模型参数B
16 psi = zeros(2*p,2); %psi
%构建psi
17 for i=1:1:p
18 psi(i*2-1:i*2,1:2)=A_^i;
19 end
%构建theta
20 theta = zeros(2*p,p); %theta
21 for i=1:1:p
22 for j=1:1:i
23 theta(i*2-1:i*2,j)=A_^(i-j)*B_;
24 end
25 end
26 E = psi*xk-Rk; %E
27 H = 2*(theta'*Q*theta+W); %H
28 f = (2*E'*Q*theta)'; %f
29 %优化求解
30 coder.extrinsic('quadprog');
31 Uk=quadprog(H,f,[],[],[],[],-umax,umax);
32 %返回控制量序列第一个值
33 u = 0.0; %指定u的类型
34 u = Uk(1); %提取控制序列第一项
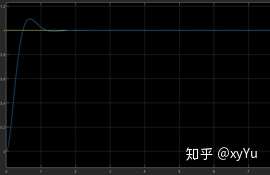
p=40,仿真结果
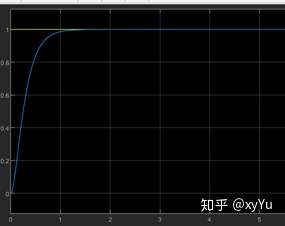
p=60,仿真结果
参考文献
陈虹. 模型预测控制[M]. 科学出版社, 2013.
龚建伟, 姜岩, 徐威. 无人驾驶车辆模型预测控制[M]. 北京理工大学出版社, 2014.
转自:https://zhuanlan.zhihu.com/p/141871796?utm_source=wechat_session

