LQR (线性二次型调节器)的直观推导及简单应用
转自:https://blog.csdn.net/heyijia0327/article/details/39270597
本文主要介绍LQR的直观推导,说明LQR目标函数J选择的直观含义以及简单介绍矩阵Q,R的选取,最后总结LQR控制器的设计步奏,并将其应用在一个简单的倒立摆例子上。
假设有一个线性系统能用状态向量的形式表示成:
![]()
![]() ( 1 )
( 1 )
其中 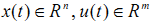
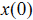
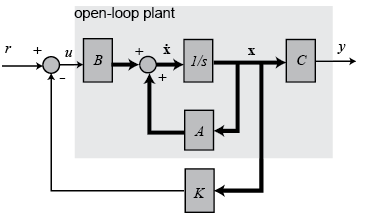
在介绍LQR前,先简单回顾一下现代控制理论中最基本的控制器--全状态反馈控制。
全状态反馈控制系统图形如下:
我们要设计一个状态反馈控制器
使得闭环系统能够满足我们期望的性能。我们把这种控制代入之前的系统状态方程得到
![]() ( 2 )
( 2 )
对于(1)式的开环系统,由现代控制理论我们知道开环传递函数的极点就是系统矩阵A的特征值。
(传递函数的分母是|s| -A|,|·|表示行列式)
现在变成了(2)的闭环形式,状态变换矩阵A变成了(A-BK)。因此通过配置反馈矩阵K,可以使得闭环系统的极点达到我们期望的状态。注意,这种控制器的设计与输出矩阵C,D没有关系。
那么,什么样的极点会使得系统性能很棒呢?并且,当系统变量很多的时候,即使设计好了极点,矩阵K也不好计算。
于是,LQR为我们设计最优控制器提供了一种思路。
在设计LQR控制器前,我们得设计一个能量函数,最优的控制轨迹应该使得该能量函数最小。一般选取如下形式的能量函数。
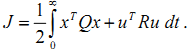
其中Q是你自己设计的半正定矩阵,R为正定矩阵。
可是,为什么能量函数(或称系统的目标函数)得设计成这个样子呢?
首先假设状态向量x(t)是1维的,那么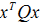
同理. 能量函数J要最小,那么状态向量x(t),u(t)都得小。J最小,那肯定是个有界的函数,我们能推断当t趋于无穷时,状态向量x(t)将趋于0,这也保证了闭环系统的稳定性。那输入u(t)要小是什么意思呢?它意味着我们用最小的控制代价得到最优的控制。譬如控制电机,输入PWM小,将节省能量。
再来看看矩阵Q,R的选取,一般来说,Q值选得大意味着,要使得J小,那x(t)需要更小,也就是意味着闭环系统的矩阵(A-BK)的特征值处于S平面左边更远的地方,这样状态x(t)就以更快的速度衰减到0。另一方面,大的R表示更加关注输入变量u(t),u(t)的减小,意味着状态衰减将变慢。同时,Q为半正定矩阵意味着他的特征值非负,R为正定矩阵意味着它的特征值为正数。如果你选择Q,R都是对角矩阵的话,那么Q的对角元素为正数,允许出现几个0.R的对角元素只能是正数。
注意LQR调节器是将状态调节到0,这与轨迹跟踪不同,轨迹跟踪是使得系统误差为0。
轨迹跟踪实现方案线性二次型控制器(LQR)——轨迹跟踪器
知道了背景后,那如何设计反馈矩阵K使得能量函数J最小呢?
很多地方都是从最大值原理,Hamilton函数推导出来。这里用另外一种更容易接受的方式推导。
将u = -Kx 代入之前的能量函数得到:
 ( 3 )
( 3 )
为了找到K,我们先不防假设存在一个常量矩阵P使得:
![]() (4)
(4)
代入(3)式得:
 (5)
(5)
注意,我们已经假设闭环系统是稳定的,也就是t趋于无穷时,x(t)趋于0.
现在把(4)式左边的微分展开,并把状态变量x的微分用(2)式替代得到:
这个式子要始终成立的话,括号里的项必须恒等于0.

这是一个关于K的二次型等式,当然这个二次型是我们不愿看到的,因为计算复杂。现在只要这个等式成立,我们何必不选择K使得两个二次项正好约掉了呢?这样既符合了要求,又简化了计算。
取 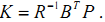 代入上式得:
代入上式得:
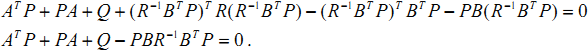
K的二次项没有了,可K的取值和P有关,而P是我们假设的一个量,P只要使得的(6)式成立就行了。而(6)式在现代控制理论中极其重要,它就是有名的Riccati 方程。
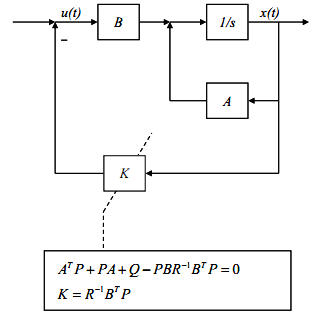
现在回过头总结下LQR控制器是怎么计算反馈矩阵K的:
1.选择参数矩阵Q,R
2.求解Riccati 方程得到矩阵P
3.计算
再看看LQR的结构图:
关于它的应用呢,比较典型的就是倒立摆控制器的设计。
倒立摆的状态变量为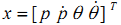
A = [0 1 0 0
0 0 -1 0
0 0 0 1
0 0 9 0];
B = [0;0.1;0;-0.1];
C = [0 0 1 0]; %观测角度
D = 0;
Q = [1 0 0 0
0 1 0 0
0 0 10 0
0 0 0 10
];
R = 0.1;
%由上面这个系统,可以计算出K
K = lqr(A,B,Q,R);
Ac = A - B*K;
%对系统进行模拟
x0 = [0.1;0;0.1;0]; %初始状态
t = 0:0.05:20;
u = zeros(size(t));
[y,x]=lsim(Ac,B,C,D,u,t,x0);
plot(t,y);
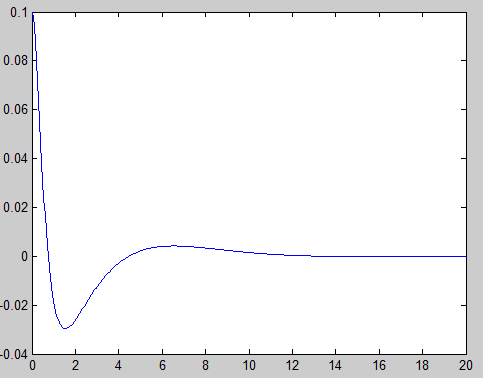
最后看到角度回到0,即平衡位置,控制器起到了作用,你可以选择不同的Q,R进行对比。
文章为总结性文章,有纰漏,请指出,谢谢。
reference:
1.F.L. Lewis .<< Linear Quadratic Regulator (LQR) State Feedback Design >>
2.http://ctms.engin.umich.edu/CTMS/index.php?example=InvertedPendulum§ion=ControlStateSpace
3.http://ctms.engin.umich.edu/CTMS/index.php?example=InvertedPendulum§ion=ControlStateSpace

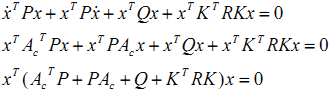
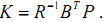



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· winform 绘制太阳,地球,月球 运作规律
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)