ZOJ 2753 Min Cut (Destroy Trade Net)(无向图全局最小割)
题目大意
给一个无向图,包含 N 个点和 M 条边,问最少删掉多少条边使得图分为不连通的两个部分,图中有重边
数据范围:2<=N<=500, 0<=M<=N*(N-1)/2
做法分析
典型的无向图全局最小割,使用 Stoer-Wagner 算法
Stoer-Wagner 算法共执行 n-1 次 BFS,每次 BFS 得到一个当前图的最小 S-T 割,并且将最后 BFS 的两个点缩点,n-1 次 BFS 得到 n-1 个最小 S-T 割中的最小者就是整个无向图的全局最小割,为了讲述每次 BFS 执行的操作,先进行如下定义:
令 g[i][j] 表示边 (i, j) 的权值,对于无向图,我们有 g[i][j]=g[j][i]
令 w[u] 表示 u 和已经被 BFS 过的点的关联度,即 w[u]=∑g[v][u] 其中,v 是已经被 BFS 过的点,u 是未被 BFS 的点。初始时,所有点的 w 值全部为 0
令 vs[u] 表示 u 是否已经被 BFS 过,vs[u]=1 表示 u 已经被 BFS 过。初始时,所有点的 vs 值全部为 0
每次 BFS 按如下步骤执行:
1. 选出未被 BFS 过的点中,关联度(w 值)最大的点(如果有多个,任选一个),设为 u。如果所有的点都已经被 BFS 过,则退出当前 BFS 过程
2. 用 u 更新所有未被 BFS 的点的关联度,即: w[v]+=g[u][v],其中 v 没有被 BFS 过
3. 将 u 设置为 BFS 过,即将 vs[u] 的值由 0 变为 1
设倒数第 2 个被 BFS 的点为 S,倒数第 1 个被 BFS 的点为 T,那么,w[T] 就是本次 BFS 得到的最小 S-T 割
每次 BFS 后,将最后 BFS 的两个点 S 和 T 缩成一个点 u,即:g[i][u]=g[i][S]+g[i][T]
每次 BFS 后,用得到的最小 S-T 割更新全局的最小割
n-1 次 BFS 后,全局最小割求出来了,图也被缩成了一个点
下面是一个例子
假设在进行 BFS 时有一个无向图如下:
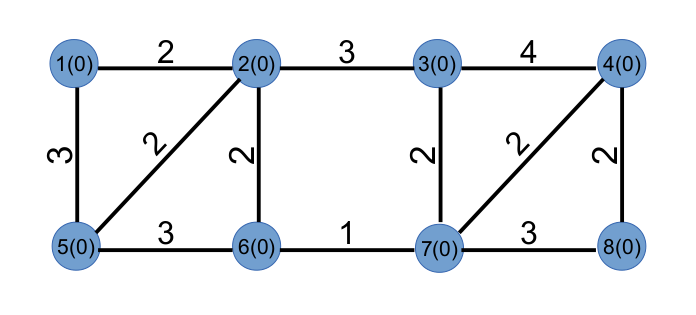
图中,括号中的数字表示每个点的 w 值,初始化为 0,边上的值表示边权。现在选择一个具有最大关联度(w 值最大)的点,有多种选择时随意选取一个点,假设选取的是第 2 个点,将它标记为已经访问过的点,并更新其他未被访问过的点的关联度:

现在,第 3 个点的关联度最大,选它作为下一个 BFS 的点,将它标记为已经访问过的点,并用它更新其他未被访问过的点的关联度:

第 4 个点的关联度最大,选其作为下一个 BFS 的点,将它标记为已经访问过的点,并更新其他未被访问过的点的关联度:

第 7 个点的关联度最大,选其作为下一个 BFS 的点,将它标记为已经访问过的点,并更新其他未被访问过的点的关联度:

第 8 个点的关联度最大,选其作为下一个 BFS 的点,将它标记为已经访问过的点,并更新其他未被访问过的点的关联度:

第 6 个点的关联度最大,选其作为下一个 BFS 的点,将它标记为已经访问过的点,并更新其他未被访问过的点的关联度:

第 5 个点的关联度最大,选其作为下一个 BFS 的点,将它标记为已经访问过的点,并更新其他未被访问过的点的关联度:

第 1 个点的关联度最大,选其作为下一个 BFS 的点,将它标记为已经访问过的点,并更新其他未被访问过的点的关联度:

至此,所有的点都被 BFS 了一遍,最后访问的点是 1,倒数第二访问的点是 5:

那么,我们这次 BFS 的 S 点是 5,T 点是 1,这次 BFS 得到的最小 S-T 割为 w[T]=5(上图中绿色的点)
将 S 点和 T 点合并:

得到新图:

将所有的标记(包括关联度,是否访问过)清空,进行下一次 BFS ,直至所有的点缩成一个点为止:

这样,经过 n-1 次 BFS 之后,整个无向图的全局最小割就求出来了
时间复杂度不难分析:o(n^3)
但是,我想,如果在每次 BFS 的时候,就像 Dijkstra 一样用堆优化,应该可以把复杂度降低到 o(n^2log2(n))
详细证明,请看 A Simple Min-Cut Algorithm
参考代码

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 5 using namespace std; 6 7 struct Stoer_Wagner { 8 static const int N=506, INF=(1<<30); 9 int G[N][N], W[N], Merge[N], S, T, minCut, n; 10 bool vs[N]; 11 12 void init(int _n) { 13 n=_n; 14 memset(G, 0, sizeof G); 15 } 16 17 void BFS() { 18 memset(vs, 0, sizeof vs); 19 memset(W, 0, sizeof W); 20 S=T=-1; 21 int Max, id; 22 for(int cnt=0; cnt<n; cnt++) { 23 Max=-INF; 24 for(int i=0; i<n; i++) 25 if(!Merge[i] && !vs[i] && W[i]>Max) 26 Max=W[i], id=i; 27 if(id==T) return; 28 S=T, T=id; 29 minCut=Max; 30 vs[id]=1; 31 for(int i=0; i<n; i++) { 32 if(Merge[i] || vs[i]) continue; 33 W[i]+=G[id][i]; 34 } 35 } 36 } 37 38 int StoerWagner() { 39 memset(Merge, 0, sizeof Merge); 40 int ans=INF; 41 for(int cnt=1; cnt<n; cnt++) { 42 BFS(); 43 if(minCut<ans) ans=minCut; 44 if(ans==0) return ans; 45 Merge[T]=1; 46 for(int i=0; i<n; i++) { 47 if(Merge[i]) continue; 48 G[S][i]+=G[T][i]; 49 G[i][S]+=G[i][T]; 50 } 51 } 52 return ans; 53 } 54 }; 55 56 Stoer_Wagner fuck; 57 int n, m; 58 59 int main() { 60 while(scanf("%d%d", &n, &m)!=EOF) { 61 fuck.init(n); 62 for(int i=0, a, b, c; i<m; i++) { 63 scanf("%d%d%d", &a, &b, &c); 64 fuck.G[a][b]+=c; 65 fuck.G[b][a]+=c; 66 } 67 printf("%d\n", fuck.StoerWagner()); 68 } 69 return 0; 70 }
题目链接 & AC 通道
ZOJ 2753 Min Cut (Destroy Trade Net)




