URAL 1549 Another Japanese Puzzle（构造）

 

题目大意

 

构造一条闭合路线，使得路线不能相交，并且走直线的步数小于等于 S，转弯（左转和右转）的步数小于等于 T。（0≤S,T≤1000）

求一条最长的路线

 

做法分析

 

注意到，因为要求路线闭合，那么转弯的数量 T 必须大于等于 4，否则无解。

适当 YY 下：只能用偶数个 S 和偶数个 T，不然不可能构成闭合路径。怎么证明，不会...

 

情况1：S<2

 

        这种情况下，我们不能使用直走的命令，只能通过不断的转弯来实现题目要求的路径，在纸上画了画，大致图形如下：

        T=4 时：   T=8：没有   T=12：    T=16： ？

       仔细观察 T=4 时候的图形和 T=12 时的图形，看能不能把 T=4 的时候的图形添加进 T=12 时的图形中，构成 T=16 时的图形？

       仔细想想之后...

       下面是我的构造方法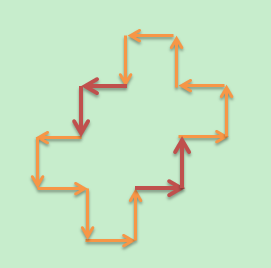：，当然，还有其他的方法，不过都大同小异

       知道了怎么由 T=12 构造 T=16 的情况，不难得到由 T=16 构造 T=20 的方法，以及之后的构造方法

       

       不难得到 T≥12 时，构造的通项公式：RLLRLL(RL)xRLLRLL(RL)x   其中， x=(T-12)/4

       当 T<12 时，只有一种情况：LLLL

       至此，情况1已经解决

 

情况2：S≥2

 

       这种情况下，我们需要使用 S 来走直线，具体是怎么做呢？

       首先需要 4 个 LLLL 使路径有成为闭合路径的可能。还剩下 [(T-4)/2]*2 的弯要转，为了让转弯之后扔然保持原来的运动方向，我把 LR 捆在一起，即左转和右转配合。首先令：x=(T-4)/2，表示有几对 LR，然后再分类讨论：

       1、x 是偶数

       不难想到，我可以先直着走，再走 LR，再转弯，到达另一边，再直着走，再转弯到达第三边，然后直着走，接着走 LR，再转弯，到达第四边，直着走，再转弯，回到出发点。如果路径严格对称的话，中间肯定不相交。怎么保证能够回到出发点呢构成闭合路径呢？看看下面的图：

       当 x=2（T=8 或 9），S=2 或 3 时的路径图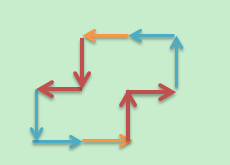：，其中：蓝色表示转弯到达另一边，橙色表示直走，深红色表示 LR 对

       根据这个，不难得出当 x 等于偶数时候的通项公式：FS/2(LR)(T-4)/4LLFS/2(LR)(T-4)/4LL

       2、x 是奇数

       和 x 是偶数时的走法差不多，虽然不能使路径严格对称，不过还是可以办到的，为了便于说明，先给一张图

       当 x=3（T=10 或 11），S=4 或 5 时的路径图： 不同颜色代表的意义还是和上面一幅图相同

       稍稍分析上面的图，不难得出当 x 等于奇数时候的通项公式：F(S-2)/2(LR)[(T-4)/4]+1LLFS/2(LR)(T-4)/4LFL

 

至此，所有情况考虑完全了...

做出来这题，好大的满足感啊！

 

参考代码

 

 1 #include <iostream>
 2 #include <cstring>
 3 #include <cstdio>
 4 
 5 using namespace std;
 6 
 7 int F, T;
 8 
 9 int main()
10 {
11     while(scanf("%d%d", &F, &T)!=EOF)
12     {
13         if(T<4)
14         {
15             printf("Atawazu\n");
16             continue;
17         }
18         if(F<2)
19         {
20             if(T<12)
21             {
22                 printf("4\nLLLL\n");
23                 continue;
24             }
25             else
26             {
27                 printf("%d\n", 12+((T-12)/4)*4);
28                 int x=(T-12)/4;
29                 printf("RLLRLLRL");
30                 for(int i=0; i<x; i++) printf("RL");
31                 printf("LRLL");
32                 for(int i=0; i<x; i++) printf("RL");
33                 printf("\n");
34                 continue;
35             }
36         }
37         printf("%d\n", (F/2)*2+(T/2)*2);
38         int x=(T-4)/2;
39         if(x%2==0)
40         {
41             for(int i=0; i<F/2; i++) printf("F");
42             for(int i=0; i<x/2; i++) printf("LR");
43             printf("LL");
44             for(int i=0; i<F/2; i++) printf("F");
45             for(int i=0; i<x/2; i++) printf("LR");
46             printf("LL");
47         }
48         else
49         {
50             for(int i=0; i<F/2-1; i++) printf("F");
51             for(int i=0; i<=x/2; i++) printf("LR");
52             printf("LL");
53             for(int i=0; i<F/2; i++) printf("F");
54             for(int i=0; i<x/2; i++) printf("LR");
55             printf("LFL");
56         }
57         printf("\n");
58     }
59     return 0;
60 }
URAL 1549

 

题目连接 & AC通道

 

URAL 1549 Another Japanese Puzzle

 

 

 

posted @ 2013-07-15 21:13  jianzhang.zj  阅读(428)  评论(0)  编辑  收藏  举报