Distinct Subsequences

　　对于有两个字符串的问题，比较常见的方法就是递归或者动态规划，而通常递归会超时。这题一看就知道递归肯定会超时，DP就成为解题利器了。前面总结过，DP一个很重要的问题是要解决意义问题：即dp[i][j]到底表示什么。对这题而言，容易想到dp[i][j]就表示模板串T的前i个字符在母串S的前j个字符中出现的次数。通常，解决了意义问题，接下来的问题就简单了，即写出递归方程。但是这题仍然让我费了好大劲，因为这题的递归方程首先不好找，其次找到了也难以理解。

　　一. 找递归方程

　　如果思路不是很清楚，那先把图画一画。

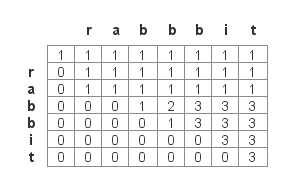
　　仔细找能够发现:

　　方程a. 如果T[i-1]!=S[j-1]，则DP[i][j]=DP[i][j-1]。

　　方程b. 如果T[i-1]==S[j-1]，则DP[i][j]=DP[i][j-1]+DP[i-1][j-1]。

 

　　二. 理解思路

　　关于上述递归方程，方程a比较容易理解，而方程b就比较难。对于方程b的理解，以下面为例子：

　　假设现在现在匹配Ta->Sa，模式串的末尾和母串的末尾相等，都是字符a。则它的值应该是T->S加上Ta->S。为什么是这样？T->S表示两个末尾的a严格对应，Ta->S则表示模式串的a对应的是S中已经包含的a。这样两部分加起来就是所有的出现的子串。

　　基于上述说明，不难写出代码:

public class Solution {
    public int numDistinct(String S, String T) {
        int[][]dp=new int[T.length()+1][S.length()+1];
        int i,j;
        for(j=0;j<=S.length();j++)
        {
            dp[0][j]=1;
        }
        for(i=1;i<=T.length();i++)
        {
            dp[i][0]=0;
        }
        for(i=1;i<=T.length();i++)
        {
            for(j=1;j<=S.length();j++)
            {
                dp[i][j]=dp[i][j-1];
                if(T.charAt(i-1)==S.charAt(j-1)){
                    dp[i][j]+=dp[i-1][j-1];
                }
            }
        }
        return dp[T.length()][S.length()];
    }
}