Master Theorem

关于时间复杂度分析,算法导论中介绍了master theorem。不过我发现和网上看到的一些版本不一样。主要区别就在于情形二。后来经过对比，发现网上的一些版本是覆盖了算法导论中介绍的情况的。维基百科上的说得比较清楚，鉴于master theorem的重要性，记于此。

递推关系式：

$T(n) = a \; T\!\left(\frac{n}{b}\right) + f(n)$ ，其中 $a \geq 1 \mbox{, } b > 1$

如果存在常数 $\epsilon > 0$ ，有

　　 $f(n) = O\left( n^{\log_b (a) - \epsilon} \right)$ ，那么

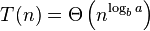
　　 $T(n) = \Theta\left( n^{\log_b a} \right)$

如果存在常数k ≥ 0，有

　　 $f(n) = \Theta\left( n^{\log_b a} \log^{k} n \right)$ ，那么

　　 $T(n) = \Theta\left( n^{\log_b a} \log^{k+1} n \right)$

如果存在常数 $\epsilon > 0$ ，有

$f(n) = \Omega\left( n^{\log_b (a) + \epsilon} \right)$ ，

同时存在常数 $c < 1$ 以及充分大的 $n$ ，满足

$a f\left( \frac{n}{b} \right) \le c f(n)$

那么

$T\left(n \right) = \Theta \left(f \left(n \right) \right)$

posted on 2013-05-26 09:40 zhizhizhiyuan 阅读(292) 评论(0) 编辑收藏举报

刷新页面返回顶部

zhizhizhiyuan