模型选择的一些基本思想和方法

原文：http://cos.name/2015/08/some-basic-ideas-and-methods-of-model-selection/

作者：高涛  编辑：王小宁

0. 引言

有监督学习是日常使用最多的建模范式，它有许多更具体的名字，比如预测模型、回归模型、分类模型或者分类器。这些名字或来源统计，或来源于机器学习。关于统计学习与机器学习的区别已经有不少讨论，不少人认为机器学习侧重于目标预测，而统计学习侧重于机制理解和建模。个人更加直观的理解是，统计学习侧重于从概率分布来描述数据生成机制，除了预测之外，还关心结果（参数假设、误差分布假设）的检验，而机器学习侧重于从函数拟合角度来描述数据生成机制，基本目的就是为了拟合和预测，缺乏严谨的参数、误差的检验机制，比如下式：

Y=f(X)+ϵY=f(X)+ϵ

 

1. 统计学习目标是获取Pr(Y|X)Pr(Y|X)的条件分布，通过对数据概率生成机制的理解与建模进而获取良好的预测效果，这个过程会涉及X,Y,ϵX,Y,ϵ的分布假设，因此最后会衍生出对参数假设和误差分布的假设检验，以验证整个概率分布的假设的正确性，比如经典的线性模型、非参数回归等模型，预测能力并不是其主要目的；
2. 而机器学习基本不会从概率分布的角度着手，虽然可能也会涉及X,YX,Y的分布假设，但目的就是学习到一个能够较好描述数据生成机制的函数ff，对误差的假设基本忽略，也不会涉及参数和误差的检验，模型好坏基本由预测效果来判断，同时也会提供一些比较一般的误差上界，所以机器学习中不会出现参数估计渐进性、一致性等结果的讨论，而多半最终结果的评判。比如SVM、神经网络、KNN等模型。

不过即使有上述区别，关于高维统计推断（Lasso类带正则项的线性模型）的理论也逐渐完善，但相对于传统的生物制药、生物实验、社会调查、经济分析等领域，当前图像、文本、推荐系统等应用领域中，人们更关心模型的预测能力，而不是解释能力甚至是模型的可靠性，主要原因即这些领域模型预测能力相比于模型的假设检验要重要得多，因此如何根据模型预测能力来选择最优模型变得越来越重要。本文下面就逐步介绍模型选择的思路和方法，主要参考ELS这本书。

1. 偏移、方差、复杂度和模型选择

模型的预测能力通常也被称作模型的泛化能力，表示模型在新的、独立的测试数据上的预测能力。在很多关于模型泛化能力的介绍中，我们总会看到这样一幅图：模型在训练集上的训练误差与在测试集上的测试误差的变化趋势对比。

 

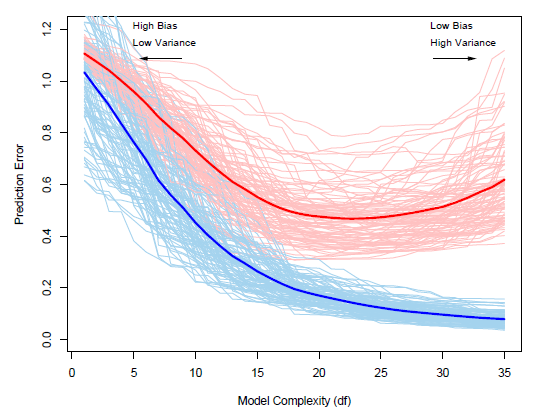图上横轴表示模型的复杂度大小（比如线性模型中特征维度大小），纵轴表示预测误差，衡量预测值与真实值间的平均损失大小E(L(Y,f^(X)))E(L(Y,f^(X)))，损失函数根据分类、回归问题做合适的选择，比如0-1损失、负似然函数、平方损失、对数损失、指数损失、交叉熵损失、Hinge损失等。平均损失大小在训练集上预测误差称作训练误差，在测试集上称作测试误差。图中每一条线都表示同一个训练集（浅蓝色）和测试集（浅红色）上的预测误差表现，从图上可以看到两个现象

• 训练误差（浅蓝色）和测试误差（浅红色）都有波动，并不是一个稳定的值，并且随着模型复杂度的增加，训练误差（浅蓝色）波动越来越小，而测试误差（浅红色）波动则越来越大；
•  随着模型复杂度增加，训练误差（浅蓝色）和平均训练误差（粗蓝线）越来越小，但测试误差（浅红色）和平均测试误差（粗红线）先降低后减小，在相对中间的位置有一个最小值。

看到这上面的现象，我们的脑中可能会冒出下面几个问题：

1. 为什么训练误差和测试误差会有波动？
2. 训练误差和测试误差的变化趋势说明了什么问题？
3. 造成这种变化趋势的原因是什么？
4. 这种趋势对模型的选择和评价有什么指导意义？

这四个问题由浅入深，最终目的就是想获取泛化能力最好和最稳定的预测模型。在回答这四个问题前，我们首先需要做一个假设：模型能够较好的预测，说明预测集与训练集有较好的相似性，更严格来说，很可能来源于同一分布，下文做分析时均假设来源于统一总体分布。如果测试集相对于训练集发生了巨大的变化，那么从训练到预测的思路将不可行。下面我们逐步来解答这四个问题。

1.1 为什么训练误差和测试误差会有波动？

现假设我们有个研究项目，想根据学生的平时表现和性格的pp个指标XX来预测最终该学生的期末综合成绩YY。为达到这个目的，我们在一个学校中我们随机抽了一批学生，选用某个模型训练，估计其模型参数，然后找一批新的学生预测来评价模型好坏，发现预测误差的相对误差非常小。但是通常人们会问，这个模型预测能力真的那么好么？我咋不相信根据学生平时表现和性格就可以得到这么好的预测效果呢？是不是你们特意挑选的一批学生呐？为了让他们相信这个模型还不赖，我们从这个学校重新抽了好几批学生，分别根据这些学生的指标去训练模型和估计模型参数。随后我们发现，换了几批学生样本，估计的模型参数确实有些差别，而且预测效果也是时好时坏，整体而言，平均的预测误差也还差强人意，能够控制预测误差的相对误差在20%以内，此时再把结果拿给其他人看，估计很多人对你的模型可能就不会有那么大疑问了。

对应到上文的图，其实上图的波动产生的原因也和该例子操作是一样的，有多条线就意味着重复抽了多组训练集来分别训练，因此训练误差和测试误差的波动是由训练样本的变化带来的。在理想的实验条件下，为了能公正地衡量模型的预测能力，通常需要多换几组训练集和测试集来综合评价模型的预测能力，这样的结果才可能让人更信服模型的预测能力，而不是偶然结果。

但是实际情况中，我们却可能仅有一个训练集和一个测试集。用数学化语言描述，新的测试集中，目标变量Y0Y0和预测变量X0X0均从两者的联合分布中抽取，独立于训练集T=(X,Y)T=(X,Y)，此时我们获取的测试误差（泛化误差）为某个训练集TT上测试集上损失的条件期望

 

ErrT=EX0,Y0(L(Y0,f^(X0))|T)ErrT=EX0,Y0(L(Y0,f^(X0))|T)

 

这里训练集TT是固定的，即仅有一个训练集。而从统计分析（重复试验）上来说，我们可能更关注测试误差的期望，即去掉训练集随机性所带来的影响：

 

Err=E(L(Y0,f^(X0)))=ET[ErrT]Err=E(L(Y0,f^(X0)))=ET[ErrT]

 

这个目标即上图预测误差波动想要表达的含义，想要通过多个训练集训练来获取平均的预测误差，抹平训练集变动带来的影响，这是评价模型预测能力最理想方法，可以防止某个训练集上训练所得模型表现过好而夸大模型的预测能力。但是实际情况中，我们手边通常可能只有一个训练集，实际的需求是在此训练集上模型做到最好，所以ErrTErrT又是我们最关心的目标，即希望在当前训练集下获取最佳的预测能力，也就是说我们想获取上图的一条线的趋势中最小的测试误差的点，如下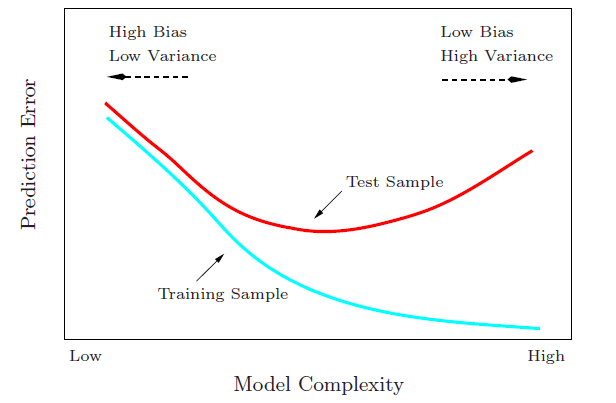

换句话说，很多时候人们给你一个训练集就希望你能够给他一个相对最稳定的预测模型，这个目标相对获取平均预测误差来说更难，后续模型选择方法比如CV法、bootstrap法、Cp法等其实都是估计测试误差的期望，即第一幅图中的红色均线。

1.2 训练误差和测试误差的变化趋势说明了什么问题？

图上反映的两个现象一句话表示即：随着模型复杂度增加，训练误差波动降低，平均训练误差降低趋向于0，而测试误差波动上升，平均测试误差先降低后升高。这个现象说明训练误差不能代替测试误差来作为模型选择和评价的手段。随着模型复杂度变化，训练误差与测试误差并不是一个良好的正相关关系，而是呈现较为复杂的非线性关系。用数学式子表示即

 

ErrTerr¯≠df→∞ConstErrTerr¯≠df→∞Const

 

用更通俗的话说，复杂的模型可能在训练集上拟合的很好，但是面对新的测试集，预测误差不降反升，发生了所谓的“过拟合”现象。如果一个模型在不同的测试集上测试结果不仅波动性大，而且预测误差也比较大，就要警惕发生了过拟合现象，此时不妨将模型的复杂度降低些（关于模型的复杂度含义下文会做更细致的说明），即使用变量更少的简单模型，比如线性模型。

过拟合的原因有很多，其中一个很可能的原因是，随着模型复杂度升高，对于训练数据刻画的很细，但是训练数据中可能某些特征仅出现过一次或者很少，信息不足，而测试集中该特征却出现了很多其他的值，虽然模型在训练集上刻画的足够细致，但是由于测试集的变动，模型反而往测试机上的迁移性能下降，训练误差变化并不正比于测试误差。

1.3 造成预测误差变化趋势的原因是什么？

那究竟是什么原因导致了随着模型复杂度增加，训练误差与测试误差不呈现良好的正比关系呢？为何同样都是预测误差，训练误差很小的模型反而预测能力很差呢？下面我们以线性模型为例来阐释原因，假设

y=f(x)+ϵ,E(ϵ)=0,Var(ϵ)=σ2ϵy=f(x)+ϵ,E(ϵ)=0,Var(ϵ)=σϵ2

 

如果用线性函数fp(x)=xTβfp(x)=xTβ去近似f(x)f(x)，其中pp表示特征个数，损失函数取平方损失，最小化1N∑i(yi–xTiβ)21N∑i(yi–xiTβ)2，则在训练集T=(X,Y)T=(X,Y)下得到参数估计为β^β^，同时记β∗β∗是f(x)f(x)最佳线性近似的估计参数

β∗=argminβEX(f(X)–XTβ)2β∗=arg⁡minβEX(f(X)–XTβ)2

 

在某个新样本点X=x0X=x0处预测误差为

Err(x0)==E[(y0–f^p(x0))2|X=x0]σ2ϵIrreducibleError+[f(x0)–Ef^p(x0)]2Bias2+E[Ef^p(x0)−f^p(x0)]2VarianceErr(x0)=E[(y0–f^p(x0))2|X=x0]=σϵ2⏟IrreducibleError+[f(x0)–Ef^p(x0)]2⏟Bias2+E[Ef^p(x0)−f^p(x0)]2⏟Variance

 

如果x0x0此时取所有训练集中的xixi，则其平均预测误差（该误差也被称作样本内(in-sample)误差，因为x0x0都是来自与训练样本内。不过y0y0都是新的观测，且真实的f(xi)f(xi)仍未知，因此该预测误差不是训练误差，后续会AIC等准则中会详细讲解）：

 

1N∑i=1NErr(xi)==σ2ϵIrreducibleError+1N∑i=1N[f(xi)–Ef^(xi)]2Ave(Bias2)+pNσ2ϵVarianceσ2ϵIrreducibleError+1N∑i=1N[f(xi)–xTiβ∗]2Ave[ModelBias]2+1N∑i=1N[xTiβ∗–ExTiβ^]Ave[EstimationBias]2+pNσ2ϵVariance1N∑i=1NErr(xi)=σϵ2⏟IrreducibleError+1N∑i=1N[f(xi)–Ef^(xi)]2⏟Ave(Bias2)+pNσϵ2⏟Variance=σϵ2⏟IrreducibleError+1N∑i=1N[f(xi)–xiTβ∗]2⏟Ave[ModelBias]2+1N∑i=1N[xiTβ∗–ExiTβ^]⏟Ave[EstimationBias]2+pNσϵ2⏟Variance

 

对于普通线性模型易知其“估计偏移（Estimation Bias）”为0（最小二乘估计也是线性估计类中的最佳估计），易知随着特征个数pp增加，方差（注：第一个等式根据线性回归很容易推导方差（Variance）为pNσ2ϵpNσϵ2）逐步增大，而对于真实f(X)f(X)却近似越好，模型偏误（Model Bias）越小，但预测误差是这两者的综合，则整体变化趋势如下图

这与上图测试集误差变化一致。另外，之所以特地提到还有“估计偏移”，因为对于线性模型类，还有其他诸如岭回归、Lasso等受限的回归类别，他们都属于线性模型类，相比纯线性模型，他们由于对回归系数做了不同程度的压缩，因此相比于最佳线性估计β∗β∗会有些差距，产生“估计偏移”，进而整体上导致“模型偏移”增加，但是他们限制了参数个数和压缩了回归系数，模型可能更加简单，因此直观上这类模型估计平均而言会稳定些（模型方差小），用图形来表示他们的关系即如下图

箭头组合长短即表示了平均预测误差，可以看到在受限模型空间中由于较小的模型估计方差，可能使得整体的平均预测误差更小。

1.4 对模型选择和评价有什么指导意义？

从“偏移-方差”分解可以看到，在有限的模型空间中，对某个模型类控制好模型的复杂度非常重要，否则不容易获取较好（包含稳定与预测误差小两方面）的预测模型，这便是模型选择阶段的工作。可能不少人觉得此处获取较好模型是指模型评价，但是模型评价与模型选择是两个不同的概念，代表两个不同的阶段：

• 模型选择：根据一组不同复杂度的模型表现，即从某个模型空间中挑选最好的模型；
•  模型评价：选择一个（最好）模型后，在新的数据上来评价其预测误差等评价指标。

从定义看，两者的目标不同，模型评价是模型选择的后一步。换句话说，模型选择是在某个模型类中选择最好的模型，而模型评价对这个最好的模型进行评价。模型评价可以比较多个模型类中的最佳模型，然后从中挑选出最佳模型，亦或者进行模型融合再进行评价。在模型选择阶段，常见的指标有AIC准则、BIC准则、CV值、结构风险上界等比较普适的准则，而在模型评价阶段，我们可以根据分类、回归、排序等不同问题关心的问题选择不同的评价指标，多与模型选择时的损失不同：（1）分类：ROC、AUC、TPR、FPR、F1 score；（2）排序：DCG、NDCG；（3）回归：RMSE、MAE、Deviance。根据具体业务，实际的评价指标有很多种，最好的方式当然是模型选择时即设计其损失函数即为评价指标，但是通常而言这些指标包含了某些非线性变化，优化起来难度颇大，因此实际模型选择仍是选用经典的那些损失函数，而模型评价则会与其略有不同。

随着机器学习普及，大家都有了“训练-验证-评价”的思维，这其实就是完整重现模型选择、模型评价的过程。如下图我们将数据集分成三个不相交的集合来做模型选择和模型评价：

• 训练集：获得模型及其训练误差，用来训练不同模型；
• 验证集：与训练集相对独立，获取训练模型在该集上的预测误差，用来做模型选择；
• 测试集：与训练集和验证集独立，获得真实的测试误差和其他模型评价指标，用来评价已选择出的模型。

使用训练集、验证集目的就是做模型选择，测试集自然是做模型评价。这三个集合的划分，并没有严格的准则，根据样本大小不同而做不同的选择，但是一个原则是测试集需要保持未知和与训练集、验证集的独立性。在数据挖掘比赛的时候，主办方通常会给我们一个训练集，然后自己持有一个未知的测试集。实际上这个测试集并不是真正的“测试集”，更应该称作“验证集”。因为随着参赛选手不断提交结果，他们在这个数据集也做了很多探索和尝试，能够逐渐发现这个所谓的“测试集”上的规律，模型选择和模型评价都依赖该数据集进行调整，因此从模型评价的独立性角度来说，这并不能当做最终的测试集，往往会低估预测误差，最好的做法是重新更换几组未知的数据集来当做新的“测试集”做模型评价，这也是秉承统计随机的思想——仅仅在某个“测试集”好是不够的（最近ImageNet事件也确实存在这样的问题）。

所以结合文章开始的方差-偏移图，对模型选择和模型评价的指导可以凝缩为一句话：根据已知的训练集和验证集在特定模型空间中进行模型选择，获取合适复杂度的模型，然后在多种模型空间做模型选择获取多种模型，最后的最优模型需要通过多个独立未知的测试集来做模型评价决定，否则很容易导致模型过拟合。（这实际上就是一个完整而规范的机器学习过程。）

2. 模型选择的方法

模型选择核心思想就是从某个模型类中选择最佳模型。注意，它与一般的“调参”意义不同，调参很多时候可能是针对优化算法中的某些参数进行调整，比如步长（学习速率）、mini-batch大小、迭代次数等，也会涉及到模型f(x,α)f(x,α)中调整参数（也称正则参数）αα的选择，但是模型选择不涉及算法中的参数，仅涉及模型目标函数中的调整参数αα。

从上面叙述可得知模型选择阶段，最标准的方法自然在训练集T=(X,Y)T=(X,Y)上训练模型，然后在验证集上获取预测误差ErrT=EX0,Y0(L(Y0,f^(X0))|T)ErrT=EX0,Y0(L(Y0,f^(X0))|T)，该误差也被称作“样本外（extra-sample）误差”，可真实反映出模型的样本外的预测能力，最后选择最小预测误差所对应的模型作为最佳模型即可。但通常而言，独立的验证集我们也没有，手头仅有的信息就是训练集，那么要想估计测试误差或者其期望曲线，就只能在训练集上做文章，一般而言可能仅有两种思路：

1. 从训练集划分点数据出来形成验证集来近似测试误差；
2. 对训练误差进行某种转化来近似测试误差。

第一种思路是非常自然的思路，只要对训练集进行合适的划分，我们就有可能近似出预测误差ErrTErrT。但是对原始训练集TT划分为新的训练集TnewTnew和验证集，不同的划分比例可能使得新训练集与原训练集相差较大，进而使得ErrTErrT差异很大，因此用这种划分的方式来估计条件期望形式的预测误差ErrTErrT比较困难。那么此时我们可以不估计ErrTErrT转为估计其期望，即平均预测误差ErrErr，通过重复抽样的方式来多次估计预测误差ErrTErrT，然后取其平均即可，这种方式我们可以称其为“重复抽样法”：通过训练集多次切分、抽样来模拟训练集、验证集，计算多个“样本外误差”，然后求其平均预测误差，这是一种密集计算型方法，比如交叉验证（Cross Validation）、自助法（bootstrap）等。

第二种思路相比第一种思路更加考虑计算效率，因为重复抽样需要计算多次估计，因此做一次模型选择可能需要花费不少时间，如果单单从训练集的训练误差就可以近似出测试误差ErrTErrT，那么模型选择效率便会大大提高。这种方式以统计学中的AIC、BIC等为代表，深刻剖析训练误差与之前提到的“样本内（in-sample）误差”、预测误差ErrTErrT间的关系，给出了预测误差估计的解析式，因此第二种思路我们可以称之为“解析法”。

这两种思路在统计学习和机器学习中都有大量应用，相比较而言，统计学习更喜欢第二种解析法，这样容易计算，并且会较好的理论性质（似然角度）；而机器学习则更喜欢第二种重复抽样法和从VC维衍生出来的结构风险最小化法，不需要计算基于分布的似然，普适性更好。

一般而言模型选择准则有如下几种：

• 重复抽样与预测稳定性角度：CV、GCV、Boostrap
• 似然与模型复杂度角度：AIC、AICc、BIC、EBIC
• VC维与风险上界控制角度：SRM

首先我们从更加普适的重复抽样法入手来介绍这些模型选择的方法和思路。

 2.1 重复抽样思路

CV法

交叉验证法（CV法）是最自然的重复抽样法，过程如下图所示

将一个训练集随机分成K份（图中所示为5份），然后选择第K份作为验证集（图中为第3份），然后剩余的K-1份作为训练集训练模型，这样便可以得到K个“预测误差”，求其平均值即为所谓的“CV值”，所以常说的CV值实际上是预测误差期望ErrErr的一个估计值。数学语言叙述如下：记τ:{1,…,N}→{1,…,K}τ:{1,…,N}→{1,…,K}是一个划分函数，表示随机地将第ii个观测分配{1,…,K}{1,…,K}中某个指标；记f^−k(x)f^−k(x)表示去除第kk部分数据训练所得的模型，则预测误差的交叉验证估计（CV值）为

 

CV(f^)=1N∑i=1NL(yi,f^−τ(i)(xi))CV(f^)=1N∑i=1NL(yi,f^−τ(i)(xi))

 

如果该模型有调整参数αα来调整模型的复杂度，记该模型集为f(x,α)f(x,α)，则CV值为

CV(f^,α)=1N∑i=1NL(yi,f^−τ(i)(xi,α))CV(f^,α)=1N∑i=1NL(yi,f^−τ(i)(xi,α))

 

此时通过调整参数αα可以获得不同模型复杂度下的CV值，然后选择最小的CV时所对应的模型f^(x,αcv−min)f^(x,αcv−min)作为最后的预测模型即可，这便是利用CV值来做模型选择的思路。

从CV估计定义可以看到，划分的份数KK粒度大小不同时，CV值对平均预测误差ErrErr的估计也有好坏之分，这里将涉及“偏误”、“方差”以及“计算效率”的权衡，主要是“偏误”与“计算效率”的权衡。以两个极端例子为例：

• K=NK=N时即“留一法（Leave-One-Out, LOO）”，表示每次切分的验证集仅为一个观测，其余的都是训练集，此时新训练集与原始训练集非常接近，则所得的CV值是平均预测误差的近似无偏估计，但是由于这N个训练集相关性也很高，训练的模型则也很相似，而且每次仅评价了一个观测，使得每个验证集上的预测误差相差较大，CV估计的方差较大，另外，N折交叉验证要估计N个模型，计算消耗巨大导致模型选择很慢；
• 如果KK取得较小，比如2，相当于一半数据用来训练一半用来验证，很显然此时新训练集与原始训练集差异较大，则CV值相对于真实平均预测误差会有较大偏误，导致会高估了平均预测误差，不过两个新训练集完全独立，训练出来的两个模型相关性很低，而且验证集数据比较充足，模型评价相对充分，在数据分布没有太大变化的大前提下，两个验证集上的预测误差会比较接近，使得CV估计的方差比较小，而此时计算消耗很少，模型选择效率高。

实际中，训练集切分带来的估计偏误与计算量才是我们真正关心的量。权衡偏误与效率的得失，由于CV对于预测误差的估计与训练样本大小有关，如果本身样本量就不大，交叉验证切分将导致训练样本更少，这会引起更大的估计偏差，所以实际折数KK经验是：

• 样本量大时，5折交叉验证对预测误差估计便足够，并且计算快速；
• 样本量小时，10折甚至LOO都可以，在损失计算效率的情况下优先考虑预测误差估计的准确性。

另外，由于5折或者10折CV估计有偏误，实际模型选择中还使用“one standard error”规则，即不选择CV值最小的模型，而是选择高于最小CV值一个标准差之内的最简模型，比如glmnet通常推荐lambda.1se，即这个准则。原因仍是5或10折CV很可能会低估平均测试误差，所以要保守选择平均预测误差略高于最小CV值得简单模型。

对于交叉验证法的实际操作，我们多半可能还会涉及变量筛选等预处理。对于这类预处理步骤，如果后续使用CV来做模型选择便需要考虑使用顺序的问题，一个使用原则是：

• 如果预处理涉及联合使用自变量XX与YY的关系，比如利用XX与YY的相关性等有监督方式来做变量选择，则需要在预处理前就需要对数据进行切分，数据预处理成了模型选择的一部分，而不能先变量筛选，然后在新数据进行交叉验证来做模型选择；
• 如果预处理不涉及自变量XX与YY的关系，仅仅利用XX自身的信息，比如XX的方差或者熵来做变量选择，这种无监督方式的预处理无需对数据进行切分来交叉验证，可以直接先无监督预处理完再利用交叉验证方法来做模型选择。

目前变量筛选的方法有很多，传统的有监督包含相关性筛选、熵增筛选等都是有监督方法，由于这种筛选已经利用了全体XX和YY间的关系信息，如果利用这种筛选后的数据来做交叉验证将会导致模型低估预测误差，高估了模型的泛化效果，因此实际使用时尤其需要注意这种筛选方法与交叉验证的联合使用，防止犯错。

另外，在分类问题中，特别是对于类别不平衡问题，由于CV法可能会导致每折中的类分布不一致，使得训练不稳定，因此实际中分层CV（stratified CV）也会使用。其相比较CV的不同之处就是不使用经典CV的均匀随机抽样方法来切分样本，而是根据总体类别比例，对每折都使用依赖于类别比例的分层抽样，保证每折的类别分布与原始数据差不多。学习过分层抽样的同学可能知道，分层抽样可以降低估计量方差，因此实际使用分层CV相比经典CV选择模型可能更稳定些。

GCV

由于计算CV是一个密集计算的模型选择法，即使可以利用并行计算来提高模型选择的效率，但是如果能够找到无需重复计算的替代方法，那么实际应用中，人们可能更倾向于使用这种模型选择方法。对于线性模型，如果使用平方损失，广义交叉验证（GCV）是LOO法解析形式的近似估计，可以避免计算N个模型来快速做模型选择。对于线性模型，对于目标变量的估计可以写成如下投影形式

y^=Syy^=Sy

其中SS是投影阵，仅与XX有关，与yy无关，则线性模型的LOO值为

1N(yi–f^−i(xi))2=1N∑i=1N(yi–f^(x)1–Sii)1N(yi–f^−i(xi))2=1N∑i=1N(yi–f^(x)1–Sii)

 

其中SiiSii是SS的对角元素，则GCV近似为

GCV(f^)=1N∑i=1N(yi–f^(x)1–trace(S)/N)GCV(f^)=1N∑i=1N(yi–f^(x)1–trace(S)/N)

此时不需要重复计算，只需要计算线性模型的投影阵SS的迹（后面也称作**自由度**）即可，极大降低了交叉验证的计算量，并且使得平均预测误差偏误更小，关于线性模型的GCV详细推导可参考此处。不过GCV仅适用于线性模型，包含带正则项的普通线性模型、非参线性模型，比如LASSO、岭回归、样条回归、多项式回归等模型，其余比如树模型、神经网络模型都不适合。

 

关于CV的衍生方法比较新的时ES-CV，由Yu Bin在2013年提出，不过实际上这种方法对于核心是估计稳定性的定义，CV法只是来改进估计稳定性的一种方式而已，感兴趣的同学可以参考Yu老师的论文。

 Bootstrap法

对于bootstrap，不管是统计还是机器学习的同学，可能对这个名词以及实施方式都比较熟悉。bootstrap法由Efron于1979年提出，随后在统计中得到了大量的应用，主要用于解决复杂统计量的置信区间等估计问题；而在机器学习中，由Breiman在94年提出bagging方法（全称为bootstrap aggregating）实际上就是bootstrap的直接应用，它是一种模型组合方法，主要用于分类问题中以获取比较稳定的结果。bootstrap的思路和操作都非常简单，如下图

假设有样本ZZ，则不断重复随机抽同样大小的B个样本集Z∗bZ∗b，这些样本被称作bootstrap样本，随后用着B个样本分别训练模型，得到B个目标估计量S(Z∗b)S(Z∗b)。然后可以用这些统计量求某些指标，比如统计量的均值、方差、偏移等。对于分类问题，用这些bootstrap样本训练多个分类器，比如决策树或神经网络，然后将这B个分类模型对新的样本做预测，把B个分类结果做一个投票获取最终的结果即可，这边是所谓的bagging。

不过上述都是对于估计量或者模型而言，那么如何利用bootstrap来做模型选择呢？如果我们用着B个模型对每个观测都进行评价，然后求其平均误差

 

Err^boot(α)=1B1N∑b=1B∑i=1NL(yi,y^∗b(xi,α))Err^boot(α)=1B1N∑b=1B∑i=1NL(yi,y^∗b(xi,α))

 

看起来似乎可行，但仔细一思考就可以发现这并不是一个好的平均预测误差的估计，主要原因是bootstrap样本即被训练又被评价，与CV不同训练集被重复分割为独立的训练集与验证集相比，数据评价存在重合，所以Errboot(α)Errboot(α)肯定与训练误差可能比较接近，而与平均预测误差有较大偏差，那么用该估计来调模型复杂度参数αα显然更不是个好选择。那如何利用bootstrap法来更好的近似平均预测误差呢？我们可以借助于CV的分割思想。

我们知道，bootstrap样本的获取其实就是重复有放回的N次抽样，那么对于观测ii属于该bootstrap样本，至少被抽中一次的概率即

 

Pboot=1–(1–1N)N⟶N→∞1–1/e∼0.632Pboot=1–(1–1N)N⟶N→∞1–1/e∼0.632

 

换句话说，每个bootstrap样本中，总有些观测没被抽到，那么根据CV法的思路，这部分观测就可以拿出来作为验证集来作为平均预测误差的估计。
熟悉随机森林或者Bagging的同学对于OOB（out of bag）这个词肯定不陌生。OOB其实就是这种思路，不过只是对未抽中的样本再次做了投票然后再估计预测误差，对于此处我们则不做投票，直接取那些没出现过ii观测的bootstrap样本训练的模型分别估计ii的误差，然后求个平均即可

 

Err^(1)boot(α)=1N∑i=1N1C−i∑b∈C−iL(yi,f^∗b(xi,α))Err^boot(1)(α)=1N∑i=1N1C−i∑b∈C−iL(yi,f^∗b(xi,α))

 

其中C−iC−i即不包含ii观测的bootstrap样本集。你可能想万一有个观测所有bootstrap都出现了怎么办？直接去掉就好了嘛，不过你可以算算B个bootstrap样本都出现的概率有多小。实际而言，B大点便很容易保证观测ii很难在所有bootstrap样本集中出现了。

下面在思考下，这种估计是对平均预测误差估计是个好估计吗？虽然不会像第一个估计量那样低估平均预测误差，但是这种估计量也很容易高估平均预测误差，主要原因是每个bootstrap样本中仅有差不多63.2%的不同观测用来建模，这样使得Err^(1)boot(α)Err^boot(1)(α)估计量表现得很像2折或3折交叉验证，分割太少导致可能偏差很大，特别是对于样本量不够多的训练集。如果改进，直观想法便是将训练误差ErrtrainErrtrain与该估计量Err^(1)boot(α)Err^boot(1)(α)按照某种比例加权(1–w)Errtrain+wErr^(1)boot(α)(1–w)Errtrain+wErr^boot(1)(α)来纠正这种偏移，具体细节可以看ESL的阐述，实际中由于bootstrap计算量过大，所以用来做模型选择不多，所以此处不再详述。

不过在大数据时代，分布式思维逐深入统计学家和计算机学家脑中，由于bootstrap具备良好的可并行性，以及良好的统计性质和估计稳定性，Jordan在2012便提出了基于bootstrap的[BLB(Bag of Little Bootstraps)](http://arxiv.org/pdf/1112.5016v2.pdf)，能够给出较稳定的估计量以及估计量的区间估计，这是其他方法不具备的特点。比如能告诉你预测误差大小，同时可以告诉你预测误差的偏误以及方差，那这是不是一件更令人安心的事情呢？在现在这种环境下，与其不停做实验等待结果，不妨考虑下bootstrap这类有可靠性估计的方法的好处。BLB的算法思路很清晰，简单来说：subsampling + bootstrap + average；先无放回抽样，然后bootstrap抽样，获取参数bootstrap估计量，以及其置信区间、偏移、预测误差等估计量，最后将这些估计量平均起来即可。细节可以参考其论文，只要有多机可并行环境便可很容易实施该方法。

bootstrap思想是一种非常重要思想，后来著名的random forest便充分利用了该思路。而且相比目前的数据并行、模型并行的分布式算法思路，我觉得可以从bootstrap抽样角度获取更加稳定的估计量，当然这些都是题外话，与本文话题不相符合，以后可以再谈谈抽样与并行算法之间的感想，实际上都会在“计算效率”与“精度”之间做些权衡。

2.2 解析解思路

根据上述重复抽样法可知，CV等方法直接来估计“样本外误差”，并求其期望，而解析解思路由于不像CV法通过原始训练集切分构建验证集，仅仅从训练集出发，构建训练误差与“样本内误差”间等式关系，因此需要深刻理解训练误差、“样本内误差”、模型复杂度这几个概念，才能较好的理解为何解析解思路的那几个准则是有效的。

2.2.1 训练误差与样本内误差

在本文第一节提到，实际应用中通常只有一个训练集T={(x1y1),…,(xn,yn)}T={(x1y1),…,(xn,yn)}，此时我们希望能在该训练样本上获得最好的预测模型f^f^，在新样本点(X0,Y0)(X0,Y0)能得到最小的泛化误差ErrT=EX0,Y0[L(Y0,f^(X0))|T]ErrT=EX0,Y0[L(Y0,f^(X0))|T]。这是训练集TT上预测误差的条件期望，随着样本集变动而变动。但从统计角度来说，抹掉训练集带来的变动，估计预测误差的期望更符合统计口味Err=ETEX0,Y0[L(Y0,f^(X0))|T]Err=ETEX0,Y0[L(Y0,f^(X0))|T]，这也是上述CV、bootstrap采取的方式。

在第一部分关于err¯err¯和ErrTErrT与模型复杂度走势的图形中，可以看到err¯err¯低估了ErrTErrT，并且复杂度高的模型容易过拟合，导致errerr很小，而ErrTErrT很大，所以用err¯err¯来评测模型就显得过于乐观了。但是，能不能建立err¯err¯与ErrTErrT间的关系呢？

由于ErrTErrT要引入新X0,Y0X0,Y0有难度，那么退一步看XX不变动而仅引入新的Y0Y0的预测误差

Errin=1N∑i=1NEY0i[L(Y0i,f^(xi))|T]Errin=1N∑i=1NEYi0[L(Yi0,f^(xi))|T]

这种误差称作“样本内误差”（in-sample误差），虽然也是一种预测误差，但是XX没有变动，因此对于模型泛化估计能力还是不够。不过样本内误差与样本外误差与模型复杂度的关系走势类似，对于模型选择而言，更关心误差的相对值而不是其绝对值，因此实际模型选择中，我们也常常关注“样本内误差”，它也是一种有效且更方便的思路，并且此时建立ErrinErrin与err¯err¯间的关系相对更容易了。

 

由于ErrinErrin与err¯err¯都拥有相同的XX，两者唯一的区别便是ErrinErrin是对YY求了期望，而err¯err¯则直接使用了某个YY值（训练样本），两者的差便是

 

op≡Errin–err¯op≡Errin–err¯

 

为更便于理解，以平方损失和线性模型为，且预测值y^y^是原始值yy的线性变换y^=Syy^=Sy，则

 

op≡1N∑i=1N[EY0i(Y0i–y^i)2–(yi–y^i)2)]op≡1N∑i=1N[EYi0(Yi0–y^i)2–(yi–y^i)2)]

与预测误差类似，这其实是关于训练样本点yiyi的条件期望，这种条件期望不好估计和分析，因此消除训练样本中yiyi变异带来的影响，我们再次对所有y={yi}Ni=1y={yi}i=1N求期望（注意这其中样本点与随机变量间概念的转化，此处将yiyi看做是样本点还是随机变量并不做严格区分，所以Eyiyi=EYiY0iEyiyi=EYiYi0）

 

 

ω≡Ey(op)≡1N∑i=1N[EyiEY0i(Y0i–y^i)2–Eyi(yi–y^i)2]=1N∑i=1N2(Eyi(yiy^i)–EyiyiEyiy^i)=2N∑i=1NCov(yi,y^i)ω≡Ey(op)≡1N∑i=1N[EyiEYi0(Yi0–y^i)2–Eyi(yi–y^i)2]=1N∑i=1N2(Eyi(yiy^i)–EyiyiEyiy^i)=2N∑i=1NCov(yi,y^i)

 

于是我们便得到了如下非常重要的关系式

Ey(Errin)=Ey(err¯)+2N∑i=1NCov(yi,y^i)Ey(Errin)=Ey(err¯)+2N∑i=1NCov(yi,y^i)

因此从消除训练集变动的影响（期望）角度来看，我们找到了训练误差与“样本内误差”间的数量关系，这个关系式推广到0-1损失或者似然形式都成立。对于加性误差的线性模型y=f(x)+ϵy=f(x)+ϵ，易知

∑i=1NCov(yi,y^i)=∑i=1NCov(yi,Syi)=trace(S)σ2ϵ=∑i=1Ndσ2ϵ∑i=1NCov(yi,y^i)=∑i=1NCov(yi,Syi)=trace(S)σϵ2=∑i=1Ndσϵ2

 

其中SS与dd便是线性模型的有效参数个数，也称作自由度，注意仅对于线性模型如此，控制着模型复杂度。可以看到，“样本内误差”与训练误差间的桥梁就是模型复杂度！当模型复杂度过高时，很可能“样本内误差”不降反升。

 2.2.2 Cp法与AIC

借助上述训练误差与样本内误差的关系式，实际中我们便可以这样来对“样本内误差”做这样的估计

Err^in=err¯+ω^Err^in=err¯+ω^

训练误差与“样本内误差”都不是期望形式，看起来有些混合，不过由于实际情况无法求yy的期望，所以我想这也是没办法的“最佳”估计了吧，统计中常会遇到这种知难而相对随意的形式- -!

 

对于平方损失下的线性模型（注意此时的损失限制），所谓的Cp准则即为

Cp=err¯+2⋅dNσ^2ϵCp=err¯+2⋅dNσ^ϵ2

其中σ2ϵσϵ2用包含所有变量的回归模型的残差估计所得。乍一看过去，这完全就是给“样本内误差”估计换了个名称而已嘛:)

 

AIC准则与之略有差异，训练误差选用似然函数的负数来代替，而ω^ω^没有噪音方差的估计σ^2ϵσ^ϵ2，为如下形式

AIC=−2N⋅loglike+2⋅dNAIC=−2N⋅loglike+2⋅dN

 

dd仍是模型的参数个数，用来衡量模型复杂度。对于非线性模型和更复杂的模型，此处dd需要用其他形式来代替。

对于误差为已知方差的高斯模型，化简似然函数便可知AIC就等价于Cp准则。对似然函数化简，可以得到对应的不同的各类损失，比如高斯模型与平方损失的对应，logistic模型与cross entropy损失的对应等，所以相比仅只适用于平方损失线性模型的Cp准则，AIC适用范围更广。实际使用中，AIC做模型选择更倾向于选择比真实模型更多参数的模型，容易低估“样本外误差”，有**过拟合的倾向**。

另外AIC准则还与KL距离有紧密联系，可以从KL距离来推出AIC准则，感兴趣的同学可以参考这篇文档中关于AIC的介绍。而关于AIC的校正版AICc准则，实际中也有使用，关于其介绍可直接参考wiki。

2.2.3 BIC与贝叶斯

BIC准则形式项与AIC很像，同样还是似然负数作为损失，然后加上一个关于自由度与样本相关的项。

BIC=−2⋅loglike+(logN)⋅dBIC=−2⋅loglike+(log⁡N)⋅d

对于方差已知的高斯模型，化简似然函数即可得

BIC=Nσ2ϵ[err¯+(logN)⋅dNσ2ϵ]BIC=Nσϵ2[err¯+(log⁡N)⋅dNσϵ2]

忽略比例项，此时BIC与Cp和AIC基本一致，只是第二项的因子2换成了logNlog⁡N，相比AIC和Cp准则，BIC对于参数更多、复杂度更高的模型惩罚更重。虽然看起来相似，但是BIC原始想法并不是类似AIC这种思路，而是从贝叶斯角度出发得到的。

 

从贝叶斯角度来看，模型选择无非就是依托于当前样本数据XX，从候选模型集合Mm,m=1,…,MMm,m=1,…,M中选择后验概率最大的模型即可（所谓后验概率即从数据反推可能模型的概率，MmMm可以看做是所有变量(1,…,p)(1,…,p)中得的某个变量子集），当然每个模型都有相应自己的参数θmθm，且这些参数也有先验概率分布P(θm|Mm)P(θm|Mm)，根据贝叶斯公式可知给定数据XX时模型后验概率为

P(Mm|X)=P(Mm)⋅P(X|Mm)P(X)∝P(Mm)⋅P(X|Mm)=P(Mm)⋅∫P(X|θm,Mm)P(θm|Mm)dθmP(Mm|X)=P(Mm)⋅P(X|Mm)P(X)∝P(Mm)⋅P(X|Mm)=P(Mm)⋅∫P(X|θm,Mm)P(θm|Mm)dθm

 

对于模型选择而言，我们并不需要作上述复杂的积分，只需要比较模型后验概率的相对大小即可，这样的好处是忽略常数项是的计算简便了很多

P(Mm|X)P(Ml|X)=P(Mm)P(Ml)⋅P(X|Mm)P(X|Ml)P(Mm|X)P(Ml|X)=P(Mm)P(Ml)⋅P(X|Mm)P(X|Ml)

具备最大后验概率的模型将与其他所有模型的后验概率比值都大于1。进一步，如果我们事先对模型情况一无所知，模型先验P(Mm)P(Mm)服从均匀分布均相等，那么寻找最大后验概率的模型就演变成了寻找最大概率密度P(X|Mm)P(X|Mm)的模型即可，实际上取对数即求最大似然logP(X|Mm)log⁡P(X|Mm)。由于θmθm被积分掉，求解P(X|Mm)P(X|Mm)很困难，所以实际中我们可以采用[Laplace近似](https://stat.duke.edu/~st118/sta250/laplace.pdf)即可，只要样本量足够大，该近似效果便很好，通过Laplace近似，似然logP(X|Mm)log⁡P(X|Mm)变成了

 

 

−BIC≈log(X|Mm)=logP(X|θ^m,Mm)–dm2⋅logN+O(1)−BIC≈log⁡(X|Mm)=log⁡P(X|θ^m,Mm)–dm2⋅log⁡N+O(1)

 

其中，θmθm为极大似然估计，dmdm为模型MmMm的自由参数个数。很显然，只需要将似然函数logP(X|θ^m,Mm)log⁡P(X|θ^m,Mm)作相应替换，去掉常数项，求解模型的最大后验概率就等价于最小化BIC，因此在样本量很大使得lalapce近似效果很好时，BIC准则便渐进选择最佳模型。

（注：一句话阐述Laplace技巧即，对于复杂概率函数的似然求解，我们可以将其在参数的极大似然估计处做二阶泰勒展开，根据似然函数在MLE估计处的一阶导为0的性质，原始的概率函数可凑成正态密度函数的形式，于是复杂概率函数就可以用均值和方差均可求的正态分布来近似。）

有了BIC值，我们也可以直接给出每个模型MmMm的后验概率

P(Mm|X)=exp(−12⋅BICm)∑Ml=1exp(−12⋅BICl)P(Mm|X)=exp⁡(−12⋅BICm)∑l=1Mexp⁡(−12⋅BICl)

这对于模型选择将更加直观，只是计算所有模型的BIC值计算量太大了，实际中我们多半不会如此操作。

 

虽然在样本量大且变量维数固定时，BIC准则有模型渐进一致性，但是面对实际有限的样本，BIC相比AIC的过拟合又会欠拟合，对模型复杂度控制太严格，导致选择相对过于简单的模型。另外，BIC在模型特征维度pp大时，估计模型更加会有偏差，因此关于BIC的改进版EBIC准则便应运而生。

EBIC法主要的改进思路是对模型先验分布P(Mm)P(Mm)的均匀分布进行合理改进。当变量维数比较大时，含不同变量数的模型个数是不同的，比如XX现为1000维变量,则包含1个变量的模型ss有1000个，模型集合即为S1S1，而包含2个变量的模型ss有1000×999/21000×999/2，模型集合记为S2S2，可以看到S2S2的大小将近是S1S1的500倍。按照BIC的均匀分布假设，所有模型ss被选择概率相同P(s)=1/MP(s)=1/M，这将导致P(Sj)P(Sj)被选择的概率与之模型集合大小π(Sj)π(Sj)成正比，换句话说，差不多含一半变量数的Sp/2Sp/2模型集合中的模型ss被选择概率最大，这显然与变量数可能比较小（稀疏）的假设精神相违背，特别在更加高维的情况中，BIC将会更加倾向在较大的模型空间选择，导致选择的变量数过多。

为了改进这种所有BIC所有模型等同视之的思路，EBIC略作了改动，对于属于同一个模型集合SjSj的模型ss自然仍等同视之，概率为P(s|Sj)=1/π(Sj)P(s|Sj)=1/π(Sj)，但对于不同的模型集合SjSj整体的先验被选概率则与之大小πξ(Sj),0≤ξ≤1πξ(Sj),0≤ξ≤1成正比，而不是直接与其大小π(Sj)π(Sj)成正比，这种简单的幂次方式可以平滑不同大小的模型集合被选择的概率，使之差异不那么大，于是模型P(s)P(s)被选择的概率就正比于πγ(Sj),γ=1−ξπγ(Sj),γ=1−ξ，带入原来的推导式子，便可得到如下的EBIC准则

EBICγ=−logP(X|θ^m,Mm)+dm2⋅logN+γlogπ(S(Mm))EBICγ=−log⁡P(X|θ^m,Mm)+dm2⋅log⁡N+γlog⁡π(S(Mm))

 

其中S(Mm)S(Mm)表示MmMm所属的模型集合，模型集合中变量个数相同。所以EBIC相比于BIC增加的惩罚更大，一般经验是“**如果维度pp增长速度相比样本量为O(nk)O(nk), 若k<0.5k<0.5维度增长很慢，则EBIC0EBIC0即BIC准则下的模型选择具备一致性；而如果k<1k<1维度较快时，则EBIC0.5EBIC0.5模型选择具备一致性，只要pp不是随样本量nn指数级增长，kk接近1，则EBIC1EBIC1模型选择是一致的**”。实际建模中，考虑实际数据维度增加与样本增加的关系，选择合适的γγ即可，关于EBIC的论文和讲义可以分别参考这里和这里。

3. 总结

其他模型选择方法还有“最小描述长度（MDL）”和“基于VC维的最小结构风险法（VC-SRM）”。这两种方法一个从最优编码的角度，一个从数据可分性角度分别来阐述模型选择，感兴趣同学可以学习这两种思想，不过由于方法各有缺陷，实际应用较少。

总之，对于模型选择方法，实际中由于CV法、GCV法的通用性，不管在计算机还是统计领域中都大量应用。而其他的BIC等法则，由于计算快速且有良好的理论性质，统计领域的研究者可能更加喜欢这类方法。不过由于他们基于似然并不是通用框架，并且对于预测来说，根植于样本内误差做的模型选择，模型预测能力很可能不如预期，因此实际应用，我们也更加推荐CV法、GCV法来做模型选择，毕竟现在计算能力如此强大，并行处理也比较方便，而且方法也比较灵活，可以模型选择，也可以模型组合。通过学习这些方法，我们可以充分感受到不同学科的思考方式，通常而言，简单的方法会比较可靠，但是可能需要大量计算来验证、评价；而需要绕些脑子的方法，多半是为了能够进一步简化运算而推演的，这样可能会认识到更深刻的规律，但也可能会使用不少近似的方法来损失精度。对于现实计算而言，“效率-精度”总是一个绕不开的话题，以后有机会我们可以再谈谈这个问题。