机器学习中使用「正则化来防止过拟合」到底是一个什么原理？为什么正则化项就可以防止过拟合？
原文：http://www.zhihu.com/question/20700829
27 个回答
Orangeprince 的回答非常学院派，也非常系统。 过拟合表现在训练数据上的误差非常小，而在测试数据上误差反而增大。其原因一般是模型过于复杂，过分得去拟合数据的噪声和outliers. 正则化则是对模型参数添加先验，使得模型复杂度较小，对于噪声以及outliers的输入扰动相对较小。 以正则化项和损失函数都是l_2 norm 为例，下面贴一张上课用的slide.
我们相当于是给模型参数w 添加了一个协方差为1/alpha 的零均值高斯分布先验。 对于alpha =0，也就是不添加正则化约束，则相当于参数的高斯先验分布有着无穷大的协方差，那么这个先验约束则会非常弱，模型为了拟合所有的训练数据，w可以变得任意大不稳定。alpha越大，表明先验的高斯协方差越小，模型约稳定， 相对的variance也越小。
也正如其他答题者所说， 加入正则化是 在bias和variance之间做一个tradeoff.
我们相当于是给模型参数w 添加了一个协方差为1/alpha 的零均值高斯分布先验。 对于alpha =0，也就是不添加正则化约束，则相当于参数的高斯先验分布有着无穷大的协方差，那么这个先验约束则会非常弱，模型为了拟合所有的训练数据，w可以变得任意大不稳定。alpha越大，表明先验的高斯协方差越小，模型约稳定， 相对的variance也越小。 也正如其他答题者所说， 加入正则化是 在bias和variance之间做一个tradeoff.
一般的监督学习，大概可以抽象成这样的优化问题：
min loss( y - f(x) ) + \Omega ( f )
f()是你要学习的model，y是监督的target. 为了更直观的解释，上面的regulazed的形式也可以写成下面constrained的形式:
min loss(y - f(x)) s.t. \Omega(f) < \lambda
如果是最简单的线性回归模型，那么就是：
min || y - wX ||^2 s.t. ||w|| < \lambda, 这里面 ||w|| 越大，也就说明w向量离远点越远，模型的复杂程度越高，方法的bias越大，variance越小，也就会造成我们常说的过拟合。而一些非线性映射，或者KNN算法，则有着更高的模型复杂度。相反，\lambda越小，方法的bias也越小，能够更好地拟合训练数据，但是方法的variance更大， 输出变量于输出变量期望的差异也更大。
从概率的角度来说，对模型的正则化项其实就是对w给出一个先验的分布。如果正则化项和损失函数都是l_2 norm，其实就给了w一个期望是0，协方差矩阵是 \delta I的先验分布。之后计算w，就是在给定w的先验、x和y的情况下，用最大似然估计最大化w的后验概率，求出w的最优解。\lambda越大，表示w的先验分布的协方差越小，也就是w越稳定。其他的正则话项也可以对应其他的先验分布，比如l_1的正则话项对应Laplace先验。
min loss( y - f(x) ) + \Omega ( f )
f()是你要学习的model，y是监督的target. 为了更直观的解释，上面的regulazed的形式也可以写成下面constrained的形式:
min loss(y - f(x)) s.t. \Omega(f) < \lambda
如果是最简单的线性回归模型，那么就是：
min || y - wX ||^2 s.t. ||w|| < \lambda, 这里面 ||w|| 越大，也就说明w向量离远点越远，模型的复杂程度越高，方法的bias越大，variance越小，也就会造成我们常说的过拟合。而一些非线性映射，或者KNN算法，则有着更高的模型复杂度。相反，\lambda越小，方法的bias也越小，能够更好地拟合训练数据，但是方法的variance更大， 输出变量于输出变量期望的差异也更大。
从概率的角度来说，对模型的正则化项其实就是对w给出一个先验的分布。如果正则化项和损失函数都是l_2 norm，其实就给了w一个期望是0，协方差矩阵是 \delta I的先验分布。之后计算w，就是在给定w的先验、x和y的情况下，用最大似然估计最大化w的后验概率，求出w的最优解。\lambda越大，表示w的先验分布的协方差越小，也就是w越稳定。其他的正则话项也可以对应其他的先验分布，比如l_1的正则话项对应Laplace先验。
数学原理我不细说，google能得到一大坨解释，以及其他各位牛人也都回答了，奥坎姆剃刀这类概念我也不说，相信题主早就知道。我想你就差一个俗气的解释，那么我来几个俗气的解释。
解释之前，先说明这样做的目的：如果一个模型我们只打算对现有数据用一次就不再用了，那么正则化没必要了，因为我们没打算在将来他还有用，正则化的目的是为了让模型的生命更长久，把它扔到现实的数据海洋中活得好，活得久。
俗气的解释1：
让模型参数不要在优化的方向上纵欲过度。《红楼梦》里，贾瑞喜欢王熙凤得了相思病，病榻中得到一枚风月宝鉴，可以进入和心目中的女神XXOO，它脑子里的模型目标函数就是“最大化的爽”，所以他就反复去拟合这个目标，多次XXOO，于是人挂掉了，如果给他加一个正则化，让它爽，又要控制爽的频率，那么他可以爽得更久。
俗气的解释2：
假如马化腾心中的商业模型优化目标是让腾讯发展得更好，他的模型只有一个特征，就是张小龙，根据他的目标以及已有样本，它应该给张小龙赋予更大的权重，就可以一直让模型的表现朝这个目标前进，但是，突然有一天马化腾意识到：这样下去不行啊，他的权重大得没边的话，根本不可持续啊，他要是走了，他要是取代我了。于是马化腾就需要在优化这个目标的时候给这个唯一的特征加一个正则化参数，让权重不要过大，从而使得整个模型能够既朝着设定目标走，又不至于无法持续。
俗气的解释3：
我们这群技术男在公司里，如果模型目标是提高自身能力并最终能够在公司有一席之地，理想的优化方法是提高各种牛逼算法，各种高大上的计算平台的熟悉程度，尽量少开无谓的会议，少接领导扯淡的需求，但是如果只是这些的话，很可能在这个公司呆不太久，因为太关注自己的特征权重了，那么如果这个公司其实非常适合提升自己的能力，那么要能在这里呆久点，就得适当限制自己这些特征的权重绝对值，不要那么绝对坚持用到牛逼算法，偶尔也处理处理领导的扯淡需求，平衡一下，你的模型才能泛化得更广。
最后，我还是正本清源一下，正经再简单解释一下正则化，以下内容来自PRML前三章，具体页数记不清了。
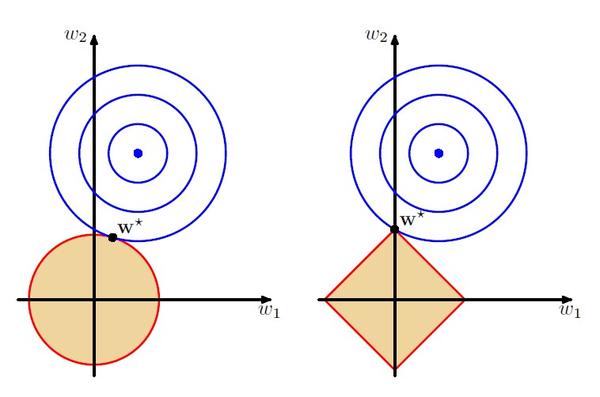
上图中的模型是线性回归，有两个特征，要优化的参数分别是w1和w2，左图的正则化是l2，右图是l1。蓝色线就是优化过程中遇到的等高线，一圈代表一个目标函数值，圆心就是样本观测值（假设一个样本），半径就是误差值，受限条件就是红色边界（就是正则化那部分），二者相交处，才是最优参数。可见右边的最优参数只可能在坐标轴上，所以就会出现0权重参数，使得模型稀疏。这个图告诉我们，如果你太绝对相信那个目标了，沉迷其中，那些还没遇到的样本一来，你拔不出来就挂掉了。
最后， regularize这个词更多的意思是“使系统化”，“使体系化”，也就是说不要走极端，要建立和谐社会，科学发展观。
==================================
再补充一个角度：
正则化其实就是对模型的参数设定一个先验，这是贝叶斯学派的观点，不过我觉得也可以一种理解。
L1正则是laplace先验，l2是高斯先验，分别由参数sigma确定。
求不要追究sigma是不是也有先验，那一路追究下去可以天荒地老。
解释之前，先说明这样做的目的：如果一个模型我们只打算对现有数据用一次就不再用了，那么正则化没必要了，因为我们没打算在将来他还有用，正则化的目的是为了让模型的生命更长久，把它扔到现实的数据海洋中活得好，活得久。
俗气的解释1：
让模型参数不要在优化的方向上纵欲过度。《红楼梦》里，贾瑞喜欢王熙凤得了相思病，病榻中得到一枚风月宝鉴，可以进入和心目中的女神XXOO，它脑子里的模型目标函数就是“最大化的爽”，所以他就反复去拟合这个目标，多次XXOO，于是人挂掉了，如果给他加一个正则化，让它爽，又要控制爽的频率，那么他可以爽得更久。
俗气的解释2：
假如马化腾心中的商业模型优化目标是让腾讯发展得更好，他的模型只有一个特征，就是张小龙，根据他的目标以及已有样本，它应该给张小龙赋予更大的权重，就可以一直让模型的表现朝这个目标前进，但是，突然有一天马化腾意识到：这样下去不行啊，他的权重大得没边的话，根本不可持续啊，他要是走了，他要是取代我了。于是马化腾就需要在优化这个目标的时候给这个唯一的特征加一个正则化参数，让权重不要过大，从而使得整个模型能够既朝着设定目标走，又不至于无法持续。
俗气的解释3：
我们这群技术男在公司里，如果模型目标是提高自身能力并最终能够在公司有一席之地，理想的优化方法是提高各种牛逼算法，各种高大上的计算平台的熟悉程度，尽量少开无谓的会议，少接领导扯淡的需求，但是如果只是这些的话，很可能在这个公司呆不太久，因为太关注自己的特征权重了，那么如果这个公司其实非常适合提升自己的能力，那么要能在这里呆久点，就得适当限制自己这些特征的权重绝对值，不要那么绝对坚持用到牛逼算法，偶尔也处理处理领导的扯淡需求，平衡一下，你的模型才能泛化得更广。
最后，我还是正本清源一下，正经再简单解释一下正则化，以下内容来自PRML前三章，具体页数记不清了。
上图中的模型是线性回归，有两个特征，要优化的参数分别是w1和w2，左图的正则化是l2，右图是l1。蓝色线就是优化过程中遇到的等高线，一圈代表一个目标函数值，圆心就是样本观测值（假设一个样本），半径就是误差值，受限条件就是红色边界（就是正则化那部分），二者相交处，才是最优参数。可见右边的最优参数只可能在坐标轴上，所以就会出现0权重参数，使得模型稀疏。这个图告诉我们，如果你太绝对相信那个目标了，沉迷其中，那些还没遇到的样本一来，你拔不出来就挂掉了。
最后， regularize这个词更多的意思是“使系统化”，“使体系化”，也就是说不要走极端，要建立和谐社会，科学发展观。
==================================
再补充一个角度：
正则化其实就是对模型的参数设定一个先验，这是贝叶斯学派的观点，不过我觉得也可以一种理解。
L1正则是laplace先验，l2是高斯先验，分别由参数sigma确定。
求不要追究sigma是不是也有先验，那一路追究下去可以天荒地老。
过拟合的时候，拟合函数的系数往往非常大，而正则化是通过约束参数的范数使其不要太大，所以可以在一定程度上减少过拟合情况。
2013.12.3 补充：
说说为什么过拟合的时候系数会很大。
如下图所示，过拟合，就是拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大。在某些很小的区间里，函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值（绝对值）非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大。
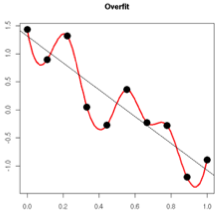
2013.12.3 补充：
说说为什么过拟合的时候系数会很大。
如下图所示，过拟合，就是拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大。在某些很小的区间里，函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值（绝对值）非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大。
最简单的解释就是加了先验。在数据少的时候，先验知识可以防止过拟合。
举2个例子：
1. 抛硬币，推断正面朝上的概率。如果只能抛5次，很可能5次全正面朝上，这样你就得出错误的结论：正面朝上的概率是1--------过拟合！如果你在模型里加正面朝上概率是0.5的先验，结果就不会那么离谱。这其实就是正则。
2. 最小二乘回归问题：加2范数正则等价于加了高斯分布的先验，加1范数正则相当于加拉普拉斯分布先验。
----------------------
拿Lasso（1范数正则）举例
其实就是如下概率模型的最大后验。
如果不对w加拉普拉斯分布的先验，最大后验得到的是
其实正则项就是对w的先验分布
举2个例子：
1. 抛硬币，推断正面朝上的概率。如果只能抛5次，很可能5次全正面朝上，这样你就得出错误的结论：正面朝上的概率是1--------过拟合！如果你在模型里加正面朝上概率是0.5的先验，结果就不会那么离谱。这其实就是正则。
2. 最小二乘回归问题：加2范数正则等价于加了高斯分布的先验，加1范数正则相当于加拉普拉斯分布先验。
----------------------
ling wei
求解释这两个“等价”
拿Lasso（1范数正则）举例
其实就是如下概率模型的最大后验。
如果不对w加拉普拉斯分布的先验，最大后验得到的是
其实正则项就是对w的先验分布
