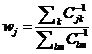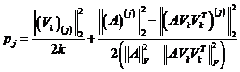机器学习-特征选择 Feature Selection 研究报告
原文:http://www.cnblogs.com/xbinworld/archive/2012/11/27/2791504.html
机器学习-特征选择 Feature Selection 研究报告
注: 这个报告是我在10年7月的时候写的(博士一年级),最近整理电脑的时候翻到,当时初学一些KDD上的paper的时候总结的,现在拿出来分享一下。
毕竟是初学的时候写的,有些东西的看法也在变化,看的人可以随便翻翻,有错指正我。
重点部分:是第3章和第4章对应的两篇paper,具体可以在参考文献里找到,当时还算比较新。
如引用务必请注明本文出自:http://www.cnblogs.com/xbinworld
1 介绍
在计算机视觉、模式识别、数据挖掘很多应用问题中,我们经常会遇到很高维度的数据,高维度的数据会造成很多问题,例如导致算法运行性能以及准确性的降低。特征选取(Feature Selection)技术的目标是找到原始数据维度中的一个有用的子集,再运用一些有效的算法,实现数据的聚类、分类以及检索等任务。
特征选取的目标是选择那些在某一特定评价标准下的最重要的特征子集。这个问题本质上是一个综合的优化问题,具有较高的计算代价。传统的特征选取方法往往是独立计算每一个特征的某一得分,然后根据得分的高低选取前k个特征。这种得分一般用来评价某一特征区分不同聚类的能力。这样的方法在二分问题中一般有不错的结果,但是在多类问题中很有可能会失败。
基于是否知道数据的lebal信息,特征提取方法可以分为有监督和无监督的方法。有监督的的特征提取方法往往通过特征与label之间的相关性来评估特征的重要性。但是label的代价是高昂的,很难在大数据集上进行计算。因此无监督的特征提取方法就显得尤为重要。无监督的方法只利用数据本身所有的信息,而无法利用数据label的信息,因此要得到更好的结果往往更困难。
特征选取是一个热门的研究领域,近年来很多相关工作[2][3][4]被提出,使得特征选取越来越多的受到关注;另外一些关于数据谱分析以及L1正则化模型的研究,也启发了特征选取问题一些新的工作的开展。并且,随着计算机与网络的发展,人们越来越多的关注大规模数据的处理问题,使得研究与应用能够真正衔接在一起。因此无监督的特征选取方法的研究显得更加重要。在本报告中,我们重点关注无监督的特征提取方法。
2 特征选取相关工作
特征选取方法也可以分为包装(Wrapper)类方法与过滤(Filter)类方法。包装类型的方法,经常使用到的算法是聚类。有很多算法同时考虑数据的特征提取以及聚类,为了找到一些特征能够更好的提高数据聚类的性能。然而包装类型的算法往往具有较高的计算代价,因此很难被运用到大规模的数据挖掘分析工作中。
过滤类型的方法相对来说比较常见,也很容易得到扩展。最大方差(Maximum Variance)的方法也许是其中最简单,但也十分有效的算法。该方法本质上是将数据投影到最大方差的方向上。PCA[6]也使用相同的思想,但是它使用转换了的特征,而不是原始数据特征的一个子集。
虽然最大方差的标准可以有效的找到特征来表示数据,但是却不能很好地区分数据。Laplacian Score算法可以有效的提取出那些体现数据潜在流形结构的特征;Fisher Score算法可以有效的区分数据,它给最有效区分数据点(不同类数据点尽可能的分开,而同一类的数据点尽可能的聚在一起)的特征赋予最高的分值。
2.1 降维方法
特征选取算法和降维算法有着非常密切的联系,很多算法的设计都来源于一些经典的降维算法,下面简单介绍几种常见的降维算法(特征选取本质上也是一种降维)。
Principal Component Analysis[6](PCA)是最常用的线性降维方法,它的目标是通过某种线性投影,将高维的数据映射到低维的空间中表示,并期望在所投影的维度上数据的方差最大,以此使用较少的数据维度,同时保留住较多的原数据点的特性。具体实现步骤如下:
X是![]() 矩阵,P表示维度,N表示数据个数。Y是
矩阵,P表示维度,N表示数据个数。Y是![]() 矩阵,d表示降维后的维度,N表示数据个数。
矩阵,d表示降维后的维度,N表示数据个数。
步骤1:先对数据进行中心化预处理,
步骤2:取协方差矩阵最大的d个特征值对应的特征向量作为投影方向W
步骤3:降维后 ,数据由P维降低到d维
将PCA的通过Kernel的方法,也可以运用在非线性降维中,即KPCA[10]。
Laplacian Eigenmaps[8]的直观思想是希望相互间有关系的点(如在一个图中相连的点)在降维后的空间中尽可能的靠近。Laplacian Eigenmaps可以反映出数据内在的流形结构。算法具体实现步骤:
步骤1:构建图
使用某一种方法来将所有的点构建成一个图,例如使用KNN算法,将每个点最近的K个点连上边。K是一个预先设定的值。
步骤2:确定权重
确定点与点之间的权重大小,例如选用热核函数来确定,如果点i和点j相连,那么它们关系的权重设定为:
另外一种可选的简化设定是如果点i,j相连,权重为1,否则权重为0。
步骤3:特征映射
计算拉普拉斯矩阵L的特征向量与特征值:
使用最小的m个非零特征值对应的特征向量作为降维后的结果输出。
Locally linear embedding[7](LLE)是一种非线性降维算法,它能够使降维后的数据较好地保持原有流形结构。
使用LLE将三维数据映射到二维之后,映射后的数据仍能保持原有的数据流形,说明LLE有效地保持了数据原有的流行结构。
但是LLE在有些情况下也并不适用,如果数据分布在整个封闭的球面上,LLE则不能将它映射到二维空间,且不能保持原有的数据流形。那么我们在处理数据中,首先假设数据不是分布在闭合的球面或者椭球面上。
LLE算法认为每一个数据点都可以由其近邻点的线性加权组合构造得到。算法的主要步骤分为三步:(1)寻找每个样本点的k个近邻点;(2)由每个样本点的近邻点计算出该样本点的局部重建权值矩阵;(3)由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值。具体的算法流程如下:
步骤1:
算法的第一步是计算出每个样本点的k个近邻点。例如采用KNN的策略,把相对于所求样本点距离(常用欧氏距离)最近的k个样本点规定为所求样本点的 个近邻点,k是一个预先给定值。
步骤2:
计算出样本点的局部重建权值矩阵W,首先定义重构误差:
以及局部协方差矩阵C:
于是,目标函数最小化:
步骤3:
将所有的样本点映射到低维空间中。映射条件满足如下所示:
要使损失函数值达到最小, 则取Y为M的最小m个非零特征值所对应的特征向量。在处理过程中,将M的特征值从小到大排列,第一个特征值几乎接近于零,那么舍去第一个特征值。通常取第2到m+1间的特征值所对应的特征向量作为输出结果。
本文接下来重点介绍无监督多聚类特征选取[5](第3章)和无监督特征选取PCA[1](第4章)两个新提出的特征选取算法。
3 无监督多聚类特征选取
特征选取的一般问题是不考虑数据本身的结构的,而事实上很多数据本身具有多聚类结构特征,一个好的特征选取方法应该考虑到下面两点:
l 所选取的特征应该可以最好地保持数据的聚类结构特征。最近一些研究表明一些人为产生的数据存在着内在的数据流行结构,这个因素应该被考虑在聚类算法中。
l 所选取的特征应该可以覆盖数据中所有可能的聚类。因为不同的特征维度在区分不同的聚类时具有不同的效果,所以如果选取的特征仅仅可以区分某一些聚类而不能区分所有的聚类是不合适的。
3.1 谱嵌入聚类分析
在第2章中讨论过Laplacian Eigenmaps,假设![]() ,
,![]() 是公式(2)的特征向量。Y的每一行是一个数据点的降维表示。其中K是数据的内在维度,每一个
是公式(2)的特征向量。Y的每一行是一个数据点的降维表示。其中K是数据的内在维度,每一个![]() 体现数据在该维度(可以理解成一个主题,或者是一个概念)上的数据分布。当使用聚类分析时,每一个
体现数据在该维度(可以理解成一个主题,或者是一个概念)上的数据分布。当使用聚类分析时,每一个![]() 可以体现数据在这一个聚类上的分布。因此K往往可以设定成数据聚类的个数。
可以体现数据在这一个聚类上的分布。因此K往往可以设定成数据聚类的个数。
3.2 学习稀疏系数
在得到Y之后,我们可以衡量每一个内在维度的重要性,也就是Y的每一列,同时可以衡量每一个特征区分数据聚类的能力。
给定一个![]() ,通过最小化拟合错误,可以找到一个相关的特征子集,如下:
,通过最小化拟合错误,可以找到一个相关的特征子集,如下:
其中![]() 是一个M维度的向量(X是N*M维矩阵),
是一个M维度的向量(X是N*M维矩阵),![]() 表示L1-norm。
表示L1-norm。![]() 包含了用来近似
包含了用来近似![]() 时每一个特征的系数。由于L1-norm的性质,当
时每一个特征的系数。由于L1-norm的性质,当![]() 足够大时,
足够大时,![]() 的某些系数将会变为0。因此,我们可以选取一些最相关的特征子集。公式(9)本质上是一个回归问题,称作LASSO。
的某些系数将会变为0。因此,我们可以选取一些最相关的特征子集。公式(9)本质上是一个回归问题,称作LASSO。
3.3 特征选取
我们需要从M个特征的数据中选取d个特征。对于一个含有K个聚类的数据来说,我们可以用上面提到的方法来计算出K个系数的系数向量![]() ,每一个
,每一个![]() 的非零元素个数为d(对应d个特征)。显然,如果把所有选取的特征都用上,很有可能会大于d个特征。于是,使用下面这种简单的策略来选取出d个特征。
的非零元素个数为d(对应d个特征)。显然,如果把所有选取的特征都用上,很有可能会大于d个特征。于是,使用下面这种简单的策略来选取出d个特征。
定义每一个特征的MCFS score,如下
将所有的特征根据他们MCFS score降序排列,选取前d个特征。
3.3 计算复杂度分析
算法的计算复杂度从下面几点分析:
l P-近邻图需要![]() 步来构建,同时需要
步来构建,同时需要![]() 步来找到找到每一个点的p个近邻
步来找到找到每一个点的p个近邻
l 在构建好p-近邻图的基础上,需要计算公式(2)的前k个特征向量,利用Lanczos algorithm需要![]() 时间
时间
l 使用LARs来解公式(9),限制是![]() ,需要时间
,需要时间![]() ,因此我们需要
,因此我们需要![]() 的时间来计算K聚类的问题
的时间来计算K聚类的问题
4 无监督特征选取PCA
PCA是一种重要的线性降维算法,广泛运用在社会、经济、生物等各种数据上。在第2章中简单讨论过PCA,这里我们从另外一种角度来描述PCA。
4.1 子空间选取
给定一个数据矩阵![]() ,m为数据个数,n为数据维度。令
,m为数据个数,n为数据维度。令![]() 是数据降维后的维度(特征数),并假设A的列经过中心化。于是,PCA返回的是矩阵A的前k个left singular vectors(一个
是数据降维后的维度(特征数),并假设A的列经过中心化。于是,PCA返回的是矩阵A的前k个left singular vectors(一个![]() 的矩阵
的矩阵![]() )并且将数据投影到
)并且将数据投影到![]() 列向量所在的子空间中。
列向量所在的子空间中。
令![]() 为子空间的投影矩阵,于是最佳投影实际上是在所有可能的K维子空间中,最小化:
为子空间的投影矩阵,于是最佳投影实际上是在所有可能的K维子空间中,最小化:
我们希望找到一种高效的(关于m和n多项式时间内)无监督的特征选取算法,能够挑选出k个特征,使得PCA只作用在这k个特征上的结果和作用全部特征上的结果很接近。为了定义这个接近程度,令C是一个![]() 矩阵,只包含有从A中选取出来的特征。通过计算下面的差,来衡量特征选取的好坏:
矩阵,只包含有从A中选取出来的特征。通过计算下面的差,来衡量特征选取的好坏:
这里![]() 代表投影矩阵(投影到
代表投影矩阵(投影到![]() 的列空间张成的K维空间中),
的列空间张成的K维空间中),![]() 表示矩阵
表示矩阵![]() 的伪逆。这等价于Column Subset Selection Problem(CSSP)问题。
的伪逆。这等价于Column Subset Selection Problem(CSSP)问题。
在现代统计数据分析中,从高维数据中选取出原始的特征(feature selection)比选取出经过操作后的特征(feature extraction)在很多等方面都更有优势。
4.1 两阶段CSSP
在这一节中,介绍一种两阶段的CSSP。具体步骤如下:
算法1:
1. 起始设置
l 计算A的前k个right singular vectors,表示成![]()
2. 随机阶段
3. 确定阶段
具体来看,算法1先要计算A每一列的概率,![]() ,概率分布依赖于A的前k个right singular vectors
,概率分布依赖于A的前k个right singular vectors ![]() ,写成:
,写成:
由上式可以知道,只要得到![]() 就可以算出
就可以算出![]() ,而本算法的时间复杂度主要取决于计算所有的
,而本算法的时间复杂度主要取决于计算所有的![]() 所花费的时间。
所花费的时间。
在随机阶段,算法1随机地选择![]() 中的
中的![]() 列,作为下一阶段的输入。对于
列,作为下一阶段的输入。对于![]() ,,第j列的概率为
,,第j列的概率为![]() 。如果第j列被选择,则放缩因子等于
。如果第j列被选择,则放缩因子等于![]() 。因此在这个阶段的末尾,我们将得到
。因此在这个阶段的末尾,我们将得到![]() 中的
中的![]() 列,以及它们相应的放缩因子。因为随机采样,
列,以及它们相应的放缩因子。因为随机采样,![]() 一般会不等于c;然而很大概率下,
一般会不等于c;然而很大概率下,![]() 不会比c大很多。为了当便表示选出的列和放缩因子,我们使用下面的形式:
不会比c大很多。为了当便表示选出的列和放缩因子,我们使用下面的形式:
首先定义一个![]() 的采样矩阵
的采样矩阵![]() ,
,![]() 初始值为空值,当第j列被选中时就将
初始值为空值,当第j列被选中时就将![]() 加到
加到![]() 中。然后定义
中。然后定义![]() 对角放缩矩阵
对角放缩矩阵![]() ,当第j列被选取时,
,当第j列被选取时,![]() 的第j个对角元素是
的第j个对角元素是![]() 。因此,随机阶段的输出结果就是
。因此,随机阶段的输出结果就是![]() 。
。
在确定阶段,从上一个阶段挑选出来的列中选取k列,实际上就是定义了一个采样矩阵![]() ,在这个阶段之后,就得到了
,在这个阶段之后,就得到了![]() 矩阵
矩阵![]() 作为最后的结果。
作为最后的结果。
6 参考文献
[1] Boutsidis, C., Mahoney, M. W., Drineas, P. Unsupervised feature selection for principal components analysis. In Proceeding of the 14th ACMSIGKDDinternational conference on Knowledge discovery and data mining, 2008, 61-69.
[2] Yu, L., Ding, C., Loscalzo, S. Stable feature selection via dense feature groups. In Proceeding of the 14th ACM SIGKDDinternational conference on Knowledge discovery and data mining, 2008, 803-811.
[3] Forman, G., Scholz, M., Rajaram, S. Feature shaping for linear SVM classifiers. In Proceedings of the 15th ACM SIGKDDinternational conference on Knowledge discovery and data mining, 2009, 299-308.
[4] Loscalzo, S., Yu, L., Ding, C. Consensus group stable feature selection. In Proceedings of the 15th ACM SIGKDDinternational conference on Knowledge discovery and data mining, 2009, 567-576.
[5] D,Cai, C,Zhang,X,He. Unsupervised Feature Selection for Multi-Cluster Data.To be appeared in SIGKDD2010.
[6] Smith, L. I. A tutorial on principal components analysis. Cornell University, USA. 2002, 51,52.
[7] Roweis, S. T., Saul, L. K. Nonlinear dimensionality reduction by locally linear embedding. Science. 2000, 290(5500):2323.
[8] Belkin, M., Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. Advances in neural information processing systems. 2002, 1585-592.
[9] Tenenbaum, J. B., Silva, V., Langford, J. C. A global geometric framework for nonlinear dimensionality reduction. Science. 2000, 290(5500):2319.
[10] Scholkopf, B., Smola, A. J., Muller, K. R. Kernel principal component analysis. Lecture notes in computer science. 1997, 1327583-588.