统计学习三：1.k近邻法

全文引用自《统计学习方法》（李航）

K近邻算法(k-nearest neighbor, KNN) 是一种非常简单直观的基本分类和回归方法，于1968年由Cover和Hart提出。在本文中，主要介绍了分类方法。其输入为特征空间中的点，输出为给定实例的类别，可以选择多个类输出。K近邻算法通过给定的训练集对特征空间进行分类，分类时，对于输入的实例，通过判断其最近的k个实例的类别，选择多数类别为本实例的最终分类。因此，k近邻算法本质上并不具有显示的学习过程。
本篇文章通过介绍K近邻算法的k值选择、距离度量和分类决策规则三要素，来介绍K近邻算法。

1.K近邻算法

K近邻算法最直观的描述就是：给定一个训练集，在新的实例需要分类时，选择训练集中与新的实例点最近的k个点，看这k个点中哪一类的点最多，那么这个新的实例就被分为这一类。
算法形式为：

• 输入：训练数据集

\[T=\{(x_1,y_1),(x_2,y_2),...,(x_{_N},y_{_N})\} \]

其中\(x_i\in X\subseteq R^n\)为实例的特征向量,\(y_i\in Y=\{c_1,c_2,\cdots,c_{_K}\}\)为实例的类别,\(i=1,2,...,N\)；

• 输出：实例\(\overrightarrow{x}\)所属的类y。

1. 根据给定的距离度量，在训练集T中找到与\(\overrightarrow{x}\)最近的k个点，这k个点的邻域记作\(N_k(x)\),

2. 在\(N_k(x)\)中根据分类决策规则(如多数表决)决定\(\overrightarrow{x}\)的类别y：

\[y=\arg\max_{c_j}\sum_{x_i\in N_k(x)}{I(y_i = c_i)},i=1,2,\cdots.N;j=1,2,\cdots,K \]

式中，I为指示函数，当\(y_i=c_i\)时，I为1，否则I为0。

2.K近邻模型

K近邻算法的基本原理，其实是利用训练数据集，对特征空间进行直接的划分。模型的三要素分别是距离度量、k值得选择和分类决策规则

2.1距离度量

K近邻算法进行分类时的主要工作是寻找到距离新的实例点最近的k个训练集中的实例点。因此，最重要的前提条件是确定在特征空间中，计算两个点间距离的方法。K近邻模型的特征空间通常是n维实数向量空间\(R^n\)，通常采用欧式距离作为距离判定标准。通常我们以\(L_p\)距离(\(L_p\)distaince)作为更一般的描述。
假定特征空间X是n维实数向量空间\(R^n,x_i,x_j\in X,x_i=(x_i^{(1)},x_i^{(2)},\cdots,x_i^{(n)})^T,x_j=(x_j^{(1)},x_j^{(2)},\cdots,x_j^{(n)})^T,x_i,x_j\)的\(L_p\)距离定义为：

\[L_p(x_i,x_j) = \left(\sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}|^p\right)^{\frac{1}{p}} \]

式中\(p\geq1\)。
而当\(p=2\)时，称为欧式距离(Euclidean distance)：

\[L_2(x_i,x_j) = \sqrt{\sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}|^2} \]

当\(p=1\)时，称为曼哈顿距离(Manhattan distance):

\[L_1(x_i,x_j) = \sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}| \]

当\(p=\infty\)时，其值为各个坐标距离的最大值：

\[L_{\infty}(x_i,x_j) = \max_l|x_i^{(l)}-x_j^{(l)}| \]

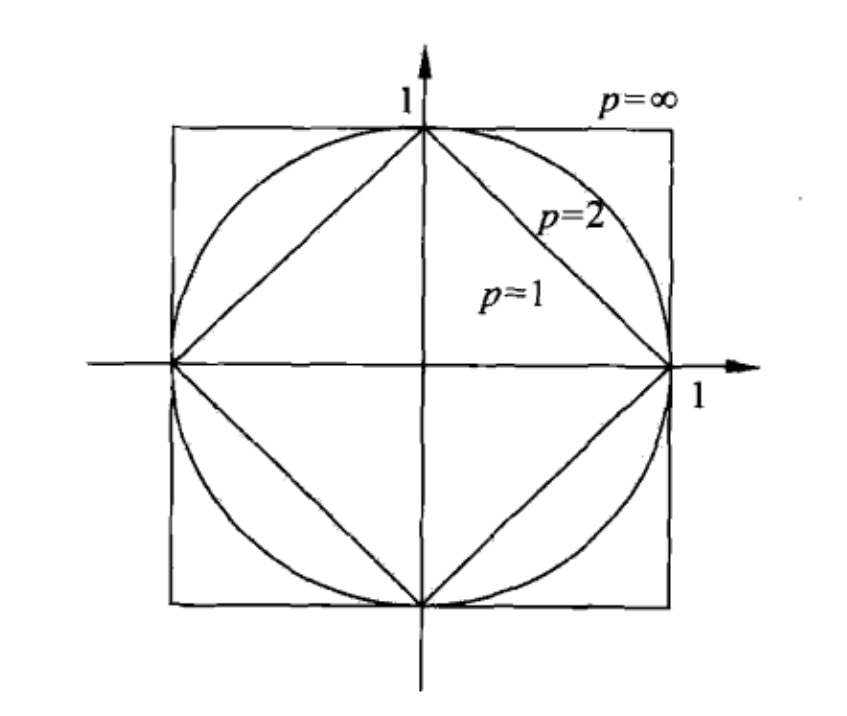
上图为二维空间中p的取值不同时，与原点的\(L_p\)距离为1的点的图形。由此可知，在p不同时，即选择不同的距离度量时，新的实例点所能取到的最近邻点可能是不同的。

2.2K值的选择

k值表示在新的实例点输入时，选择多少个邻近的点做分类，因此其对最终分类的结果影响较大。
若选择较小的k值，则学习的近似误差(approximation error)更小，只有与输入较近，即更为相似的训练点才会对预测结果有影响。但当新的实例点的邻域内有噪声点时，其对分类的结果影响更大，即学习的估计误差(estimation error)更大，预测结果对于邻近的实例点非常敏感，这就意味着模型更容易发生过拟合。
若选择较大的k值，即选择更多的训练点进行类型的判断，可以减少模型的估计误差，但其近似误差会更大。由于新的实例点的邻域内训练点的增多，很多与实例无关的点也可能对分类结果产生影响，使预测结果发生偏离。k值越大，就意味着模型越简单。
若\(k=N\),则不论输入哪个实例，都会选择训练集中数量最多的种类作为最终分类结果。这个模型过于简单，忽略了训练实例中大量的不同类型之间所反映出来的差距和有用信息，因此模型并没有实际的意义。
在实际的应用中，通常会选择较小的k值，并通过交叉验证，来选择最优的k值。

2.3分类决策规则

k近邻算法中，通常采用多数表决规则(majority voting rule)来决定输入实例的类，即在新的实例点的最近的k个训练实例中，哪一类最多，那新的实例点就属于哪一类。
多数表决规则为何有作用，具体有如下解释：
若分类的损失函数为0-1损失函数，那么分类函数为

\[f:R^n \rightarrow \{c_1,c_2,\cdots,c_k\} \]

那么，被误分类的概率为

\[P(Y \neq f(X)) = 1 - P(Y = f(X)) \]

对于给定的实例\(x\in X\),其最近的k个训练实例点构成的集合\(N_k(x)\),若涵盖\(N_k(x)\)的区域的类别是\(c_j\)，那么误分类的概率为：

\[\frac{1}{k} \sum_{x_i \in N_k(x)} I(y_i \neq c_j) = 1 - \frac{1}{k} \sum_{x_i \in N_k(x)} I(y_i = c_j) \]

即，若要使误分类的概率最小，也就是模型的经验风险最小，那么就要使\(\sum_{x_i \in N_k(x)} I(y_i = c_j)\)的值最大。因此，多数表决规则就等价于经验风险最小化。

3.K近邻算法的实现：kd树

由上文中的描述可知，k近邻算法较为简便的实现方式，就是每次计算新的输入实例与所有训练点间的距离，然后从小到大排序，选择距离最小的k个点。这种方式在特征空间维度较大，或训练点较多时，会有极大的效率问题，计算会非常耗时。因此，选择一种能够提高k近邻搜索的速度的方法就成为必要。现在常用的方法是kd树(kd tree) 方法。

3.1 kd树的构造

kd树 是一种对k维特征空间中的实例点进行存储，并能够对其进行高效的检索的数据结构。kd树一般是二叉树，表示对k维空间的一个划分。构造一棵kd树，相当于在不同的维度中，不断用垂直于坐标轴的超平面将对应维度的平面进行分割，构成一系列的k维超矩形区域。kd树的每一个节点就对应了一个超矩形区域。
构造kd树的具体方法是：
输入：k维空间数据集\(T=\{x_1,x_2,\cdots,x_N\}\)，
其中\(x_i = (x_i^{(1)}, x_i^{(2)}, \cdots, x_i^{(n)})^T,i = 1,2,\cdots,N;\)
输出：kd树

1. 选择\(x^{(1)}\)为第一个坐标轴，选择T中所有的实例中\(x^{(1)}\)值的中位数作为切分点，此点作为根节点的值，其余点的\(x^{(1)}\)的值比切分点小的作为左子树，比切分点大的作为右子树，生成深度为1的kd树。

2. 重复以下过程：对于深度为j的节点，选择\(x^{(l)}\)为将要切分的坐标轴，其中\(l = j(\mod k) + 1\)，选择该节点的区域中的所有实例的\(x^{(l)}\)值的中位数为切分点，将中位数对应的实例点作为该节点的值，区域内其他的节点按照\(x^{(l)}\)值的大小分为左右两个部分，小的为左半部区域，大的为右半部区域，从而生成深度为\(j+1\)的子树。

3. 直到被切分的两个子区域都没有实例点时，kd树生成结束，完成了对特征空间的完全划分。

3.2 kd树的搜索

kd树建立完成后，需要对kd树有一种高效且有效的搜索方法。我们不能对树中的每一个节点都去计算与新的实例点间的距离，这样kd树的建立便没有意义。下面以搜索最近邻点为例，介绍一种可以节省对kd树中大部分数据点的搜索的方法，可以大量减少计算量。
输入：已经构造完成的kd树，新的实例点x；
输出：x的最近邻点

1. 在kd树中，找出包含节点x的叶子节点，即从根节点出发，向下访问kd树。若目标点x在当前维度中的坐标值小于节点坐标，则移动到左节点，否则移动到右节点。重复以上过程直到叶子节点为止。

2. 以此叶子节点为当前最近邻点。

3. 以此节点开始向上退回，并在每个节点上进行如下操作：a) 如果该节点保存的实例点比当前的最近邻点距离目标点更近，那么以当前实例点为最近邻点；b) 当前的最近点一定存在于当前点对应的某一个子节点对应的区域中，因此，查找当前节点的另一个子节点对应的区域是否有更近的点。具体做法是，检查另一个子节点对应的区域是否与以目标点为球心、以目标点与当前最近点之间的距离为半径的超球体相交，即判断在当前维度下的另一个子节点与x之间的距离是否比当前最近点与x之间的距离小。若是相交，则可能在另一个子节点对应的区域内存在距目标点更近的点，则移动到另一个子节点上，继续进行最近邻搜索。若不相交，则向上退回。

4. 当退回到根节点，搜索结束，此时记录的最近邻点即为x的最近邻点。

若训练集中的实例点是随机分布的，那么kd树的平均复杂度为\(O(\log N)\)，N是训练集中实例点的数量。kd树对于实例点的数量远大于空间维度的k近邻搜索模型优化程度更高。当空间的维度接近训练实例数时，它的效率就会显著下降，接近线性扫描。