聊聊卷积神经网络CNN
卷积神经网络(Convolutional Neural Network,CNN)是一种被广泛应用于图像识别、语音识别和自然语言处理等领域的深度学习模型。与RNN、Transformer模型组成AI的三大基石。
在卷积神经网络中,相比较普通的神经网络,增加了卷积层(Convolution)和池化层(Pooling)。其结构一般将会是如下:
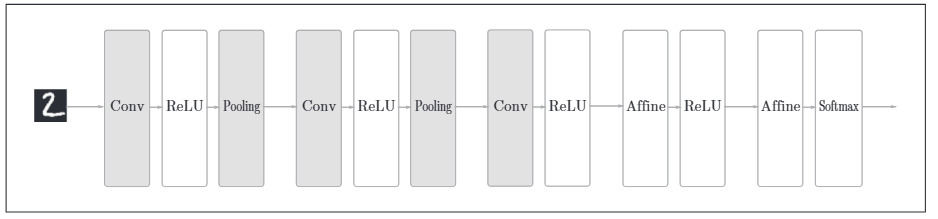
CNN的层连接顺序是"Convolution - ReLU - (Pooling)"(Pooling层有时候可以省略)。
图中的Affine层,也被称为全连接层(Dense层)或仿射层,作用是将输入数据(input)与权重矩阵(W)相乘,然后添加偏置(B),从而进行线性变换。这个线性变换是神经网络中的一个基本操作,用来实现特征映射和模型参数的学习。在几何学领域,Affine层进行的矩阵乘积运算被称为“仿射变换”。仿射变换包括一次线性变换和一次平移,分别对应神经网络的加权和运算与加偏置运算。
卷积层
传统的全连接神经网络(Full-Connected)中忽略了数据的形状,比如,输入数据是图像时,图像通常是高、长、通道三个方向上的3维形状。但是向全连接层(FC)输入时,需要将3维数据拉平为1维数据。全连接层会忽视形状,将全部的输入数据作为相同的神经元(同一纬度的神经元)处理,所以无法利用与形状相关的信息。
卷积层可以保持形状不变。当输入数据是图像时,卷积层会以3维数据的形式接受输入数据,并以3维数据的形式输出至下一层。因此,CNN架构的网络可以正确理解图像等具有形状的数据。
卷积层进行的处理就是卷积运算。卷积运算相当于图像处理中的"滤波器运算"。而这个"滤波器"也就是卷积层的卷积核。正是通过它在输入数据上的滑动来提取特征。其运算过程如下所示:
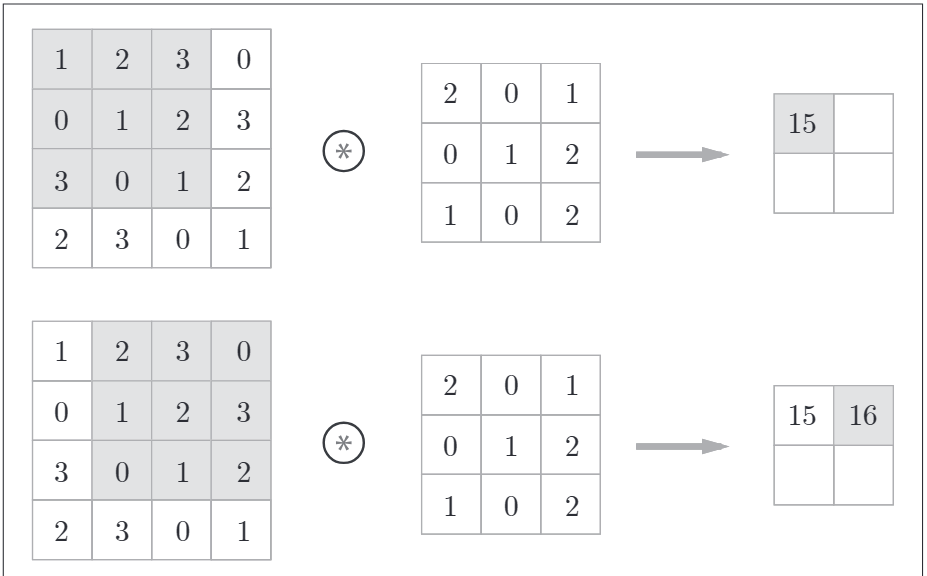
将各个位置上滤波器的元素与输入的对应元素相乘,然后再求和。最后将结果保存到输出的对应位置。将这个过程在所有的位置运算一遍,就可以得到卷积运算的输出。
注意,这里的计算是把输入的行 乘 卷积核的行; 然后再依次累加,得到最终值。
卷积操作可以分为以下几个步骤:
-
将卷积核与输入数据的一个小区域进行逐元素相乘。
-
将相乘得到的结果求和,得到卷积操作的输出值。
-
将卷积核在输入数据上滑动一个固定的步长,重复上述操作,直到覆盖整个输入数据。
通过卷积操作,卷积核可以提取输入数据中的局部特征。这是因为卷积核的每个权重都对应着输入数据中的一个局部区域,通过逐元素相乘和求和的操作,卷积核可以将这个局部区域的特征信息进行提取。
卷积核具有以下几个重要的特点:
-
特征提取:卷积核通过滑动窗口的方式在输入数据上进行卷积操作,从而提取输入数据中的局部特征。这些特征可以用于后续的分类、检测和识别等任务。
-
参数共享:卷积核的权重是共享的,即在卷积操作中使用的同一个卷积核对输入数据的不同区域进行卷积操作时,使用的是相同的权重。这种参数共享的方式大大减少了模型的参数量,提高了模型的训练效率。
-
空间不变性:卷积操作具有平移不变性,即对于输入数据中的特征在空间上的平移,卷积操作的输出结果不会发生变化。这种空间不变性使得卷积神经网络能够更好地处理图像等具有平移不变性的数据。
填充
在卷积层处理之前,支持对输入数据做填充,即在输入数据的周围填入固定的数据(比如0,1等)。而输入数据的形状改变就会影响到输出数据的大小,这也是使用填充的作用,通过填充输入数据的周围数据,保持输出数据的大小,因此将数据传入到下一层时就不会出现丢失或数据不全。
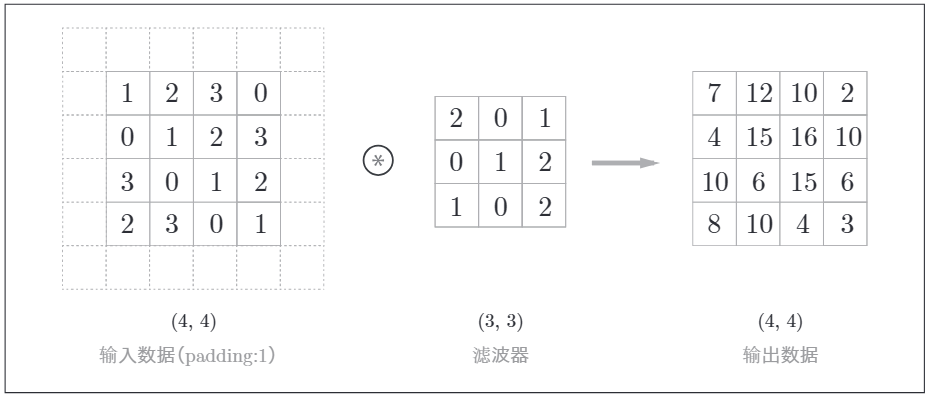
向输入数据的周围填入0,图中用虚线表示填充,并省略了填充内容"0".
步幅
应用卷积核的位置间隔即为步幅。默认一般都是1,也可以调整为2或是其它的。步幅可以减少输出的高、宽。
输出数据的计算
有个公式可以算出经过卷积核运算后的输出数据高与宽, 假设输入大小为(H,W),卷积核大小为(FH,FW),输出大小为(OH,OW),填充为P,步幅为S:
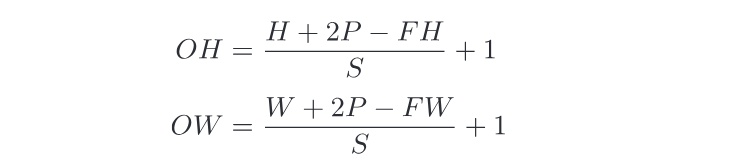
三维卷积
图像是3维数据,除了高、长方向还有通道方向。增加了通道,会按通道进行输入数据与滤波器的卷积运算。
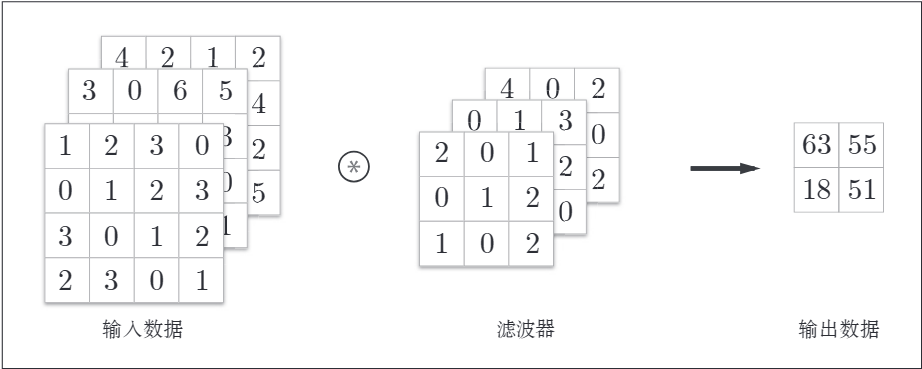
需要注意的是,三维卷积的运算中,输入数据和卷积核的通道数要设置为相同的值。
三维数据的书写格式为(channel, height, width),卷积核的书写格式也是如此,其运算可简化如下:
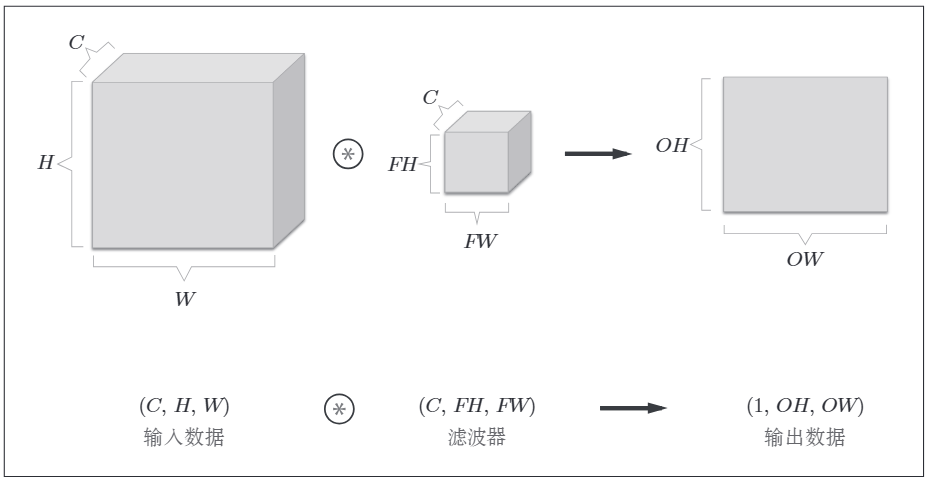
输出是1个通道的特征,如果需要多通道,可以叠加起来,其表现形式如下:
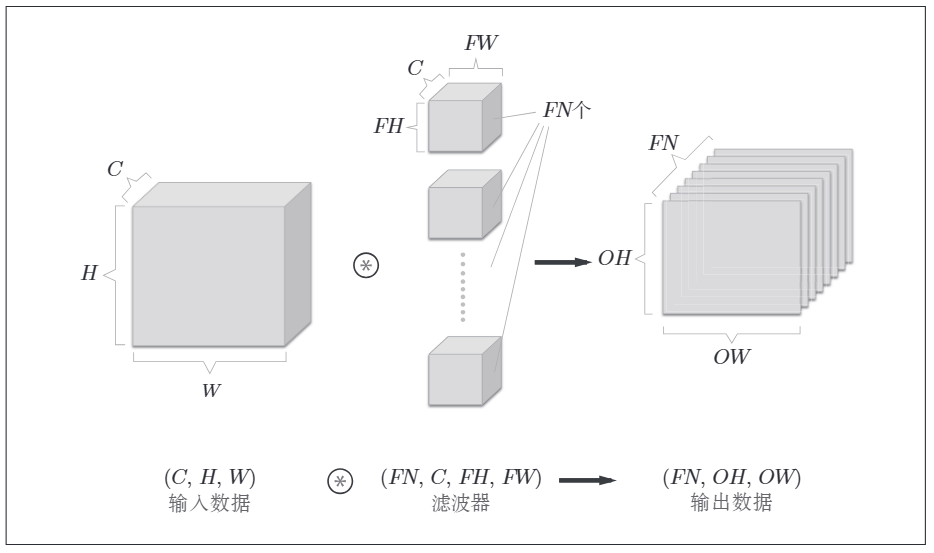
应该应用N个卷积核,输出特征数也生成了N个。
多维的数据在不同的框架(pytorch、TensorFlow)中其表现形式也是不一样的,一般都是按照张量的阶度来标识数据维度。CNN的四维数据,其格式可以表示为(batch_num,channel, height, width)
其它
在某些CNN框架中,会应用小卷积核运算,比如1×1卷积,3×3卷积;还有一种分组卷积;一个卷积层中多尺寸的卷积核等等。这些算是卷积神经网络中的深入知识点,也可以了解下。
池化层
池化是缩小高、长方向上的空间的运算;对输入的特征图进行降采样,减少特征图的维度,同时保留重要的特征信息。
池化层的计算有两种: 最大池化(Max Pooling)和平均池化(Average Pooling)。最大池化选择窗口内的最大值作为输出,而平均池化则计算窗口内值的平均值。这两种方式都能有效地减少特征图的尺寸,进而降低计算复杂度。
如下,按步幅为2,进行2*2窗口的Max池化,在上一层的输出数据上应用窗口,滑动,每次取窗口内的最大值。
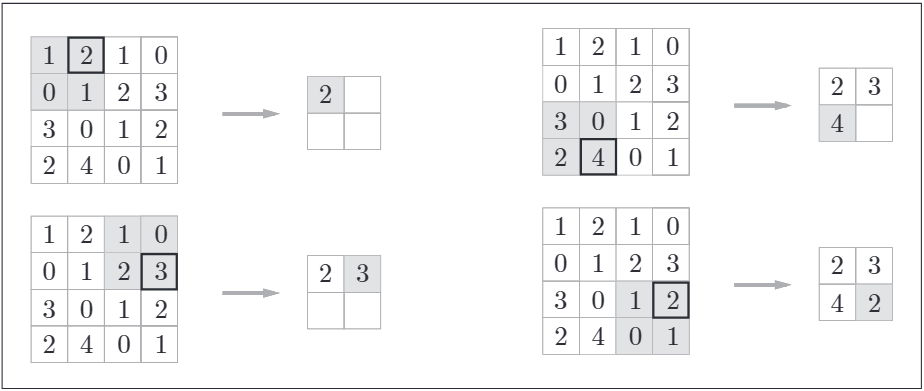
这篇博文写得不错,可以更深入的了解池化层:




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 清华大学推出第四讲使用 DeepSeek + DeepResearch 让科研像聊天一样简单!
· 推荐几款开源且免费的 .NET MAUI 组件库
· 实操Deepseek接入个人知识库
· 易语言 —— 开山篇
· 【全网最全教程】使用最强DeepSeekR1+联网的火山引擎,没有生成长度限制,DeepSeek本体