如何使用 pytorch 实现 SSD 目标检测算法

前言

SSD 的全称是 Single Shot MultiBox Detector，它和 YOLO 一样，是 One-Stage 目标检测算法中的一种。由于是单阶段的算法，不需要产生所谓的候选区域，所以 SSD 可以达到很高的帧率，同时 SSD 中使用了多尺度的特征图来预测目标，所以 mAP 可以比肩甚至超过 Faster R-CNN。在这篇博客中，我们会详细地介绍 SSD 的原理，并使用 pytorch 来实现 SSD。

模型结构

VGG16

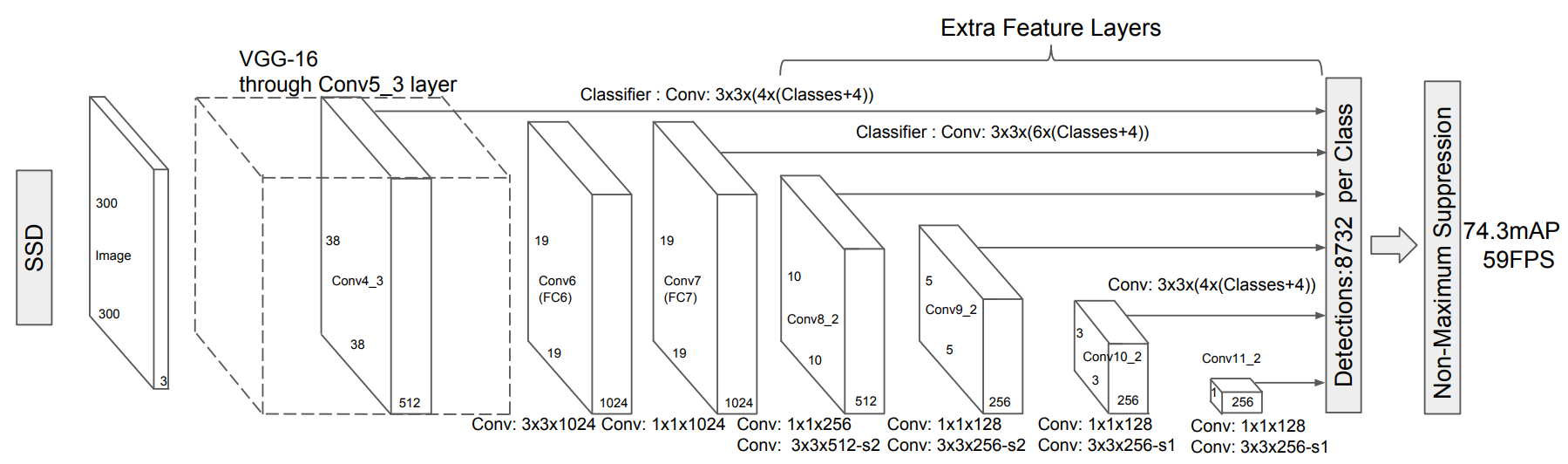
SSD 的结构如上图所示，可以看到 SSD 使用 VGG16 为主干网络，但是在 VGG16 的结构上做了如下修改：

1. 去掉了全连接层 FC6 和 FC7，替换成了卷积层 Conv6 和 Conv7
2. 将 Conv6 前面的最大值池化层从 MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False) 换成 MaxPool2d(kernel_size=3, stride=1, padding=1, dilation=1, ceil_mode=False)，这样就可以保证输入 Conv6 的特征图大小不变
3. Conv6 使用 3×3 大小、膨胀率为 6 的膨胀卷积来增大感受野
4. Conv7 使用 1×1 大小的普通卷积

总结下来 SSD 中的 VGG16 实现代码为：

def vgg16(batch_norm=False) -> nn.ModuleList:
    """ 创建 vgg16 模型

    Parameters
    ----------
    batch_norm: bool
        是否在卷积层后面添加批归一化层
    """
    layers = []
    in_channels = 3
    cfg = [64, 64, 'M', 128, 128, 'M', 256, 256,
           256, 'C', 512, 512, 512, 'M', 512, 512, 512]

    for v in cfg:
        if v == 'M':
            layers.append(nn.MaxPool2d(2, 2))
        elif v == 'C':
            layers.append(nn.MaxPool2d(2, 2, ceil_mode=True))
        else:
            conv = nn.Conv2d(in_channels, v, 3, padding=1)

            # 如果需要批归一化的操作就添加一个批归一化层
            if batch_norm:
                layers.extend([conv, nn.BatchNorm2d(v), nn.ReLU(True)])
            else:
                layers.extend([conv, nn.ReLU(True)])

            in_channels = v

    # 将原始的 fc6、fc7 全连接层替换为卷积层
    layers.extend([
        nn.MaxPool2d(3, 1, 1),
        nn.Conv2d(512, 1024, 3, padding=6, dilation=6),  # conv6 使用空洞卷积增加感受野
        nn.ReLU(True),
        nn.Conv2d(1024, 1024, 1),                        # conv7
        nn.ReLU(True)
    ])

    layers = nn.ModuleList(layers)
    return layers

下面这张图直观地显示了原本的 VGG16 (torchvision.models 的实现) 和 SSD 中 VGG16 的区别，可以看到从 (30): MaxPool2d 开始二者就变得不一样了：

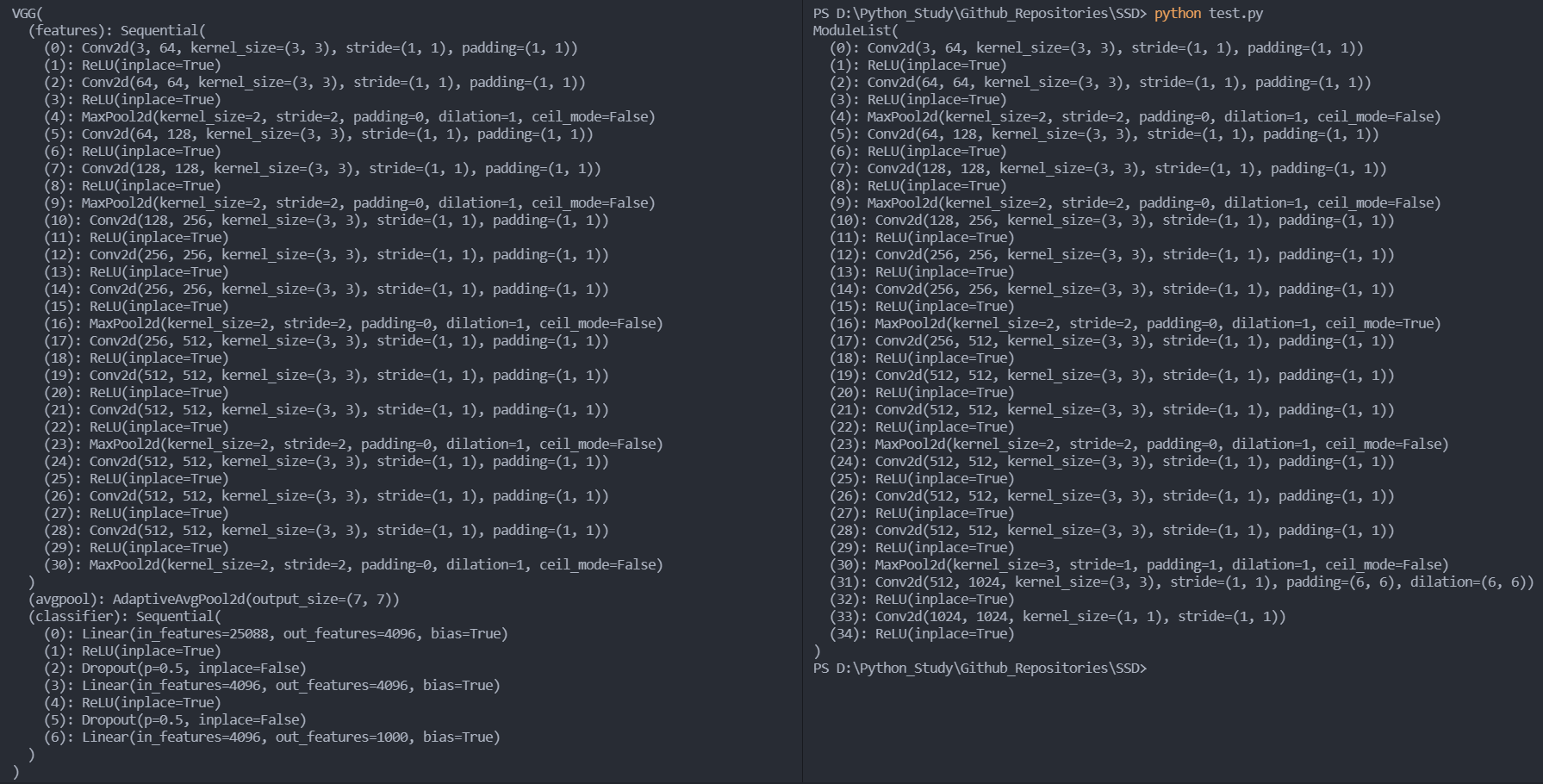
Extra Feature Layers

为了更好地检测大目标物体，SSD 在 VGG16 后面多添加了几个卷积块 Conv8_2、Conv9_2、Conv10_2 和 Conv11_2，他们的具体结构为：

self.extras = nn.ModuleList([
    nn.Conv2d(1024, 256, 1),                        # conv8_2
    nn.Conv2d(256, 512, 3, stride=2, padding=1),
    nn.Conv2d(512, 128, 1),                         # conv9_2
    nn.Conv2d(128, 256, 3, stride=2, padding=1),
    nn.Conv2d(256, 128, 1),                         # conv10_2
    nn.Conv2d(128, 256, 3),
    nn.Conv2d(256, 128, 1),                         # conv11_2
    nn.Conv2d(128, 256, 3),
])

先验框

前面提及了 SSD 使用多尺度的特征图来检测目标，所谓的多尺度，其实就是用了不同大小的特征图。假设我们向 SSD 神经网络输入了一张 300×300×3 的图像，经过一些列的卷积和池化之后，会得到下面 6 个要用来检测目标的特征图：

• Conv4_3 输出的 39×39×512 的特征图

• Conv7 输出的 19×19×1024 的特征图

• Conv8_2 输出的 10×10×512 的特征图

• Conv9_2 输出的 5×5×256 的特征图

• Conv10_2 输出的 3×3×256 的特征图

• Conv11_2 输出的 1×1×256 的特征图

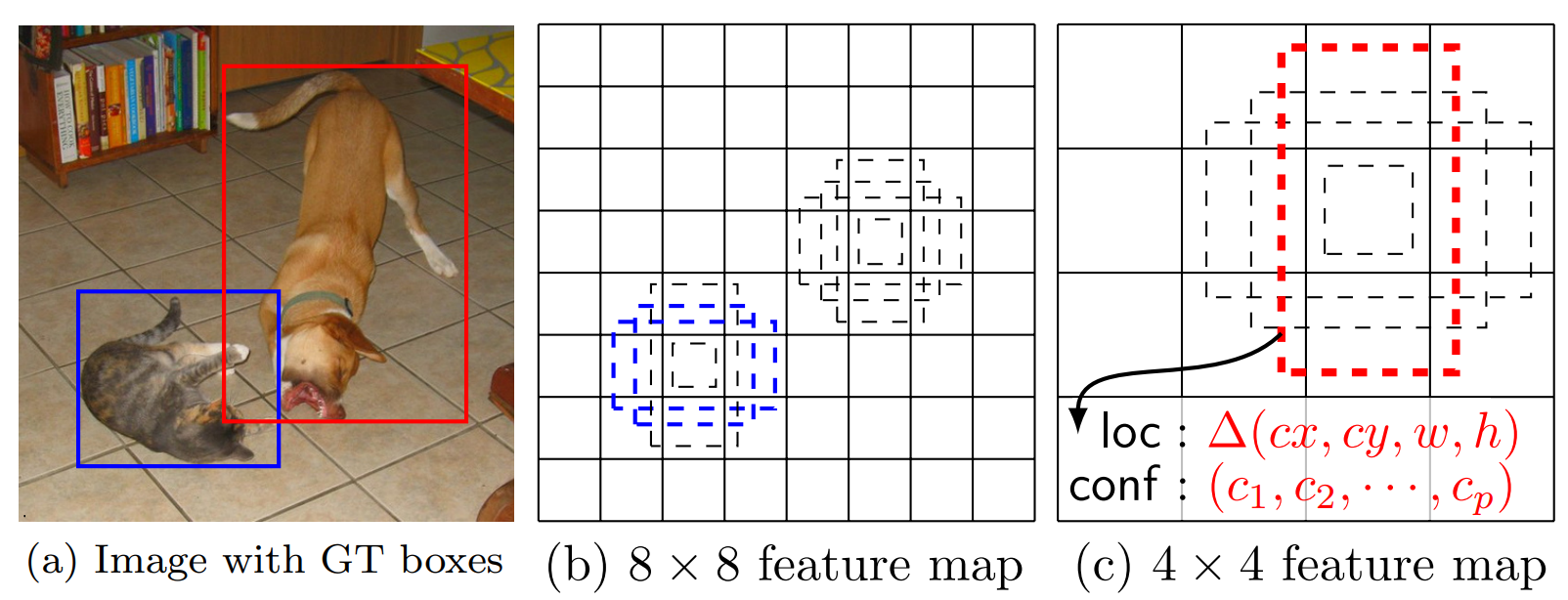
随着网络的加深，特征图会越来越小，小目标的特征可能会丢失掉，所以我们用大的特征图用来检测小目标，小的特征图用来检测大目标。如下图的子图 (a) 所示，用蓝色方框标出的猫猫比较小，所以应该由较大的 8×8 特征图（这里的 8 × 8 只是为了和 4×4 形成大小对比，实际中用的不是 8×8）检测出来，而红色方框标出的狗狗较大，就应该使用 4×4 大小的特征图来检测。但是具体要怎么用这些特征图来进行目标检测呢？这就引出了先验框（default box）的概念。如子图 (b) 所示，我们会在每张特征图的每个像素点处产生一些具有不同长宽比 \(a_r\) 和尺度 \(scale\) 的方框，称之为先验框。只要知道了输入图像的大小（此处为 300×300）、 \(a_r\) 和 \(scale\) ，我们就能确定出这些先验框的大小。

\(scale\) 的计算方式

如果我们给前面列出的 6 个特征图从 0 到 5 编个号，第 \(k\) 个特征图中最小的那个正方形先验的 \(scale\) 记为 \(s_k\) ，定义 \(s_k\) 的计算公式为：

\[s_k = s_{min} + \frac{s_{max} - s_{min}}{m-1} (k-1), \quad k \in [1, m] \]

其中 \(s_{max}\) 为 0.9，\(s_{min}\) 为 0.2。从上述公式可以看出，\(s_k\) 与 \(k\) 成正相关，也就是说：特征图越小，\(s_k\) 反而越大，因为小特征图要用来检测大目标。在论文中，作者直接将 \(s_0\) 设置为 \(s_{min}/2\) 即 0.1，剩下的 5 个特征图的 \(s_k\) 由上述公式给出，此时 \(m=5\)，\(s_1=0.2\)，\(s_2=0.375\)，\(s_3=0.55\)，\(s_4=0.725\)，\(s_5=0.9\)。将 \(s_k\) 乘以输入图像的尺寸 300 可以得到先验框的真实大小，计算得到的结果是 \([30,\ 60,\ 112.5,\ 165,\ 217.5,\ 270]\)，这就产生了一个问题：我图像都是整数大小的，你先验框怎么能带小数呢？所以又将上述计算 \(s_k\) 的公式魔改为：

\[s_k=\left(\lfloor s_{min}\times100 \rfloor + \lfloor \frac{\lfloor s_{max}\times100 \rfloor - \lfloor s_{min}\times 100 \rfloor}{m-1}\rfloor (k-1)\right)/100, \quad k \in [1, m] \]

重新计算可得 \(s_1=0.2\)，\(s_2=0.37\)，\(s_3=0.54\)，\(s_4=0.71\)，\(s_5=0.88\)，对应先验框的大小为 \([30,\ 60,\ 111,\ 162,\ 213,\ 264]\)，如此一来我们便得到了每个特征图中最小的正方形先验框的大小。从上图可以看到除了这个小正方形以外，还会有一个大正方形，那么这个大正方形的尺寸又该如何确定呢？论文中使用几何平均公式来确定：\(s_k'=\sqrt{s_ks_{k+1}}\)，对于最小的特征图，\(s_{k+1}\) 取 1.05。小声比比：\(s_k\) 的定义公式就没什么意思，我直接给出几个能算出整数值预测框大小的 \(s_k\) 不就完事了吗，似乎没必要搞得这么麻烦 _(:3」∠)_。

\(a_r\) 计算公式

论文中给出的 \(a_r\) 为 \(\left\{1,\ 1',\ 2,\ \frac{1}{2},\ 3,\ \frac{1}{3} \right\}\), 前面两个长宽比对应了小正方形 \(s_k\) 和大正方形 \(s_k'\)，后面 4 个长宽比对应了剩余 4 个长方形先验框，这 4 个长方形先验框的宽度和高度由该式子给出：\(w_k^a=s_k\sqrt{a_r},\ h_k^a=s_k/\sqrt{a_r}\) 。实际上并不是每个特征图中都设置 \(a_r\) 为 \(\left\{1,\ 1',\ 2,\ \frac{1}{2},\ 3,\ \frac{1}{3} \right\}\)，第一个和最后两个特征图只使用 \(\left\{1,\ 1',\ 2,\ \frac{1}{2} \right\}\) 来生成先验框。这里先验框的宽度和高度都是小数，因为实际使用中我们会将 ground truth 边界框的坐标 \((x_{min},\ y_{min},\ x_{max},\ y_{max})\) 即左上角和右下角坐标归一化。

生成先验框

我们会使用每个像素点 \((i,\ j)\) 的中心坐标 \((c_x,\ c_y)\) 来生成先验框 \((c_x,\ c_y,\ w_k^a,\ h_k^a)\)，其中 \(c_x=\frac{i+0.5}{|f_k|}\)，\(c_y=\frac{j+0.5}{|f_k|}\)，这里的 \(|f_k|\) 是特征图的尺寸，除以它就可以将中心坐标归一化。注意：图像以左上角为原点，向右为 \(x\) 轴正方向，向下为 \(y\) 轴正方向。图像对应到矩阵中就是以列索引 \(j\) 为 \(x\) 坐标值，行索引 \(i\) 为 \(y\) 坐标值，所以代码中的 \(c_x=\frac{j+0.5}{|f_k|}\)，\(c_y=\frac{i+0.5}{|f_k|}\)。

# coding:utf-8
from itertools import product
from math import sqrt

import torch


class PriorBox:
    """ 用来生成先验框的类 """

    def __init__(self, image_size=300, feature_maps: list = None, min_sizes: list = None,
                 max_sizes: list = None, aspect_ratios: list = None, steps: list = None, **kwargs):
        """
        Parameters
        ----------
        image_size: int
            图像大小

        feature_maps: list
            特征图大小

        min_sizes: list
            特征图中的最小正方形先验框的尺寸

        max_sizes: list
            下一个特征图中的最小正方形先验框的尺寸

        aspect_ratios: list
            长宽比

        steps: list
            步长，可理解为感受野大小
        """
        self.image_size = image_size
        self.feature_maps = feature_maps or [38, 19, 10, 5, 3, 1]
        self.min_sizes = min_sizes or [30, 60, 111, 162, 213, 264]
        self.max_sizes = max_sizes or [60, 111, 162, 213, 264, 315]
        self.steps = steps or [8, 16, 32, 64, 100, 300]
        self.aspect_ratios = aspect_ratios or [
            [2], [2, 3], [2, 3], [2, 3], [2], [2]]

    def __call__(self):
        """ 得到所有先验框

        Returns
        -------
        boxes: Tensor of shape `(n_priors, 4)`
            先验框
        """
        boxes = []

        for k, f in enumerate(self.feature_maps):
            f_k = self.image_size / self.steps[k]

            for i, j in product(range(f), repeat=2):
                # 中心坐标，向右为 x 轴正方向，向下为 y 轴正方向
                cx = (j+0.5) / f_k
                cy = (i+0.5) / f_k

                # 1 和 1'
                s_k = self.min_sizes[k]/self.image_size
                s_k_prime = sqrt(s_k*self.max_sizes[k]/self.image_size)

                boxes.append([cx, cy, s_k, s_k])
                boxes.append([cx, cy, s_k_prime, s_k_prime])

                # 根据其余的 ar 计算宽和高
                for ar in self.aspect_ratios[k]:
                    boxes.append([cx, cy, s_k*sqrt(ar), s_k/sqrt(ar)])
                    boxes.append([cx, cy, s_k/sqrt(ar), s_k*sqrt(ar)])

        boxes = torch.Tensor(boxes).clamp(min=0, max=1)
        return boxes

现在我们来计算一下每个特征图生成的先验框的个数：

• 第 1 个特征图：\(38\times38\times4=5776\)
• 第 2 个特征图：\(19 \times 19 \times 6 = 2166\)
• 第 3 个特征图：\(10 \times 10 \times 6 = 600\)
• 第 4 个特征图：\(5\times 5\times 6=150\)
• 第 5 个特征图：\(3\times 3\times 4=36\)
• 第 6 个特征图：\(1\times 1\times 4=4\)

所以在一张 300×300 的图上总共生成了 \(5776+2166+600+150+36+4=8732\) 个先验框。

位置偏移量和置信度

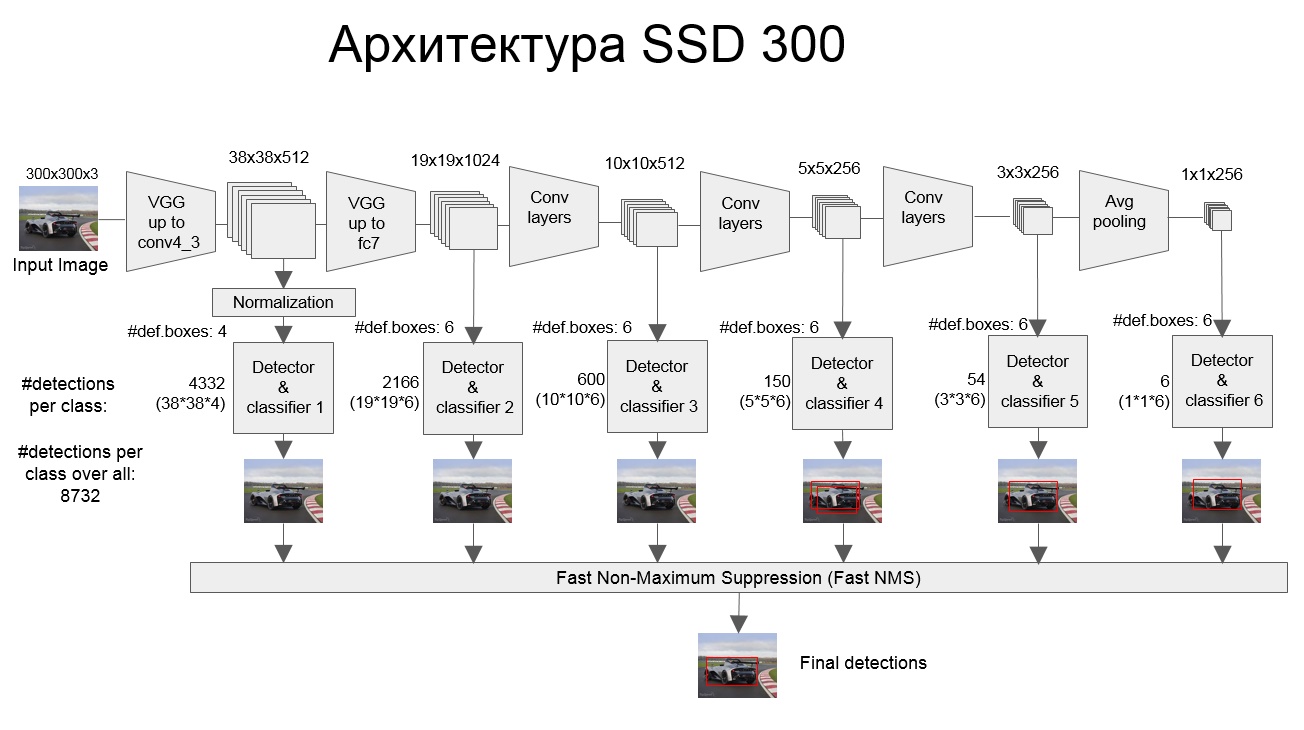
现在我们只拿到了一堆密密麻麻的先验框，还不知道先验框中有没有物体，如果有的话是什么物体？同时由于先验框的位置是固定的，如果直接拿它来定位目标，肯定会非常不准，所以我们还需要预测先验框和真实框（ground truth box，已归一化）之间的偏移量。我们对每个特征图使用了上图中的 Detector & Classifier 模块，里面是卷积层，用来预测先验框和真实框之间的偏移量，以及先验框之中是否有某类物体的置信度（0~1 之间）。

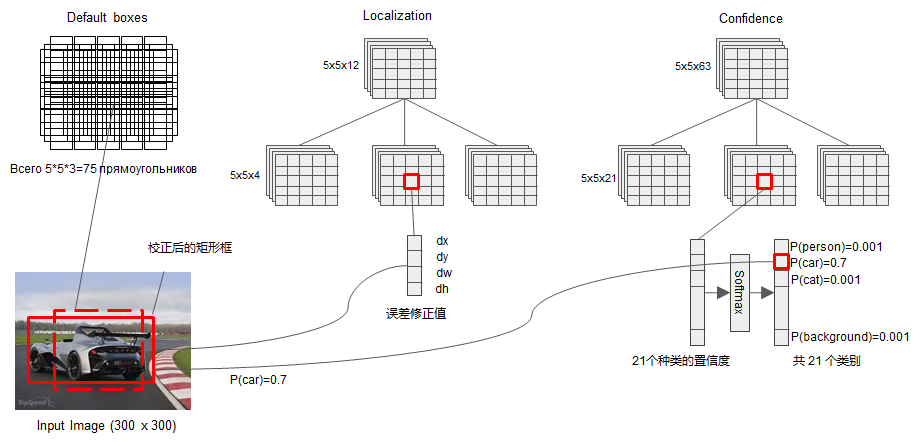
假设我们要检测 n_classes 类物体（包括背景），特征图的通道数为 in_channels，每个像素点位置生成的先验框的个数为 k。由于每个先验框都要预测 n_classes 个类的置信度，所以 classifier 的输出通道数为 k*n_classes ，同理偏移位置应该包含 4 个坐标值，所以 Detector 的输出通道数为 k*4。写成代码就是如下形式：

self.confs = nn.ModuleList([
    nn.Conv2d(512, n_classes*4, 3, padding=1),
    nn.Conv2d(1024, n_classes*6, 3, padding=1),
    nn.Conv2d(512, n_classes*6, 3, padding=1),
    nn.Conv2d(256, n_classes*6, 3, padding=1),
    nn.Conv2d(256, n_classes*4, 3, padding=1),
    nn.Conv2d(256, n_classes*4, 3, padding=1),
])
self.locs = nn.ModuleList([
    nn.Conv2d(512, 4*4, 3, padding=1),
    nn.Conv2d(1024, 4*6, 3, padding=1),
    nn.Conv2d(512, 4*6, 3, padding=1),
    nn.Conv2d(256, 4*6, 3, padding=1),
    nn.Conv2d(256, 4*4, 3, padding=1),
    nn.Conv2d(256, 4*4, 3, padding=1),
])

第一个特征图在检测之前还有一个 L2 Normalization 的操作，根据论文中的说法：

Since, as pointed out in [12], conv4_3 has a different feature scale compared to the other layers, we use the L2 normalization technique introduced in [12] to scale the feature norm at each location in the feature map to 20 and learn the scale during back propagation.

由于 Conv4_3 输出的特征图较大，在没有使用 Batch Normalization 的情况下应该加一个 L2 Normalization 的操作来消除尺度差异性，但是作者没有使用传统的标准化操作，他还在每个通道维度乘上一个可学习的缩放量 \(scale\)，并将初始值设置为 20，关于更多标准化的介绍可以参见博客 《为什么要做特征归一化/标准化？》 。上述标准化操作对应的代码为：

class L2Norm(nn.Module):
    """ L2 标准化 """

    def __init__(self, n_channels: int, scale=20):
        """
        Parameters
        ----------
        n_channels: int
            通道数

        scale: float
            l2标准化的缩放比
        """
        super().__init__()
        self.gamma = scale
        self.eps = 1e-10
        self.n_channels = n_channels
        self.weight = nn.Parameter(Tensor(self.n_channels))
        self.reset_parameters()

    def reset_parameters(self):
        init.constant_(self.weight, self.gamma)

    def forward(self, x: Tensor):
        norm = x.pow(2).sum(dim=1, keepdim=True).sqrt()+self.eps
        x = torch.div(x, norm)
        # 将 weight 的维度变为 [1, n_channels, 1, 1]
        y = x*self.weight[None, ..., None, None]
        return y

截止目前，我们已经可以让神经网络来预测先验框的偏移量和类别置信度了，下面是 SSD 神经网络的前馈过程：

class SSD(nn.Module):
    """ SSD 神经网络模型 """

    def __init__(self, n_classes: int, variance=(0.1, 0.2), top_k=200, conf_thresh=0.01,
                 nms_thresh=0.45, image_size=300, **config):
        """
        Parameters
        ----------
        n_classes: int
            要预测的种类数，包括背景

        variance: Tuple[float, float]
            先验框的方差

        top_k: int
            每个类的边界框上限

        conf_thresh: float
            置信度阈值

        nms_thresh: float
            nms 中 IOU 阈值

        image_size: int
            图像尺寸

        **config:
            关于先验框生成的配置
        """
        super().__init__()

        if len(variance) != 2:
            raise ValueError("variance 只能有 2 元素")

        self.n_classes = n_classes
        self.image_size = image_size
        config['image_size'] = image_size

        # 生成先验框
        self.priorbox_generator = PriorBox(**config)
        self.prior = Tensor(self.priorbox_generator())

        # 各个模块
        self.vgg = vgg16()
        self.l2norm = L2Norm(512, 20)
        self.extras = nn.ModuleList([
            # 同上，省略不写
        ])
        self.confs = nn.ModuleList([
            # 同上，省略不写
        ])
        self.locs = nn.ModuleList([
            # 同上，省略不写
        ])

        # 很快介绍
        self.detector = Detector(
            n_classes, variance, top_k, conf_thresh, nms_thresh)

    def forward(self, x: Tensor):
        """
        Parameters
        ----------
        x: Tensor of shape `(N, 3, H, W)`
            图像数据

        Returns
        -------
        loc: Tensor of shape `(N, n_priors, 4)`
            偏移量

        conf: Tensor of shape `(N, n_priors, n_classes)`
            类别置信度

        prior: Tensor of shape `(n_priors, 4)`
            先验框
        """
        loc = []
        conf = []
        sources = []

        # 批大小
        N = x.size(0)

        # 计算从 conv4_3 输出的特征图
        for layer in self.vgg[:23]:
            x = layer(x)

        # 保存 conv4_3 输出的 l2 标准化结果
        sources.append(self.l2norm(x))

        # 计算 vgg16 后面几个卷积层的特征图
        for layer in self.vgg[23:]:
            x = layer(x)

        # 保存 conv7 的输出的特征图
        sources.append(x)

        # 计算后面几个卷积层输出的特征图
        for i, layer in enumerate(self.extras):
            x = F.relu(layer(x), inplace=True)
            if i % 2 == 1:
                sources.append(x)

        # 使用分类器和探测器进行预测并将通道变为最后一个维度方便堆叠
        for x, conf_layer, loc_layer in zip(sources, self.confs, self.locs):
            loc.append(loc_layer(x).permute(0, 2, 3, 1).contiguous())
            conf.append(conf_layer(x).permute(0, 2, 3, 1).contiguous())

        # 输出维度为 (batch_size, n_priors, n_classes) 和 (batch_size, n_priors, 4)
        conf = torch.cat([i.view(N, -1) for i in conf], dim=1)
        loc = torch.cat([i.view(N, -1) for i in loc], dim=1)

        return loc.view(N, -1, 4), conf.view(N, -1, self.n_classes),  self.prior

    @torch.no_grad()
    def predict(self, x: Tensor):
        """
        Parameters
        ----------
        x: Tensor of shape `(N, 3, H, W)`
            图像数据

        Returns
        -------
        out: Tensor of shape `(N, n_classes, top_k, 5)`
            检测结果，最后一个维度的前四个元素为边界框的坐标 `(xmin, ymin, xmax, ymax)`，最后一个元素为置信度
        """
        loc, conf, prior = self(x)
        return self.detector(loc, F.softmax(conf, dim=-1), prior.to(loc.device))

编码和解码

之前刻意没有提及偏移量的使用方式，现在来展开讲讲。假设第 \(i\) 个先验框的位置为 \(d_i=(d_i^{cx},\ d_i^{cy},\ d_i^w,\ d_i^h)\)，第 \(j\) 个真实框的位置为 \(g_j=(g_j^{cx},\ g_j^{cy},\ g_j^w,\ g_j^h)\)，那么偏差量真值应该为：

\[\hat{g}_j^{cx}=(g_j^{cx}-\ d_i^{cx})/d_i^w\\ \hat{g}_j^{cy}=(g_j^{cy}-\ d_i^{cy})/d_i^h\\ \hat{g}_j^{w}=\log(\frac{g_j^{w}}{d_i^w})\\ \hat{g}_j^{h}=\log(\frac{g_j^{h}}{d_i^h}) \]

实际上代码中还会使用一个方差 \(varaiances=(center\_variacen,\ size\_variance)\)，且 \(variances=(0.1,\ 0.2)，\)使得上述公式变化为：

\[\hat{g}_j^{cx}=(g_j^{cx}-\ d_i^{cx})/d_i^w/center\_variance\\ \hat{g}_j^{cy}=(g_j^{cy}-\ d_i^{cy})/d_i^h/center\_variance\\ \hat{g}_j^{w}=\log(\frac{g_j^{w}}{d_i^w})/size\_variance\\ \hat{g}_j^{h}=\log(\frac{g_j^{h}}{d_i^h})/size\_variance \]

作者对这个操作的解释是：

It is used to encode the ground truth box w.r.t. the prior box. You can check this function. Note that it is used in the original MultiBox paper by Erhan etal. It is also used in Faster R-CNN as well. I think the major goal of including the variance is to scale the gradient. Of course you can also think of it as approximate a gaussian distribution with variance of 0.1 around the box coordinates.

也就是说这个 \(variances\) 可以用来缩放梯度，加快训练过程。

使用了 \(variances\) 之后，由偏差量预测值 \(l=(l^{cx},\ l^{cy},\ l^w,\ l^h)\) 和先验框解码出边界框预测值的公式为：

\[g^{cx}_{\text{predict}}=d^w*center\_variance*l^{cx}+d^{cx}\\ g^{cy}_{\text{predict}}=d^h*center\_variance*l^{cy}+d^{cy}\\ g^{w}_{\text{predict}}=d^we^{size\_variance*l^w}\\ g^{h}_{\text{predict}}=d^he^{size\_variance*l^h} \]

根据上述公式，编码和解码的代码为：

def encode(prior: Tensor, matched_bbox: Tensor, variance: tuple):
    """ 编码先验框和与边界框之间的偏置量

    Parameters
    ----------
    prior: Tensor of shape `(n_priors, 4)`
        先验框，坐标形式为 `(cx, cy, w, h)`

    matched_bbox: Tensor of shape `(n_priors, 4)`
        匹配到的边界框，坐标形式为 `(xmin, ymin, xmax, ymax)`

    variance: Tuple[float, float]
        先验框方差

    Returns
    -------
    g: Tensor of shape `(n_priors, 4)`
        编码后的偏置量
    """
    matched_bbox = corner_to_center(matched_bbox)
    g_cxcy = (matched_bbox[:, :2]-prior[:, :2]) / (variance[0]*prior[:, 2:])
    g_wh = torch.log(matched_bbox[:, 2:]/prior[:, 2:]+1e-5) / variance[1]
    return torch.cat((g_cxcy, g_wh), dim=1)


def decode(loc: Tensor, prior: Tensor, variance: tuple):
    """ 根据偏移量和先验框位置解码出边界框的位置

    Parameters
    ----------
    loc: Tensor of shape `(n_priors, 4)`
        先验框，坐标形式为 `(cx, cy, w, h)`

    prior: Tensor of shape `(n_priors, 4)`
        先验框，坐标形式为 `(cx, cy, w, h)`

    variance: Tuple[float, float]
        先验框方差

    Returns
    -------
    g: Tensor of shape `(n_priors, 4)`
        边界框的位置
    """
    bbox = torch.cat((
        prior[:, :2] + prior[:, 2:] * variance[0] * loc[:, :2],
        prior[:, 2:] * torch.exp(variance[1] * loc[:, 2:])), dim=1)
    bbox = center_to_corner(bbox)
    return bbox

处理多余的先验框

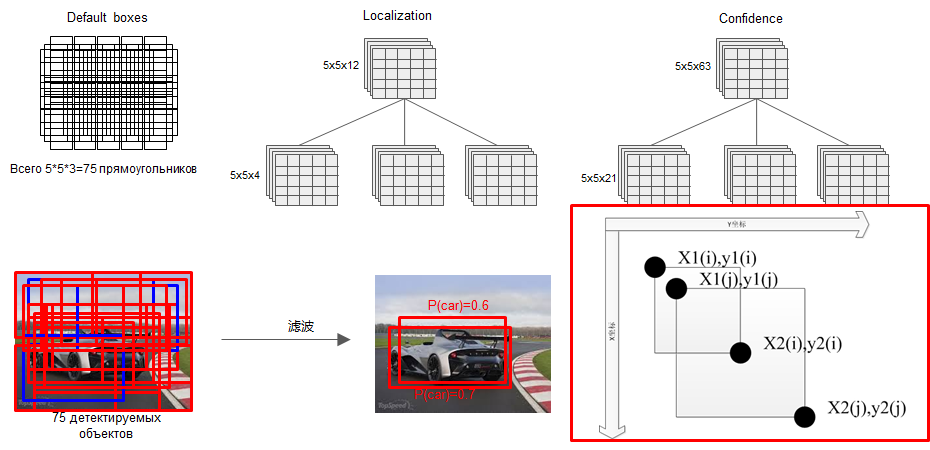
思考一下这个问题：现在我生成了这么多的预测框，相邻的预测框很可能检测出来的是同一个物体，如果将这些预测全部画出来，图片上将会是密密麻麻的一大片。该如何解决这个问题呢？这时候我们就需要使用非极大值抑制（NMS）算法。

交并比

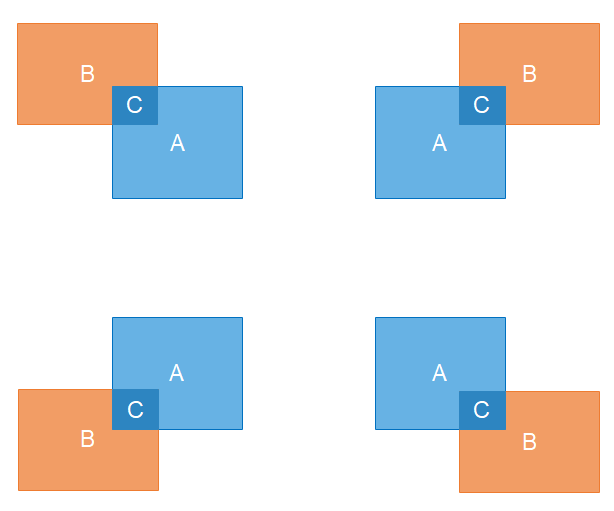
在 NMS 算法中使用到了交并比（Interection-over-unio，简称 IOU）的概念，用来衡量两个预测框之间的重叠程度。假设我们有两个预测框 \(b_0=(x_{min0},\ y_{min0},\ x_{max0},\ y_{max0})\) 和 \(b_1=(x_{min1},\ y_{min1},\ x_{max1},\ y_{max1})\) ，固定 \(b_0\) 的位置不变，移动 \(b_1\)，他们之间会有四种重叠情况，如下图所示，此时交并比计算公式为 \(IOU=C/(A+B-C)\)，就是交集面积除以并集面积。虽然图中有四种重叠情况，但是计算的时候可以合并为一种 \(C=w_c*h_c\)：

• 交集 \(C\) 的宽度 \(w_c=x_2-x_1\)，其中 \(x_2=\min\{x_{max0},\ x_{max1}\}\)，\(x_1=\max\{x_{min0},\ x_{min1} \}\)；
• 交集 \(C\) 的高度 \(h_c=y_2-y_1\)，其中 \(y_2=\min\{y_{max0},\ y_{max1}\}\)，\(y_1=\max\{y_{min0},\ y_{min1} \}\)；

NMS 算法流程

假设我们要检测的类是上图中的跑车，输入 NMS 算法的就是所有的预测框boxes和这些预测框对于包含跑车的置信度 scores。如果是 300×300 的输入图像，那么预测框的维度就应该是 \((8732, 4)\)，每行一个预测框，共 8732 个。下面 NMS 算法的流程：

1. 将 boxes 按照置信度 scores进行降序排序，并且只留下前 top_k 个预测框；
2. 初始化一个空列表 keep 用于保存最终留下的预测框；
3. 从 boxes中选出置信度最高的那个预测框 \(b_0\)，将该预测框添加到 keep 中；
4. 计算该预测框与其余预测框的交并比 iou，如果某个预测框 \(b_i\) 与预测框 \(b_0\) 的交并比大于阈值 overlap_thresh，就将预测框 \(b_i\) 从 boxes 中移除；
5. 重复上述步骤，直到 boxes 为空，返回 keep

上述过程对应的代码为：

def nms(boxes: Tensor, scores: Tensor, overlap_thresh=0.5, top_k=200):
    """ 非极大值抑制，去除多余的预测框

    Parameters
    ----------
    boxes: Tensor of shape `(n_priors, 4)`
        预测框，坐标形式为 `(xmin, ymin, xmax, ymax)`

    scores: Tensor of shape `(n_priors, )`
        某个类的每个先验框的置信度

    overlap_thresh: float
        IOU 阈值，大于阈值的部分预测框会被移除，值越小保留的框越少

    top_k: int
        保留的预测框个数上限

    Returns
    -------
    indexes: LongTensor of shape `(n, )`
        保留的边界框的索引
    """
    keep = []
    if boxes.numel() == 0:
        return torch.LongTensor(keep)

    # 每个预测框的面积
    x1 = boxes[:, 0]
    y1 = boxes[:, 1]
    x2 = boxes[:, 2]
    y2 = boxes[:, 3]
    area = (x2-x1)*(y2-y1)

    # 对分数进行降序排序并截取前 top_k 个索引
    _, indexes = scores.sort(dim=0, descending=True)
    indexes = indexes[:top_k]

    while indexes.numel():
        i = indexes[0]
        keep.append(i)

        # 最后一个索引时直接退出循环
        if indexes.numel() == 1:
            break

        # 其他的预测框和当前预测框的交集
        right = x2[indexes].clamp(max=x2[i].item())
        left = x1[indexes].clamp(min=x1[i].item())
        bottom = y2[indexes].clamp(max=y2[i].item())
        top = y1[indexes].clamp(min=y1[i].item())
        inter = ((right-left)*(bottom-top)).clamp(min=0)

        # 计算 iou
        iou = inter/(area[i]+area[indexes]-inter)

        # 保留 iou 小于阈值的边界框，自己和自己的 iou 为 1
        indexes = indexes[iou < overlap_thresh]

    return torch.LongTensor(keep)

如果对每一个类的预测框都是用 NMS 算法，代码就会如下所示：

# coding:utf-8
import torch
from torch import Tensor

from utils.box_utils import decode, nms


class Detector:
    """ 用于处理 SSD 网络输出的探测器类，在测试时起作用 """

    def __init__(self, n_classes: int, variance: list, top_k=200, conf_thresh=0.01, nms_thresh=0.45) -> None:
        """
        Parameters
        ----------
        n_classes: int
            类别数，包括背景

        variance: Tuple[float, float]
            先验框方差

        top_k: int
            预测框数量的上限

        conf_thresh: float
            置信度阈值

        nms_thresh: float
            nms 操作中 iou 的阈值，越小保留的预测框越少
        """
        self.n_classes = n_classes
        self.conf_thresh = conf_thresh
        self.nms_thresh = nms_thresh
        self.variance = variance
        self.top_k = top_k

    def __call__(self, loc: Tensor, conf: Tensor, prior: Tensor):
        """ 生成预测框

        Parameters
        ----------
        loc: Tensor of shape `(N, n_priors, 4)`
            预测的偏移量

        conf: Tensor of shape `(N, n_priors, n_classes)`
            类别置信度，需要被 softmax 处理过

        prior: Tensor of shape `(n_priors, 4)`
            先验框

        Returns
        -------
        out: Tensor of shape `(N, n_classes, top_k, 5)`
            检测结果，最后一个维度的前四个元素为边界框的坐标 `(xmin, ymin, xmax, ymax)`，最后一个元素为置信度
        """
        N = loc.size(0)

        # 一张图中可能有多个相同类型的物体，所以多一个 n_classes 维度
        out = torch.zeros(N, self.n_classes, self.top_k, 5)

        for i in range(N):
            # 解码出边界框
            bbox = decode(loc[i], prior, self.variance)
            conf_scores = conf[i].clone()   # Shape: (n_priors, n_classes)

            for c in range(1, self.n_classes):
                # 将置信度小于阈值的置信度元素滤掉
                mask = conf_scores[:, c] > self.conf_thresh
                scores = conf_scores[:, c][mask]    # Shape: (n_prior', )

                # 如果所有的先验框都没有预测出这个类，就直接跳过
                if scores.size(0) == 0:
                    continue

                # 将置信度小于阈值的边界框滤掉
                boxes = bbox[mask]

                # 非极大值抑制，将多余的框滤除
                indexes = nms(boxes, scores, self.nms_thresh, self.top_k)
                out[i, c, :len(indexes)] = torch.cat(
                    (boxes[indexes], scores[indexes].unsqueeze(1)), dim=1)

        return out

训练模型

匹配先验框和真实框

在训练之前，我们需要标识出哪些先验框中包含目标，哪些没有包含。包含物体的先验框被称为正样本，没有包含的是负样本（对应的就是背景类）。如果包含目标的话，我们还应该确定先验框包含的是什么类别的目标。为了确定正负样本，需要将先验框和真实框进行匹配。匹配的流程为：

1. 计算所有先验框和一张图片中的所有真实框的交并比，假设先验框的个数为 n_priors，真实框的个数为 n_objects，那么计算得到的交并比矩阵 iou 维度为 (n_priors, n_objects)，iou 的第 \(i\) 行第 \(j\) 列的元素就代表第 \(i\) 和先验框和第 \(j\) 个真实框的交并比；
2. 对于交并比矩阵 iou，我们沿着 dim=0 的方向进行max计算可以得到和每个真实框交并比最大的那个先验框，沿着 dim=1 的方向进行max计算可以得到和每个先验框交并比最大的那个真实框；
3. 将和每个真实框匹配的最好的先验框标记为正样本，其余的都是负样本。但是这样会带来一个问题：先验框很多而正样本很少，也就是说正负样本的数量差距会很大，会给训练带来困难。所以我们还需要进行下一步；
4. 对于那些没有被标记为正样本的先验框，如果和他们匹配的最好的那个真实框的交并比大于阈值 overlap_thresh，我们也将这个先验框标记为正样本。

总结下来就是每个真实框至少匹配一个先验框，而每个先验框不一定都会有一个与之匹配的真实框。匹配过程的代码为：

def match(overlap_thresh: float, prior: Tensor, bbox: Tensor, variance: tuple, label: Tensor):
    """ 匹配先验框和边界框真值

    Parameters
    ----------
    overlap_thresh: float
        IOU 阈值

    prior: Tensor of shape `(n_priors, 4)`
        先验框，坐标形式为 `(cx, cy, w, h)`

    bbox: Tensor of shape `(n_objects, 4)`
        边界框真值，坐标形式为 `(xmin, ymin, xmax, ymax)`

    variance: Tuple[float, float]
        先验框方差

    label: Tensor of shape `(n_objects, )`
        类别标签

    Returns
    -------
    loc: Tensor of shape `(n_priors, 4)`
        编码后的先验框和边界框的位置偏移量

    conf: Tensor of shape `(n_priors, )`
        先验框中的物体所属的类
    """
    # 计算每个先验框和一张图片中的每个真实框的交并比
    iou = jaccard_overlap(center_to_corner(prior), bbox)

    # 获取和每个边界框匹配地最好的先验框的 iou 和索引，返回值形状 (n_objects, )
    best_prior_iou, best_prior_index = iou.max(dim=0)

    # 获取和每个先验框匹配地最好的边界框的 iou 和索引，返回值形状为 (n_priors, )
    best_bbox_iou, best_bbox_index = iou.max(dim=1)

    # 边界框匹配到的先验框不能再和别的边界框匹配，即使 iou 小于阈值也必须匹配，所以填充一个大于1的值
    best_bbox_iou.index_fill_(0, best_prior_index, 2)
    for i in range(len(best_prior_index)):
        best_bbox_index[best_prior_index[i]] = i

    # 挑选出和先验框匹配的边界框，形状为 (n_priors, 4)
    matched_bbox = bbox[best_bbox_index]

    # 标记先验框中的物体所属的类，形状为 (n_priors, )，+1 是为了让出背景类的位置
    conf = label[best_bbox_index]+1
    conf[best_bbox_iou < overlap_thresh] = 0

    # 对先验框的位置进行编码
    loc = encode(prior, matched_bbox, variance)

    return loc, conf


def jaccard_overlap(prior: Tensor, bbox: Tensor):
    """ 计算预测的先验框和边界框真值的交并比，四个坐标为 `(xmin, ymin, xmax, ymax)`

    Parameters
    ----------
    prior: Tensor of shape `(A, 4)`
        先验框

    bbox: Tensor of shape  `(B, 4)`
        边界框真值

    Returns
    -------
    iou: Tensor of shape `(A, B)`
        交并比
    """
    A = prior.size(0)
    B = bbox.size(0)

    # 将先验框和边界框真值的 xmax、ymax 以及 xmin、ymin进行广播使得维度一致，(A, B, 2)
    # 再计算 xmax 和 ymin 较小者、xmin 和 ymin 较大者，W=xmax较小-xmin较大，H=ymax较小-ymin较大
    xy_max = torch.min(prior[:, 2:].unsqueeze(1).expand(A, B, 2),
                       bbox[:, 2:].broadcast_to(A, B, 2))
    xy_min = torch.max(prior[:, :2].unsqueeze(1).expand(A, B, 2),
                       bbox[:, :2].broadcast_to(A, B, 2))

    # 计算交集面积
    inter = (xy_max-xy_min).clamp(min=0)
    inter = inter[:, :, 0]*inter[:, :, 1]

    # 计算每个矩形的面积
    area_prior = ((prior[:, 2]-prior[:, 0]) *
                  (prior[:, 3]-prior[:, 1])).unsqueeze(1).expand(A, B)
    area_bbox = ((bbox[:, 2]-bbox[:, 0]) *
                 (bbox[:, 3]-bbox[:, 1])).broadcast_to(A, B)

    return inter/(area_prior+area_bbox-inter)

经过上述匹配过程之后我们会得到维度为 (n_priors, 4) 的偏移量真实值和 (n_priors, ) 的类别标签。实际的位置损失计算中不会使用到负样本。

损失函数

损失函数由置信度损失和定位损失组成，定义公式为：

\[L(x,c,l,g)=\frac1N\left( L_{conf}(x,c)+\alpha L_{loc}(x,l,g) \right) \]

其中 \(x\in \{0,1 \}\) ，\(c\) 为置信度预测值，\(l\) 为位置偏差量预测值，\(g\) 为位置偏差量真值，\(N\) 为正样本的数量，如果 \(N\) 为 0，则损失也会被置为 0。实际计算中 \(\alpha\) 取值为 1。

位置损失

位置损失的计算公式为：

\[L_{loc}(x,l,g)=\sum_{i\in Pos}^N \sum_{m\in \{ cx,cy,w,h\}}x_{ij}^k\ {\rm smooth_{L1}}\left( l_i^m-\hat{g}_j^m \right) \]

看起来好像很复杂的样子，我们来分解一下。假设某张图片上有 n_objects 个真实框，我们的 SSD 产生了 n_priors 个先验框，匹配出了 n_positives 个正样本。\(x_{ij}^k\) 代表第 \(i\) 个正样本的类是否和第 \(j\) 个真实框的类相同，如果相同则为 1，否则为 0。\(l_i\) 代表了第 \(i\) 个正样本的位置偏差量预测值，\(\hat{g}^m_j\) 代表第 \(i\) 个正样本和第 \(j\) 个真实框的位置偏差量真实值。实际计算中只要将 nms() 输出的 loc_t 和神经网络匹配出来的 loc_pred 根据正样本的索引进行切片再用 \(\rm{smooth_{L_1}}\) 计算一下损失即可。

置信度损失

置信度损失的计算公式如下，实际上就是使用了交叉熵损失：

\[L_{conf}(x, c) = -\sum_{i\in Pos}^{N} x_{ij}^{p} \log (\hat{c}_{i}^{p}) - \sum_{i\in N_{eg}} \log (\hat{c}_{i}^{0}),\quad \text{where}\ \hat{c}_{i}^{p} = \frac {\exp(c_{i}^{p})}{\sum_{ p} \exp(c_{i}^{p})} \]

为了让正负样本数量均衡，论文中使用了困难样本挖掘的方法对负样本进行抽样，使正负样本的数量比为 \(1:3\)，具体计算过程如下：

1. 给定正样本输入为 \(N_p\) 和正负样本比值 \(1:3\)，则可以得到负样本的数量 \(N_{eg}=3N_p\);
2. 计算负样本的置信度损失
3. 根据置信度损失对负样本进行排序，选取损失最高的前 \(N_{eg}\) 个负样本来计算 \(L_{conf}\)

困难样本挖掘的代码如下：

@torch.no_grad()
def hard_negative_mining(conf_pred: Tensor, conf_t: Tensor, neg_pos_ratio: int):
    """ 困难样本挖掘

    Parameters
    ----------
    conf_pred: Tensor of shape `(N, n_priors, n_classes)`
        神经网络预测的类别置信度

    conf_t: Tensor of shape `(N, n_priors)`
        类别标签

    neg_pos_ratio: int
        负样本和正样本个数比
    """
    # 计算负样本损失，shape: (N, n_priors)
    loss = -F.log_softmax(conf_pred, dim=2)[:, :, 0]

    # 计算每一个 batch 的正样本和负样本个数
    pos_mask = conf_t > 0
    n_pos = pos_mask.long().sum(dim=1, keepdim=True)
    n_neg = n_pos*neg_pos_ratio

    # 选取出损失最高的负样本
    loss[pos_mask] = 0
    _, indexes = loss.sort(dim=1, descending=True)
    _, rank = indexes.sort(dim=1)
    neg_mask = rank < n_neg

    return pos_mask | neg_mask

损失函数代码

# coding:utf-8
from typing import Tuple, List

import torch
from torch import nn
from torch import Tensor
from torch.nn import functional as F

from utils.box_utils import match, hard_negative_mining


class SSDLoss(nn.Module):
    """ 损失函数 """

    def __init__(self, n_classes: int, variance=(0.1, 0.2), overlap_thresh=0.5, neg_pos_ratio=3, use_gpu=True, **kwargs):
        """
        Parameters
        ----------
        n_classes: int
            类别数，包括背景

        variance: Tuple[float, float]
            先验框方差

        overlap_thresh: float
            IOU 阈值，默认为 0.5

        neg_pos_ratio: int
            负样本和正样本的比例，默认 3:1

        use_gpu: bool
            是否使用 gpu
        """
        super().__init__()

        if len(variance) != 2:
            raise ValueError("variance 只能有 2 元素")

        self.use_gpu = use_gpu
        self.variance = variance
        self.n_classes = n_classes
        self.neg_pos_ratio = neg_pos_ratio
        self.overlap_thresh = overlap_thresh

    def forward(self, pred: Tuple[Tensor, Tensor, Tensor], target: List[Tensor]):
        """ 计算损失

        Parameters
        ----------
        pred: Tuple[Tensor]
            SSD 网络的预测结果，包含以下数据：
            * loc: Tensor of shape `(N, n_priors, 4)`
            * conf: Tensor of shape `(N, n_priors, n_classes)`
            * prior: Tensor of shape `(n_priors, 4)`

        target: list of shape `(N, )`
            标签列表，每个标签的形状为 `(n_objects, 5)`，包含边界框位置和类别，每张图中可能不止有一个目标
        """
        loc_pred, conf_pred, prior = pred
        N = conf_pred.size(0)
        n_priors = prior.size(0)

        # 将先验框和边界框 ground truth 匹配，loc_t 保存编码后的偏移量
        loc_t = torch.Tensor(N, n_priors, 4)
        conf_t = torch.Tensor(N, n_priors)
        prior = prior.detach()
        for i in range(N):
            bbox = target[i][:, :-1].detach()
            label = target[i][:, -1].detach()
            loc_t[i], conf_t[i] = match(
                self.overlap_thresh, prior, bbox, self.variance, label)

        if self.use_gpu:
            loc_t = loc_t.cuda()
            conf_t = conf_t.cuda()

        # 正样本标记，索引的 shape: (N, n_priors, 4)，会将所有正样本选出来合成为一维向量
        positive = conf_t > 0   # Shape: (N, n_priors)
        pos_mask = positive.unsqueeze(positive.dim()).expand_as(loc_pred)

        # 方框位置损失
        loc_positive = loc_pred[pos_mask].view(-1, 4)
        loc_t = loc_t[pos_mask].view(-1, 4)
        loc_loss = F.smooth_l1_loss(loc_positive, loc_t, reduction='sum')

        # 困难样本挖掘
        mask = hard_negative_mining(conf_pred, conf_t, self.neg_pos_ratio)

        # 置信度损失
        conf_pred = conf_pred[mask].view(-1, self.n_classes)
        conf_t = conf_t[mask].type(torch.int64)
        conf_loss = F.cross_entropy(conf_pred, conf_t, reduction='sum')

        # 将损失除以正样本个数
        n_positive = loc_positive.size(0)
        loc_loss /= n_positive
        conf_loss /= n_positive

        return loc_loss, conf_loss

数据增强

为了让模型更加鲁棒，我们可以对原始数据做一些增强操作，比如调整图像大小、色调、对比度、颜色通道顺序等等，论文中作者还进行了随机裁剪的操作，这种操作有可能返回以下三种图像：

1. 啥都不做，直接返回原始图像
2. 随机裁剪一块区域，并且裁剪出来的区域和原始图像中的边界框的交并比的最小值应该大于某个阈值，文中取 0.1、0.3、0.5、0.7 和 0.9
3. 随机裁剪一块区域，对裁剪出来的区域没有交并比要求

对于随机裁剪的区域，他们的长宽比应该在 0.5~2 之间。由于裁剪过后，裁剪区域包含的边界框可能只占了原始边界框的一小部分，所以论文中只保留了中心点落在裁剪区域的那些边界框（实际上保留的是边界框和裁剪区域的重叠部分）。对于上述的随机裁剪操作实现代码如下：

class Transformer:
    """ 图像增强抽象类 """

    def transform(self, image: ndarray, bbox: ndarray, label: ndarray):
        """ 对输入的图像进行增强

        Parameters
        ----------
        image: `~np.ndarray` of shape `(H, W, 3)`
            图像，图像模式是 RGB 或者 HUV，没有特殊说明默认 RGB 模式

        bbox: `~np.ndarray` of shape `(n_objects, 4)`
            边界框

        label: `~np.ndarray` of shape `(n_objects, )`
            类别标签

        Returns
        -------
        image, bbox, label:
            增强后的数据
        """
        raise NotImplementedError("图像增强方法必须被重写")

class RandomSampleCrop(Transformer):
    """ 随机裁剪 """

    def __init__(self):
        super().__init__()
        self.sample_options = [
            # 直接返回原图
            None,
            # 随机裁剪，裁剪区域和边界框的交并比有阈值要求
            (0.1, None),
            (0.3, None),
            (0.7, None),
            (0.9, None),
            # 随机裁剪
            (None, None),
        ]

    def transform(self, image: ndarray, bbox: ndarray, label: ndarray):
        h, w, _ = image.shape

        while True:
            mode = randchoice(self.sample_options)

            # 直接返回原图
            if mode is None:
                return image, bbox, label

            min_iou, max_iou = mode
            if min_iou is None:
                min_iou = float('-inf')
            if max_iou is None:
                max_iou = float('inf')

            # 最多尝试 50 次，避免死循环
            for _ in range(50):

                # 随机选取采样区域的宽高
                ww = random.uniform(0.3*w, w)
                hh = random.uniform(0.3*h, h)

                # 要求宽高比在 0.5 ~ 2 之间
                if not 0.5 <= hh/ww <= 2:
                    continue

                # patch 的四个坐标
                left = random.uniform(high=w-ww)
                top = random.uniform(high=h-hh)
                rect = np.array([left, top, left+ww, top+hh], dtype=np.int)

                # 交并比不满足阈值条件就舍弃这个 patch
                iou = jaccard_overlap_numpy(rect, bbox)
                if iou.min() > max_iou or iou.max() < min_iou:
                    continue

                # 裁剪下 patch
                patch = image[rect[1]:rect[3], rect[0]:rect[2]]

                # 判断边界框的中心有没有落在 patch 里面
                centers = (bbox[:, :2]+bbox[:, 2:])/2
                m1 = (centers[:, 0] > rect[0]) & (centers[:, 1] > rect[1])
                m2 = (centers[:, 0] < rect[2]) & (centers[:, 1] < rect[3])
                mask = m1 & m2

                # 如果没有任何一个边界框的中心在 patch 里面就舍弃这个 patch
                if not mask.any():
                    continue

                # 中心落在 patch 里面的边界框及其标签
                bbox_ = bbox[mask].copy()
                label_ = label[mask]

                # 对 patch 里面的边界框进行坐标平移，使其以 patch 的左上角为原点
                bbox_[:, :2] = np.clip(bbox_[:, :2]-rect[:2], 0, np.inf)
                bbox_[:, 2:] = np.clip(
                    bbox_[:, 2:]-rect[:2], 0, rect[2:]-rect[:2]-1)

                return patch, bbox_, label_

关于更多图像增强的操作可以参见【SSD算法】史上最全代码解析-数据篇， 实在太多了，这里有点写不下 orz。

训练结果

最后放上检测结果以及自己训练过程中的 mAP 曲线：

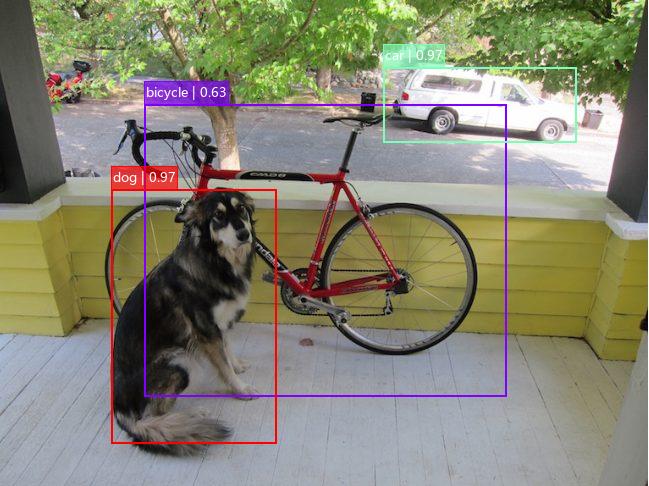
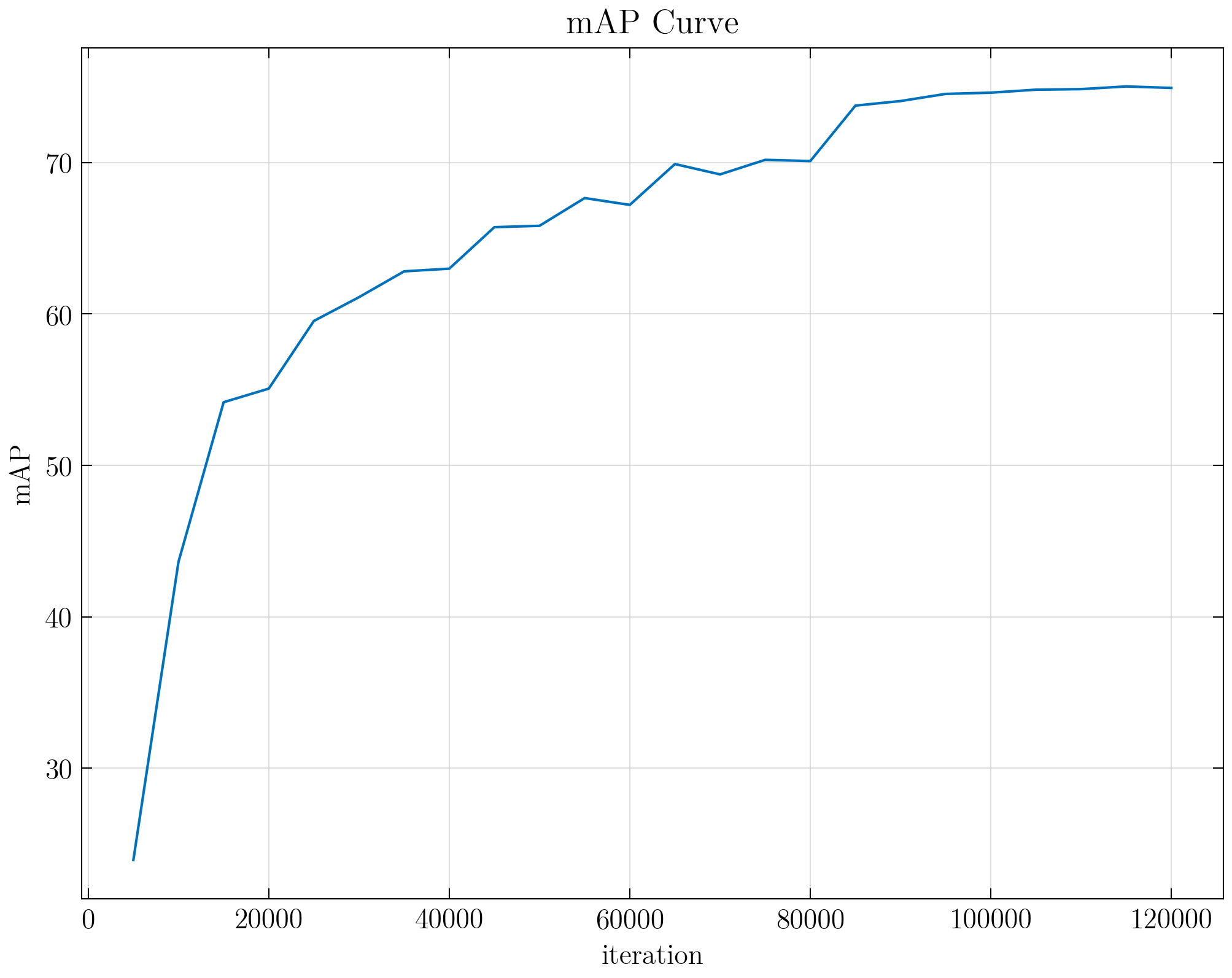
后记

至此 SSD 的原理也介绍的差不多了，至于如何评估模型，大家可以参考别的博客，这里就不赘述了（才不是因为写不动了），代码已经放在了 GitHub 上面，以上~

参考资料

• SSD: Single Shot MultiBox Detector
• SSD 先验框详解
• 目标检测|SSD原理与实现
• 【SSD算法】史上最全代码解析-核心篇
• 【SSD算法】史上最全代码解析-数据篇
• 目标检测-SSD-Single Shot MultiBox Detector-论文笔记