CSP-S2021爆零寄+题解
不想放开头了,考得太难受了/kk
题目
airport
给出 \(m_1\) 个国内航班和 \(m_2\) 个国际航班,其中国内航班只能停在国内廊桥,国际航班只能停在国内廊桥。现在有 \(n\) 个廊桥,给出国内航班和国际航班的到达和离开时间 \(l_i,r_i\),问怎么分配廊桥能使得最多的航班停在廊桥上。(如果停不到廊桥上只能停到远机位不干扰廊桥,对于廊桥的分配采取先到先得原则)。(\(1\le n,m_1+m_2\le 10^5,1\le l_i<r_i\le10^8,\forall i\ne j\) 有 \(l_i\ne l_j,r_i\ne r_j\))
坑死我了...考场写出来正解了,结果因为不 sort 收获了 \(\tt 0pts\)。首先注意到如果一个航班在给这种类型的航班分配 \(k\) 个廊桥时可以停下,则当分配 \(>k\) 个廊桥时依然可以停下。所以这启示了一种前缀和的思想,即先首先算出来当廊桥有无穷个时停下两种类型的航班各需要多少廊桥,再通过枚举分配方案,以前缀和的形式判断当前分配方案下的结果。
具体来讲,我们先把所有航班按照到达时间顺序排序,然后顺序处理,当处理到一个航班时,就把它加到时间最靠前且离开时间小于它的出发时间的廊桥中,并把这个廊桥的离开时间设为它的离开时间,廊桥能承载的飞机数目加一,如果找不到这样的廊桥就新建一个。这样处理可以保证在前缀和的时候找到的方案数是最大的。
如果朴素实现,我们得到的是一个 \(\mathcal{O}(n^2)\) 的复杂度,可以通过 \(\tt 40pts\)。注意到瓶颈在于找到合适的廊桥。发现这个时间最靠前且结束时间小于出发时间的条件可以用二分改为判断一个区间是否有结束时间小于当前航班出发时间的廊桥。那这个就可以用线段树维护区间最小值轻松实现了,如果直接朴素二分套线段树,会收获一个 \(\mathcal{O}(n\log^2 n)\) 的算法,如果直接线段树上二分,会收获一个 \(\mathcal{O}(n\log n)\) 的算法,期望得分均为 \(\tt 100pts\)。
//考场代码,比较丑,能用结构体合并的因为没时间都没合并,但还算能看吧
#include <cstdio>
#include <map>
#include <algorithm>
const int N = 1e5 + 10; struct flt{ int a, b; }f1[N], f2[N];
inline bool cmp(const flt& f1, const flt& f2) { return f1.a < f2.a; }
int tp1, tp2, s1[N], s2[N], sz1[N], sz2[N], tmp[N << 2], tot, m1, m2;
std::map<int, int> mp; int h1[N << 2], h2[N << 2];
inline void pushup1(int k) { h1[k] = std::min(h1[k << 1], h1[k << 1 | 1]); }
void build1(int k, int l, int r)
{
if (l == r) { h1[k] = 2e9; return ; }
int mid = (l + r) >> 1;
build1(k << 1, l, mid); build1(k << 1 | 1, mid + 1, r);
pushup1(k);
}
void change1(int k, int l, int r, int pos, int val)
{
if (l == r) { h1[k] = val; return ; }
int mid = (l + r) >> 1;
if (pos <= mid) change1(k << 1, l, mid, pos, val);
else change1(k << 1 | 1, mid + 1, r, pos, val);
pushup1(k);
}
int query1(int k, int l, int r, int x, int y)
{
if (x <= l && r <= y) return h1[k];
int mid = (l + r) >> 1, ret = 2e9;
if (x <= mid) ret = std::min(ret, query1(k << 1, l, mid, x, y));
if (mid < y) ret = std::min(ret, query1(k << 1 | 1, mid + 1, r, x, y));
return ret;
}
inline void pushup2(int k) { h2[k] = std::min(h2[k << 1], h2[k << 1 | 1]); }
void build2(int k, int l, int r)
{
if (l == r) { h2[k] = 2e9; return ; }
int mid = (l + r) >> 1;
build2(k << 1, l, mid); build2(k << 1 | 1, mid + 1, r);
pushup2(k);
}
void change2(int k, int l, int r, int pos, int val)
{
if (l == r) { h2[k] = val; return ; }
int mid = (l + r) >> 1;
if (pos <= mid) change2(k << 1, l, mid, pos, val);
else change2(k << 1 | 1, mid + 1, r, pos, val);
pushup2(k);
}
int query2(int k, int l, int r, int x, int y)
{
if (x <= l && r <= y) return h2[k];
int mid = (l + r) >> 1, ret = 2e9;
if (x <= mid) ret = std::min(ret, query2(k << 1, l, mid, x, y));
if (mid < y) ret = std::min(ret, query2(k << 1 | 1, mid + 1, r, x, y));
return ret;
}
bool check1(int pos, int val) { return query1(1, 1, m1, 1, pos) < val; }
inline int bfind1(int val)
{
int l = 1, r = tp1, mid, pos = -1;
while (l <= r)
{
mid = (l + r) >> 1;
if (check1(mid, val)) r = mid - 1, pos = mid;
else l = mid + 1;
}
return pos;
}
bool check2(int pos, int val) { return query2(1, 1, m2, 1, pos) < val; }
inline int bfind2(int val)
{
int l = 1, r = tp2, mid, pos = -1;
while (l <= r)
{
mid = (l + r) >> 1;
if (check2(mid, val)) r = mid - 1, pos = mid;
else l = mid + 1;
}
return pos;
}
int main()
{
int n; scanf("%d%d%d", &n, &m1, &m2);
for (int i = 1; i <= m1; ++i) scanf("%d%d", &f1[i].a, &f1[i].b);
for (int i = 1; i <= m2; ++i) scanf("%d%d", &f2[i].a, &f2[i].b);
std::sort(f1 + 1, f1 + m1 + 1, cmp); std::sort(f2 + 1, f2 + m2 + 1, cmp);
build1(1, 1, m1); build2(1, 1, m2);
for (int i = 1, pos; i <= m1; ++i)
{
pos = bfind1(f1[i].a);
if (pos == -1) { change1(1, 1, m1, ++tp1, f1[i].b); ++sz1[tp1]; continue; }
change1(1, 1, m1, pos, f1[i].b); ++sz1[pos];
}
for (int i = 1, pos; i <= m2; ++i)
{
pos = bfind2(f2[i].a);
if (pos == -1) { change2(1, 1, m2, ++tp2, f2[i].b); ++sz2[tp2]; continue; }
change2(1, 1, m2, pos, f2[i].b); ++sz2[pos];
}
for (int i = 1; i <= tp1; ++i) s1[i] = s1[i - 1] + sz1[i];
for (int i = 1; i <= tp2; ++i) s2[i] = s2[i - 1] + sz2[i];
int ans = 0;
for (int i = 0; i <= n; ++i) ans = std::max(s1[i] + s2[n - i], ans);
printf("%d\n", ans); return 0;
}
bracket
定义一种由 (,) 和 * 组成的超级括号串,对于给定的数 \(k\) 合法括号串的形式有且仅有以下几种:
()和(S)是合法的超级括号串,其中S表示一个长度不超过 \(k\) 的非空*串,下同。(A),(AS)和(SA)是合法的超级括号串,其中A表示合法的超级括号串。- 如果
A和B均为合法超级括号串,则AB和ASB是合法的超级括号串。
给出一个长为 \(n\) 的串 \(s\) 和 \(k\),串里面有一些地方不确定,用 ? 表示,求有多少种确定 ? 的方案使得该串为合法的超级括号串,答案对 \(10^9+7\) 取模。(\(1\le k\le n\le500\))
首先看到数据范围,可以想到 \(\mathcal{O}(n^3)\) 的区间 \(\rm dp\)。但如果直接只设一个 \(f_{l,r}\) 表示 \([l,r]\) 区间内可以得到的合法括号串数,直接根据题目转移的话,会无法处理判重问题,具体来讲,考虑这个超级括号串:
(*)*(*)*(*)
它会被这样算两次:
(*)*(*)*(*) -> ASB
A: (*)*(*) S: * B: (*)
A:(*) S: * B: (*)*(*)
而如果我们只对着刚刚定义的状态苦思冥想的话,就会和我一样在考场上浪费光阴。所以我们考虑引入一个新状态帮助判重。注意到题目中的超级括号串分为两类:
- 外层括号匹配上的,有
(),(S),(A),(AS)和(SA)这几种。 - 外层括号匹配不上的,有
AB和ASB这两种。
注意到我们算重的问题就是在 AB 和 ASB 上,如果钦定 B 为外层括号匹配上的字符串,就使得这个 AB 的连接有一定方向性,也就能避免算重的问题了。所以考虑设 \(g_{l,r}\) 表示 \([l,r]\) 区间内外层括号匹配不上的字符串,为了方便转移,我们更改 \(f_{l,r}\) 的定义为 \([l,r]\) 内外层括号匹配上的字符串,并定义 \(h_{l,r}\) 表示 \([l,r]\) 内是否可以全是 *。
我们首先转移 \(f\),转移时先特判掉一些很简单的情况,如果外层括号匹配不上(也就是 \(s_l\) 不能为 ( 或 \(s_r\) 不能为 ))就直接排除,如果能匹配上且长度为 \(2\),则直接考虑 (),给 \(f_{l,r}\) 加一后直接排除。然后挨个考虑如何转移:
(S)先排除掉 \(r-1-l>k\) 的情况(即S的长度大于 \(k\)),接着直接转移:\(f_{l,r}=f_{l,r}+h_{l+1,r-1}\)。(A)直接算A的方案数,即 \(f_{l,r}=f_{l,r}+(f_{l+1,r-1}+g_{l+1,r-1})\)(AS)枚举一下S的长度,有 \(f_{l,r}=f_{l,r}+\sum_{i=1}^k (f_{l+1,r-i-1}+g_{l+1,r-i-1})\times h_{r-i,r-1}\)(SA)跟上面的差不多,有 \(f_{l,r}=f_{l,r}+\sum_{i=1}^k (f_{l+i+1,r-1}+g_{l+i+1,r-1})\times h_{l+1,l+i}\)
\(f\) 的转移就完事了,接下来考虑 \(g\) 的转移。跟上面说的差不多,钦定 B 只能为 \(f\),则有转移 \(g_{l,r}=g_{l,r}+\sum_{l<i<j<r,j-i-1\le k}(f_{l,i}+g_{l,i})\times f_{j,r}\times h_{i+1,j-1}\)。如果我们令 \(h_{x,x-1}=1\),则该转移可以一次处理两种情况。朴素的转移到这里就结束了,最终答案即为 \(f_{1,n}+g_{1,n}\),时间复杂度 \(\mathcal{O}(n^4)\),期望得分 \(\tt 65pts\)。
接下来考虑怎么优化。注意到瓶颈在于 AB 和 ASB 的转移,所以考虑针对这个转移做一些优化。发现 \(i\) 每次移动时,\(j\) 有效的最大值(即既符合求和条件也能使 \(h_{i+1,j-1}=1\))的变化是单调上升的,且最终一共只会增加 \(\mathcal{O}(n)\) 次。考虑把这 \(\mathcal{O}(n)\) 次均摊到 \(i\) 的每次移动,这样就能做到均摊 \(\mathcal{O}(1)\) 移动 \(j\) 了。其实只需要提前求一个 \(nxt\) 数组,其中 \(nxt_x\) 表示当 \(i=x\) 时,\(j\) 的最大值,转移的时候维护一下应该乘的 \(f_{j,r}\) 之和即可。这样最终时间复杂度可以做到 \(\mathcal{O}(n^3)\),期望得分 \(\tt 100pts\)。
#include <cstdio>
const int N = 510, mod = 1e9 + 7;
inline int mo(int x) { return x >= mod ? x -= mod : x; }
char s[N]; int f[N][N], g[N][N], h[N][N], nxt[N];
int main()
{
int n, k; scanf("%d%d%s", &n, &k, s + 1);
for (int l = 1; l <= n; ++l)
{
if (s[l] != '*' && s[l] != '?') continue;
h[l][l] = 1;
for (int r = l + 1; r <= n; ++ r)
{
if (s[r] != '*' && s[r] != '?') break;
h[l][r] = 1;
}
}
for (int len = 2, id, add; len <= n; ++len)
for (int l = 1, r; l + len - 1 <= n; ++l)
{
r = l + len - 1;
if (!(s[l] == '(' || s[l] == '?') || !(s[r] == ')' || s[r] == '?'))
continue;
if (len == 2) { f[l][r] = mo(f[l][r] + 1); continue; }
if (r - 1 - l <= k) f[l][r] = mo(f[l][r] + h[l + 1][r - 1]); // (S)
f[l][r] = mo(f[l][r] + mo(f[l + 1][r - 1] + g[l + 1][r - 1])); // (A)
for (int i = 1; i <= k && l + i < n; ++i) //(SA)
if (h[l + 1][l + i]) f[l][r] = mo(f[l][r] + mo(f[l + i + 1][r - 1] + g[l + i + 1][r - 1]));
for (int i = 1; i <= k && r - i > 1; ++i) //(AS)
if (h[r - i][r - 1]) f[l][r] = mo(f[l][r] + mo(f[l + 1][r - i - 1] + g[l + 1][r - i - 1]));
add = id = 0; //AB & ASB
for (int i = l + 1; i <= r - 2; ++i)
{
if (id <= i) id = i + 1;
while ((s[id] == '*' || s[id] == '?') && id < i + k + 1 && id < r - 1) ++id;
nxt[i] = id;
}
for (int j = l + 2; j <= nxt[l + 1]; ++j) add = mo(add + f[j][r]);
g[l][r] = mo(g[l][r] + 1ll * mo(g[l][l + 1] + f[l][l + 1]) * add % mod);
for (int i = l + 2; i <= r - 2; ++i)
{
add = (add - f[i][r] + mod) % mod;
for (int j = nxt[i - 1] + 1; j <= nxt[i]; ++j) add = mo(add + f[j][r]);
g[l][r] = mo(g[l][r] + 1ll * mo(g[l][i] + f[l][i]) * add % mod);
}
}
printf("%d\n", mo(f[1][n] + g[1][n])); return 0;
}
palin
\(T\) 组数据,每组给定正整数 \(n\) 和整数序列 \(a_1,a_2,\cdot\cdot\cdot,a_{2n}\),其中 \(1\sim n\) 均恰好出现两次。现在进行 \(2n\) 次操作,目标是创建一个同样长为 \(2n\) 的序列 \(b_1,b_2,\cdot\cdot\cdot,b_{2n}\),初始时 \(b\) 为空,每轮操作为以下两种之一:
- 将 \(a\) 的开头元素加到 \(b\) 的末尾,并从 \(a\) 中移除,记为 \(\tt L\)。
- 将 \(a\) 的末尾元素加到 \(b\) 的末尾,并从 \(a\) 中移除,记为 \(\tt R\)。
这样会得到一个长为 \(2n\) 的操作序列。问是否存在一种操作序列使得 \(b\) 最终是回文数列,如果存在则求出字典序最小的操作序列,否则报告无解。(\(1\le T\le 100,1\le n\le5\times10^5,\sum n\le 5\times10^5\))
这题有时间应该能搞出来,可惜我的时间全部砸在了 \(\tt T1,T2\) 上面...... 这道题一看就特别像 CF 和 AT 里面的思维题,所以可以大胆猜一下是个结论。通过手玩大样例,我们可以找到一个规律:
如果有解,则前 \(n\) 次选出来的数形成的序列的 任意前缀,在剩余 \(n\) 个数上面一定是 一段区间。
当然,考场上想到基本可以开始写代码了,不过既然是总结我们还是考虑证明一下吧。前 \(n\) 次选出来的数形成的序列也就是 \(b\) 的前 \(n\) 个数,而这样它的任意前缀即为 \(b\) 的任意前缀,同时由于 \(b\) 是回文,所以也是任意后缀。那这样一定是连续被选择出来添加到末尾的,即一定是一段区间。
好了这道题想出来这个结论基本就结束了,不过实现的细节还是挺多的,所以简单把一些细节说说吧。我们枚举第一次选取的是 \(\tt L\) 还是 \(\tt R\),这样把前缀的基本形态确定出来之后,用个双指针维护一下当前前缀对应的区间,前 \(n\) 次操作能选 \(\tt L\) 就尽量选 \(\tt L\)(这里能选指的是不破坏区间性质),如果 \(\tt L,R\) 均不行直接报告当前枚举到的情况无解即可。如果两种情况都无解直接报告该种情况无解即可,如果存在一种情况有解则直接简单构造一下剩下的 \(n\) 个操作即可,时间复杂度 \(\mathcal{O}(n)\),期望得分 \(\tt 100pts\)。
#include <cstdio>
#include <cstring>
const int N = 5e5 + 10; int a[N << 1], L[N], R[N], b[N]; char ans[N << 1];
int main()
{
int T, n, tp, l, r, head, tail, flag; scanf("%d", &T);
while (T--)
{
scanf("%d", &n); flag = 1;
memset(L, 0, sizeof (L)); memset(R, 0, sizeof (R));
for (int i = 1; i <= (n << 1); ++i)
{
scanf("%d", &a[i]);
!L[a[i]] ? L[a[i]] = i : R[a[i]] = i;
}
ans[tp = 1] = 'L'; b[tp] = a[1]; l = r = R[a[1]]; head = 2; tail = (n << 1);
for (int i = 2; i <= n; ++i)
{
if (R[a[head]] == l - 1 || R[a[head]] == r + 1)
{
ans[++tp] = 'L'; b[tp] = a[head];
(R[a[head]] == l - 1) ? --l : ++r;
++head; continue;
}
if (L[a[tail]] == l - 1 || L[a[tail]] == r + 1)
{
ans[++tp] = 'R'; b[tp] = a[tail];
(L[a[tail]] == l - 1) ? --l : ++r;
--tail; continue;
}
flag = 0; break;
}
if (flag)
{
int len = tp;
for (int i = len; i >= 1; --i)
{
if (a[l] == b[i]) ans[++tp] = 'L', ++l;
else ans[++tp] = 'R', --r;
}
ans[++tp] = '\0'; printf("%s\n", ans + 1); continue;
}
ans[tp = 1] = 'R'; b[tp] = a[n << 1]; l = r = L[a[n << 1]]; head = 1; tail = (n << 1) - 1;
flag = 1;
for (int i = 2; i <= n; ++i)
{
if (R[a[head]] == l - 1 || R[a[head]] == r + 1)
{
ans[++tp] = 'L'; b[tp] = a[head];
(R[a[head]] == l - 1) ? --l : ++r;
++head; continue;
}
if (L[a[tail]] == l - 1 || L[a[tail]] == r + 1)
{
ans[++tp] = 'R'; b[tp] = a[tail];
(L[a[tail]] == l - 1) ? --l : ++r;
--tail; continue;
}
flag = 0; break;
}
if (flag)
{
int len = tp;
for (int i = len; i >= 1; --i)
{
if (a[l] == b[i]) ans[++tp] = 'L', ++l;
else ans[++tp] = 'R', --r;
}
ans[++tp] = '\0'; printf("%s\n", ans + 1); continue;
}
else printf("-1\n");
}
return 0;
}
traffic
有一个由 \(n\) 横 \(m\) 纵直线构成的 \(n\times m\) 个交点的网格图,网格内部的每条边有边权 \(x_1\)。共 \(T\) 组询问,每组询问中会在网格边界向外延申的 \(2\times (n+m)\) 条射线中,有 \(k\) 条上出现了一个有颜色(黑或白)的点,并且给出了这个点到离他最近的网格点之间的边权 \(x_2\),现在你需要将整个网格黑白染色,使得相邻不同色点之间的边权和最小,输出这个最小值。(\(2\le n,m\le500,1\le T\le50,1\le k_i\le \min(2(n+m),50),1\le\sum k_i\le 50,0\le x_1,x_2\le10^6\),题意来自 ix35 的博客,有简单删改)
这题难度对我来讲很大/kk 所以打算分四档
暴力
很简单的 \(\rm dfs\) 想法,但如果直接朴素 \(\rm dfs\),就会得到一个 \(\mathcal{O}(nm2^{nm})\) 的朴素做法,显然不足以通过本题的暴力分数。不过如果在 \(\rm dfs\) 的时候就顺便算一下非附加点对应边的权值和,再加点剪枝,就能得到 \(\mathcal{O}(k2^{nm})\) 的做法,足以获得 \(\tt 10pts\) 的好成绩。代码是跟下文的最小割部分分放在一起的。
最小割——Dinic
注意到题目中的问题其实相当于把原图分成黑白两个连通块,并问它们割的最小值。这显然就是一个最小割能解决的问题了。考虑建超级源汇,超级源点指向所有白色点,超级汇点指向所有黑色点。并连上网格图对应的边,最终答案即为该图的最小割。但是考虑到数据范围很大,这样的做法并不足以通过全部的测试点,具体分数跟实现有关。我的大常数实现可以获得 \(\tt 60pts\) 的好成绩。
#include <queue>
#include <cstdio>
#include <cstring>
#define id(x, y) ((x - 1) * m + y)
const int K = 510, N = K * K, M = N << 4;
typedef long long ll; const ll inf = 1e16; int d[N], s, t;
struct edge{ int v, next; ll c; }E[M], TE[M]; int p[N], tp[N], cur[N], cnt;
inline void init() { memset(p, -1, sizeof (p)); cnt = 0; }
inline void insert(int u, int v, ll c) { E[cnt].v = v; E[cnt].c = c; E[cnt].next = p[u]; p[u] = cnt++; }
inline void addedge(int u, int v, ll c) { insert(u, v, c); insert(v, u, 0); }
inline bool bfs()
{
memset(d, -1, sizeof (d)); d[s] = 0; cur[s] = p[s];
std::queue<int> q; q.push(s); int u;
while (!q.empty())
{
u = q.front(); q.pop();
for (int i = p[u], v; i + 1; i = E[i].next)
{
v = E[i].v; cur[v] = p[v];
if (d[v] == -1 && E[i].c) { d[v] = d[u] + 1; q.push(v); }
}
}
return d[t] != -1;
}
ll dfs(int u, ll flow)
{
if (u == t) return flow; ll ans = 0, ret;
for (int i = cur[u], v; i + 1; i = E[i].next)
{
v = E[i].v; cur[u] = i;
if (E[i].c && d[v] == d[u] + 1)
{
ret = dfs(v, std::min(flow, E[i].c));
E[i].c -= ret; E[i ^ 1].c += ret;
ans += ret; flow -= ret; if (!flow) break;
}
}
if (!ans) d[u] = -1;
return ans;
}
inline ll dinic() { ll ans = 0; while (bfs()) ans += dfs(s, inf); return ans; }
int main()
{
init(); int n, m, T; scanf("%d%d%d", &n, &m, &T); s = 0; t = id(n, m) + 1;
for (int i = 1, x; i < n; ++i)
for (int j = 1; j <= m; ++j)
{
scanf("%d", &x);
addedge(id(i, j), id(i + 1, j), x);
addedge(id(i + 1, j), id(i, j), x);
}
for (int i = 1, x; i <= n; ++i)
for (int j = 1; j < m; ++j)
{
scanf("%d", &x);
addedge(id(i, j), id(i, j + 1), x);
addedge(id(i, j + 1), id(i, j), x);
}
int tcnt = cnt; memcpy(tp, p, sizeof (p)); memcpy(TE, E, sizeof (E));
while (T--)
{
int k; scanf("%d", &k);
for (int i = 1, x, p, typ, pos; i <= k; ++i)
{
scanf("%d%d%d", &x, &p, &typ);
if (p >= 1 && p <= m) pos = id(1, p);
else if (p > m && p <= m + n) pos = id(p - m, m);
else if (p > m + n && p <= 2 * m + n) pos = id(n, 2 * m + n + 1 - p);
else pos = id(2 * m + 2 * n + 1 - p, 1);
typ ? addedge(s, pos, x) : addedge(pos, t, x);
}
printf("%lld\n", dinic());
cnt = tcnt; memcpy(p, tp, sizeof (p)); memcpy(E, TE, sizeof (E));
}
return 0;
}
最小割——对偶图
如果您做过 P4001 [ICPC-Beijing 2006]狼抓兔子 这道题的话,就会知道一个重要的定理:平面图最小割等于对偶图最短路。如果没做过的话也没关系,简单解释一下对偶图就是对平面图上每一个被单独分出来的平面新建一个点,并在有直接边相隔的两个点之间建一条边权为相隔那条边边权的无向边。则从 \(s\) 到 \(t\) 的最小割就等于其在对偶图上对应的最短路。可能说的有点抽象,就以狼抓兔子那道题举个例子吧:
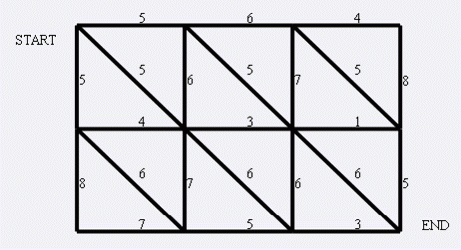
这张平面图对应的对偶图即为:
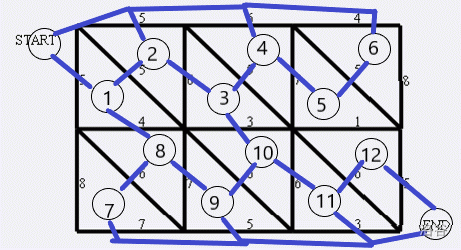
其中每条蓝边边权为其覆盖的那条黑边的边权。证明也很显然,因为走一条路相当于割掉了这条边,从 \(s\) 走到 \(t\) 割掉的边集就足以让 \(s,t\) 不连通,最短路保证了这是最小割。
那言归正传,对于这道题也显然可以采取这种方法建出来对偶图。但是非常遗憾的是,数据范围里的 \(k\) 并不是 \(k\le 2\) 的,也就是说,可能会出现多源汇相互匹配的情况。只单纯做简单的最短路只能获得 \(k\le 2\) 的部分分,加上暴力的 \(\tt10pts\),总共可以收获 \(\tt 55pts\) 的好成绩。代码非常长,贴 link 了。
正解
就像我们在刚刚单纯最短路部分分中思考的那样,这题 \(k>2\) 的情况本质上是多源汇匹配的问题,也即每个黑点要匹配一个白点。(可以证明如果不这样匹配答案会劣,但是我不会...)因为是环形的问题,所以我们要破坏为链,在两倍的序列上匹配。注意到其实一段连续的黑点或白点其实就相当于一个黑或白点,因为它们完全可以构成一个黑或白连通块,所以我们完全可以把原序列处理成黑白相间的。考虑设 \(f_{l,r}\) 表示区间 \([l,r]\) 已经完成匹配能获得的最小代价和。则转移的时候有两种选择:要么选择 \(d_l,d_r\) 匹配,从 \(f_{l+1,r-1}\) 转移过来,要么枚举一个中间结点 \(mid\),把区间 \([l,mid],(mid,r]\) 合并,即从 \(f_{l,mid},f_{mid+1,r}\) 转移过来。具体来讲有:
其中 \(d_l,d_r\) 表示点 \(d_l,d_r\) 对应到我们摊平的区间上编号为 \(l,r\)(也可以理解为离散化了一下吧)。\(dis_{i,j}\) 表示 \(i\) 点匹配 \(j\) 点的代价,如果 \(i,j\) 颜色相同,则 \(dis_{i,j}=\infty\)(不过事实上,经过上述黑白相间的处理,\(d_l,d_r\) 不可能出现颜色相同的情况)。这样我们从所有白点跑一遍单源最短路就可以求出 \(dis\) 数组,然后再 \(\mathcal{O}(k^3)\) 做上述区间 \(\rm dp\),最后答案就是所有长度为 \(k\) 的区间最小值(即 \(\min_{i=1}^k \{f_{i,i+k-1}\}\))。总的时间复杂度为 \(\mathcal{O}(\sum k^3+nm\log nm\sum k)\),足以通过本题,收获 \(\tt 100pts\) 的好成绩。
#include <queue>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define id(x, y) ((x - 1) * m + y)
const int K = 510, N = K * K, M = N << 4;
typedef long long ll; const ll inf = 1e15;
struct edge{ int v, next; ll w; }E[M]; int p[N], cnt, tcnt;
inline void init() { memset(p, -1, sizeof (p)); cnt = 0; }
inline void insert(int u, int v, ll w) { E[cnt].v = v; E[cnt].w = w; E[cnt].next = p[u]; p[u] = cnt++; }
std::priority_queue<std::pair<ll, int> > pq; ll dis[N]; int vis[N];
inline void dijkstra(int s)
{
memset(dis, 0x3f, sizeof (dis)); memset(vis, 0, sizeof (vis));
while (!pq.empty()) pq.pop(); dis[s] = 0; pq.emplace(0, s); int u;
while (!pq.empty())
{
u = pq.top().second; pq.pop(); if (vis[u]) continue; vis[u] = 1;
for (int i = p[u], v; i + 1; i = E[i].next)
{
v = E[i].v;
if (dis[v] > dis[u] + E[i].w && !vis[v])
{
dis[v] = dis[u] + E[i].w;
pq.emplace(-dis[v], v);
}
}
}
}
ll cost[K][K], f[K][K]; int n, m, q;
ll work(int k)
{
memset(f, 0x3f, sizeof (f)); int n = k << 1;
auto g = [k](int x) { return (x - 1) % k + 1; }; //把环上 (k,2k] 的点对应到 [1,k]
for (int i = 1; i < n; ++i) f[i][i + 1] = cost[g(i)][g(i + 1)]; //处理边界情况
for (int len = 4; len <= k; len += 2) //因为只能两两匹配,所以区间长度只有偶数
for (int l = 1; l + len - 1 <= n; ++l)
{
int r = l + len - 1;
f[l][r] = f[l + 1][r - 1] + cost[g(l)][g(r)];
for (int mid = l + 1; mid < r; ++mid)
f[l][r] = std::min(f[l][r], f[l][mid] + f[mid + 1][r]);
}
ll res = inf;
for (int i = 1; i <= k; ++i) res = std::min(res, f[i][i + k - 1]);
return res;
}
struct EX{ int eid, c; ll w; }pnt[K]; int st[K], ed[K], sta[K], rk[N << 2], tp, ts, te;
inline void query()
{
ts = te = tp = 0; for (int i = 0; i < tcnt; ++i) E[i].w = 0; //多测清空
int k; scanf("%d", &k);
for (int i = 1; i <= k; ++i) scanf("%lld%d%d", &pnt[i].w, &pnt[i].eid, &pnt[i].c),
E[(pnt[i].eid - 1) << 1].w = E[(pnt[i].eid - 1) << 1 | 1].w = pnt[i].w;
std::sort(pnt + 1, pnt + k + 1, [&](const EX& a, const EX& b) { return a.eid < b.eid; });
if (pnt[1].c == 1 && pnt[k].c == 0) st[++ts] = pnt[1].eid, sta[++tp] = pnt[1].eid;
else if (pnt[1].c == 0 && pnt[k].c == 1) ed[++te] = pnt[1].eid, sta[++tp] = pnt[1].eid;
for (int i = 2; i <= k; ++i)
{
if (pnt[i].c == 1 && pnt[i - 1].c == 0) st[++ts] = pnt[i].eid, sta[++tp] = pnt[i].eid;
else if (pnt[i].c == 0 && pnt[i - 1].c == 1) ed[++te] = pnt[i].eid, sta[++tp] = pnt[i].eid;
} //这一部分实际上就是把序列处理成黑白相间的
std::sort(sta + 1, sta + tp + 1);
for (int i = 1; i <= tp; ++i) rk[sta[i]] = i; //离散化一下
if (!ts) return printf("0\n"), void();
memset(cost, 0x3f, sizeof (cost));
for (int i = 1; i <= ts; ++i)
{
dijkstra(st[i]);
for (int j = 1; j <= te; ++j) //对于每个点跑单源最短路,处理 cost (也就是上述的 dis
cost[rk[st[i]]][rk[ed[j]]] = cost[rk[ed[j]]][rk[st[i]]] = dis[ed[j]];
}
printf("%lld\n", work(ts << 1));
}
int main()
{
init(); scanf("%d%d%d", &n, &m, &q); ll x;
for (int i = 1; i < ((n + m) << 1); ++i)
insert(i, i + 1, 0), insert(i + 1, i, 0);
insert((n + m) << 1, 1, 0); insert(1, (n + m) << 1, 0);
int d = (n + m) << 1; tcnt = cnt;
for (int i = 1; i < n; ++i)
for (int j = 1; j <= m; ++j)
{
scanf("%lld", &x);
if (j == 1)
insert(((m + n) << 1) + 1 - i, d + id(i, j), x),
insert(d + id(i, j), ((m + n) << 1) + 1 - i, x);
else if (j == m)
insert(m + 1 + i, d + id(i, j - 1), x),
insert(d + id(i, j - 1), m + 1 + i, x);
else
insert(d + id(i, j - 1), d + id(i, j), x),
insert(d + id(i, j), d + id(i, j - 1), x);
}
for (int i = 1; i <= n; ++i)
for (int j = 1; j < m; ++j)
{
scanf("%lld", &x);
if (i == 1)
insert(1 + j, d + id(i, j), x),
insert(d + id(i, j), 1 + j, x);
else if (i == n)
insert(2 * m + n + 1 - j, d + id(i - 1, j), x),
insert(d + id(i - 1, j), 2 * m + n + 1 - j, x);
else
insert(d + id(i - 1, j), d + id(i, j), x),
insert(d + id(i, j), d + id(i - 1, j), x);
}
while (q--) query(); return 0;
}
总结
更新的这一天真长
这次考试算是大失败了吧,不管是在考试策略还是最终反映到的结果上。\(\tt T1,2,3\) 题考的几乎都是思维,除了 \(\tt T2\) 中对于括号序列分类的去重套路。这是近年考题的大方向,感觉加强了 AT 和 CF 上一些思维题的重要性。应对这种题,最重要的是要找到题目内新操作或新名词之类的特点,再用这些特点去解题,效率会大大提高。而 \(\tt T4\) 中对于最小割和对偶图的转化是对比较难的图论的考查,说明近年的考题会逐年攀升,网络流之类的知识点会逐渐下放,这就要求知识点的掌握不能有漏洞,所有知识点都要有所涉及。而考试策略,一定要先把暴力打好,不但会方便对拍,也能稳定自己的心理,毕竟手里拿到分了。对于长时间写不出来的题就不要纠结了,牢记 CCF 的开题顺序不一定就是题号顺序,多往后看看。

