CSP-S2019做题总结
哈哈了,六道题一半是靠题解订出来的,格雷码就是来平衡难度的...
题目
[CSP-S2019] 格雷码
当时初二,唯一一道考场 AC 。
我们定义 \(n+1\) 位格雷码,由 \(n\) 位格雷码的 \(2^n\) 个二进制串按顺序排列再加前缀 \(0\),和按逆序排列再加前缀 \(1\) 构成,共 \(2^{n+1}\) 个二进制串。另外,对于 \(n\) 位格雷码中的 \(2^n\) 个二进制串,我们按上述算法得到的排列顺序将它们从 \(0 \sim 2^n-1\) 编号。给出 \(n,k\) ,求按上述算法生成的 \(n\) 位格雷码中的 \(k\) 号二进制串。(\(1\le n\le64,0\le k<2^n\))
题目已经明示了递归结构,如果我们设 \(f_{n,k}\) 表示 \(n\) 位格雷码串的 \(k\) 号二进制串,则有
那个 \(2^{n-1}-(k-2^{n-1}+1)\) 其实就是 \(k\) 去掉前面一半后再逆序得到的结果,除了这点应该没啥难理解的。唯一要注意的是不能把式子合并为 \(2^n-k-1\) ,不然当 \(n=64\) 的时候就没了。时间复杂度 \(\mathcal{O}(n)\) 。感谢毒瘤出题人没在这题 再 放个高精度。
#include <cstdio>
typedef unsigned long long ull;
inline void work(int n, ull k)
{
//注意这里是1ull,不然1默认是int类型,右移64位就溢出了
if (n == 0) return ; ull len = 1ull << (n - 1);
if (k <= len - 1) putchar('0'), work(n - 1, k);
else putchar('1'), work(n - 1, len - k + len - 1);
}
int main()
{
int n; ull k; scanf("%d%llu", &n, &k);
work(n, k); putchar('\n'); return 0;
}
[CSP-S2019] 括号树
还算是正常的 tgT2 难度,只不过当时太菜了 (现在也是) 只会暴力。
给出一棵 \(n\) 个结点的树,每个结点上有一个括号 ( 或 ) ,定义 \(k_i\) 表示从根节点到 \(i\) 的路径上括号串所有子串中有多少个合法括号序列(合法括号序列和子串定义同一般定义)。(\(1\le n\le 5\times10^5\))
因为子串这东西不好找,而注意到根结点到结点 \(i\) 的路径上所有合法括号序列子串其实就是以路径上所有结点结尾的合法序列数量之和,所以我们可以定义 \(f_i\) 表示树上以 \(i\) 结尾的合法括号序列个数,最后统计答案的时候树上前缀和一下就好。接下来就考虑如何求出 \(f_i\) 。
我们来形式化定义一下合法括号序列。如果设 ( 表示 \(1\) ,) 表示 \(-1\) ,\(s_i\) 表示前缀和,则序列 \(a_{l..r}\) 是合法序列当且仅当:
- \(s_l=s_r\)
- \(\forall l\le i\le r,s_i\ge s_l\)
如果我们设 \(c_s\) 表示当前路径中 \(s\) 出现的次数,则去掉当前结点的次数, \(c_s\) 其实就是当前结点满足 1 条件的序列个数。而考虑 2 条件的限制,我们定义 \(las_s\) 表示 \(s\) 上一次出现时候的值,只要减去 \(las_{s-1}\) 上的 \(c_s\),即最后一个不合法的位置上 \(c_s\) 的值就得到了满足 1,2 两个条件的序列个数。我们 \(\rm dfs\) 一遍序列,可以维护上面所述的过程,但条件 2 不好找,我们可以用 \(\rm vector\) 记录一下,之后等回溯的时候再处理(详见代码),最后前缀和一下,处理处理输出就好了,时间复杂度 \(\mathcal{O}(n)\) 。
#include <cstdio>
#include <vector>
#include <cstring>
const int N = 5e5 + 10; typedef long long ll;
int las[N << 1], c[N << 1]; char s[N]; ll ans[N], Ans;
struct edge{ int v, next; }E[N << 1]; int p[N], cnt; std::vector<int> vec[N];
inline void init() { memset(p, -1, sizeof (p)); cnt = 0; }
inline void insert(int u, int v) { E[cnt].v = v; E[cnt].next = p[u]; p[u] = cnt++; }
void dfs(int u, int sum)
{
sum += s[u] == '(' ? 1 : -1; ans[u] = c[sum]++;
int last = las[sum]; las[sum] = u; vec[las[sum - 1]].push_back(u);
for (int i = p[u], v; i + 1; i = E[i].next) v = E[i].v, dfs(v, sum);
for (int i = 0; i < vec[u].size(); ++i) ans[vec[u][i]] -= c[sum + 1];
--c[sum]; las[sum] = last;
}
void dfs(int u)
{ for (int i = p[u], v; i + 1; i = E[i].next) { v = E[i].v; ans[v] += ans[u]; dfs(v); } }
int main()
{
init(); int n; scanf("%d%s", &n, s + 1); c[n + 1] = 1;
for (int i = 2, fa; i <= n; ++i) scanf("%d", &fa), insert(fa, i);
dfs(1, n + 1); dfs(1); for (int i = 1; i <= n; ++i) Ans ^= (i * ans[i]);
printf("%lld\n", Ans); return 0;
}
[CSP-S2019] 树上的数
D1T3 开始不正常起来了,从此 CSP-S2019 在神题的路上一去不复返了。
给一棵有 \(n\) 个结点的树,树上每个结点上有一个数 \(a_i\) 且满足 \(a\) 是一个 \(1\sim n\) 的排列。接下来要进行恰好 \(n-1\) 次删边,每次操作要选择一条未被删去的边,交换边连接两点上面的数字并删去这条边。当所有的边都被删去后,将数字按照从 \(1\sim n\) 的顺序依次排列得到一个排列 \(\mathcal{P}\) ,求出在最优操作方案下得到的字典序最小的 \(\mathcal{P}\) 。(\(1\le n\le 2000\))
看了两个晚上的神仙思维题。这题直接突破太难了,所以我们慢慢考虑部分分。
暴力
如果你考场上成功打出了 \(\mathcal{O}(n!n)\) 之类的嗯暴力,收获了 \(\tt 10pts\) ,恭喜你收获了考场满分。这一部分比较简单就不放代码和讲解了。
菊花图
这题菊花图的部分分是比链的好想的,大概是因为菊花图对应的路径都比较短。
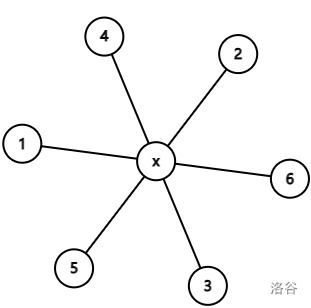
比如这个菊花图,我们假设删边顺序是 \((u_1,x),(u_2,x),(u_3,x),(u_4,x),(u_5,x),(u_6,x)\) ,则手玩一下可以发现 \(a_x\) 移动到 \(a_{u_1}\) ,\(a_{u_1}\) 移动到 \(a_{u_2}\) ,\(a_{u_2}\) 移动到 \(a_3\) 以此类推。我们可以贪心构造这个顺序,从 \(1\sim n\) 枚举每一个数,每次贪心选取删边顺序的下一条边,该数字最后的位置就是该边对应的 \(u_i\) 。
链
链的关系中,我们就要分析边与边之间的关系了,如果一个数字 \(k\) 想从初始位置 \(u_1\) 移动到 \(u_m\) ,则路径上的点 \(u_1,u_2,\cdot\cdot\cdot,u_m\) 上要有以下性质:
- 对于起点 \(u_1\),其出边 \((u_1,u_2)\) 一定是先被删掉的边。
- 对于结尾点 \(u_m\),其入边 \((u_{m-1},u_m)\) 一定是这一点最后被删除的边。
- 对于中间点 \(u_i\) ,其入边 \((u_{i-1},u_i)\) 先于出边 \((u_i,u_{i+1})\) 被删。
我们对于每个点的出入边可以获得一个删边的顺序,依然按 \(1\sim n\) 枚举每个点,检查每个数字从初始位置从左到右走的点中的最小编号。这个点不能走,当且仅当该点的顺序已确定且不满足需求的顺序。
正解
跟链类似,将一个数字 \(k\) 从初始位置 \(u_1\) 移动到 \(u_m\) ,在路径上的点 \(u_1,u_2,\cdot\cdot\cdot,u_m\) :
- 对于起点 \(u_1\),其出边 \((u_1,u_2)\) 一定是这一点第一条被删掉的边。如果不是的话 \(k\) 就会被换到其他点上。
- 对于终点 \(u_m\),其入边 \((u_{m-1},u_m)\) 一定是这一点最后一条被删除的边。如果不是,\(k\) 也会被换到其他点上。
- 对于中间点 \(u_i\) ,其入边 \((u_{i-1},u_i)\) 先于出边 \((u_i,u_{i+1})\) 被删,且在该点的所有边里被删除的顺序是相邻的。如果不满足后一条性质,\(k\) 在中间会被换到其他点上。
注意到这些限制其实都是限制在某一点的边上的,所以我们可以单独考虑每个点的情况,依然是 \(1\sim n\) 枚举每个数字,从这个数字的初始位置开始 \(\rm dfs\) ,依次检查路径上的点是否可以作为中间点或者终点即可。
明白了这点之后,这题就差不多.....刚开始了。因为实现检查每个点是否满足中间点或终点的条件非常繁琐。我这边用的是链表和并查集的实现,其中链表管理某个点的边是否被应用了 在某边之后或之前被删 的限制,并查集管理某个点的边的限制形成的链式结构,且用两个数组 \(beg,end\) 储存某个点的所有边中,被 固定 为第一条或最后一条被删的边。
对于一个点,它能作为终点的条件为:
- 不是起点。
- 入边必须能作为该点的最后一条被删的边。
- 当该点度数为 \(1\) 时最后一条和第一条被删的边为同一条。
对于一个点,它能作为中间点的条件为:
- 入边之后不能有除出边外紧接着要删掉的边。
- 出边之前不能有除入边外紧接着要删掉的边。
- 将入边和出边的限制关系加入后,如果会使该点的第一条和最后一条被删的边加入了同一条关系链,则此时该点的所有边都在这条关系链中。
根据以上条件判断一个点是否能作为中间点或者终点,寻找每个数字的最小编号终点,之后在路径上应用出入边的限制即可,具体细节塞到代码注释惹。最终时间复杂度 \(\mathcal{O}(n^2)\) ,但因为大常数,所以过 \(n\le 2000\) 都勉强。
#include <cstdio>
#include <cstring>
#include <algorithm>
inline void read(int& x)
{
x = 0; char ch; int f = 1;
while ((ch = getchar()) < '0' || ch > '9')
f = (ch ^ '-' ? 1 : -1);
while (x = (x << 1) + (x << 3) + ch - '0',
(ch = getchar()) >= '0' && ch <= '9') ;
x *= f;
}
//beg,end 每个点对应的最先/最后被删的边
const int N = 2e3 + 10; int pnt[N], beg[N], end[N], deg[N], T, n;
struct edge{ int v, next; }E[N << 1]; int p[N], cnt;
inline void insert(int u, int v) { E[cnt].v = v; E[cnt].next = p[u]; p[u] = cnt++; }
struct DSU
{
int f[N]; bool pre[N], nxt[N]; //pre,nxt 一条边是否确定了前后关系
void clear()
{
memset(pre, 0, sizeof (pre)); memset(nxt, 0, sizeof (nxt));
for (int i = 1; i <= n; ++i) f[i] = i;
}
int getf(int x) { return x == f[x] ? x : f[x] = getf(f[x]); }
void merge(int x, int y)
{
int tx = getf(x), ty = getf(y);
f[ty] = tx; nxt[x] = pre[y] = true;
}
bool same(int x, int y) { return getf(x) == getf(y); }
}dsu[N];
inline void init()
{
memset(beg, 0, sizeof (beg)); memset(end, 0, sizeof (end));
memset(deg, 0, sizeof (deg)); memset(p, -1, sizeof (p)); cnt = 0;
for (int i = 1; i <= n; ++i) dsu[i].clear();
}
int dfs(int u, int fa)
{
int mn = n + 1;
//fa != 0: 不是起点 | end[u] == 0 || end[u] == fa 入边是最后删的边
//!dsu[u].nxt[fa] 入边之后必须再无删边
//!(beg[u] != 0 && deg[u] > 1 && dsu[u].same(fa, beg[u]))
//^入边和最后删边不在同一条关系链中,最后一条链时除外^
if (fa != 0 && (end[u] == 0 || end[u] == fa) && !dsu[u].nxt[fa] &&
!(beg[u] != 0 && deg[u] > 1 && dsu[u].same(fa, beg[u]))) mn = std::min(mn, u);
//^尝试以 u 点作为终点^
for (int i = p[u], v; i + 1; i = E[i].next)
{
v = E[i].v; if (v == fa) continue;
if (fa == 0) //尝试以 v 作为起点之后的点
{
if (beg[u] != 0 && beg[u] != v) continue; //如果起点最后删掉的边不是这条不行
if (dsu[u].pre[v]) continue; //如果这条边删之前有必须删的边不行
if (end[u] != 0 && deg[u] > 1 && dsu[u].same(v, end[u])) continue;
//^如果这条边与最后删边在同一关系链中且仍有未加入关系链的边不行^
mn = std::min(mn, dfs(v, u));
}
else //尝试以 v 作为路径中的点
{
if (fa == end[u] || v == beg[u] || dsu[u].same(fa, v)) continue;
//^如果入边是最后删边,出边是最先删边,出入边已经在同一条关系链中不行^
if (dsu[u].pre[v] || dsu[u].nxt[fa]) continue;
//^出边之前必须删边,入边之后必须删边则不行^
if (beg[u] != 0 && end[u] != 0 && deg[u] > 2 &&
dsu[u].same(fa, beg[u]) && dsu[u].same(v, end[u])) continue;
//^如果这样出入边会导致最先删边和最后删边在同一关系链且仍有其他边没在关系链中不行^
mn = std::min(mn, dfs(v, u));
}
}
return mn;
}
bool modify(int u, int fa, int tar)
{
if (u == tar) { end[u] = fa; return true; }
for (int i = p[u], v; i + 1; i = E[i].next)
{
v = E[i].v; if (v == fa) continue;
if (!modify(v, u, tar)) continue;
if (fa == 0) beg[u] = v; //这条边是起点
else dsu[u].merge(fa, v), --deg[u]; //这条边是中间的点
return true;
}
return false;
}
int main()
{
read(T);
while (T--)
{
read(n); init(); for (int i = 1; i <= n; ++i) read(pnt[i]);
for (int i = 1, x, y; i < n; ++i)
{
read(x); read(y); insert(x, y); insert(y, x);
++deg[x]; ++deg[y];
//^deg 表示一个点的边关系构成链的数量,初始时为度数,之后每加入一个关系减一^
}
for (int i = 1, x; i <= n; ++i) //先确定优先级更高的结点
{
x = dfs(pnt[i], 0); //找到能找到的终点最小值
modify(pnt[i], 0, x); //之后更新边的链关系
printf("%d ", x);
}
printf("\n");
}
return 0;
}
[CSP-S2019] Emiya 家今天的饭
为啥 D2T1 会考一道计数 \(\rm dp\) 啊(恼),组合数学永远的痛。
给出一个 \(n\) 行 \(m\) 列的表格,每个格子上有 \(a_{i,j}\) 个棋子,现在要在其中选出 \(k\) 个棋子,满足以下条件:
- \(k \ge 1\) 。
- 每一行只能取一个。
- 每一列至多取 \(\left\lfloor\dfrac{k}{2}\right\rfloor\) 个。
求所有满足条件的取法方案数,答案对 \(998,244,353\) 取模。(\(1\le n\le 100,1\le m\le 2000,0\le a_{i,j}<998,244,353\))
首先发现,前两个限制容易考虑,而最后一个限制不是很好直接计算,所以考虑容斥最后一个限制,即把最终的答案转化为 每行取一个的方案数 - 每行取一个方案数且存在一列取超过一半的方案数 。我们分别 \(\rm dp\) 即可。
首先处理总方案数,设 \(g_{i,j}\) 为前 \(i\) 行取了 \(j\) 个的方案数,则显然有转移,即枚举选还是不选,其中 \(s_i\) 表示第 \(i\) 行 \(a_{i,j}\) 的和,下同:
\(\mathcal{O}(n^2)\) 直接转移即可。
接下来考虑存在一列超过一半的方案数。可以发现,如果存在这样的一列,则其余列必不可能超过一半,正确性显然。则我们枚举哪一列超过了限制,其余列怎么选对方案的合理性就没有影响了,所以我们枚举一个超过限制的列 \(col\) ,并设 \(f_{i,j,k}\) 表示前 \(i\) 行,在 \(col\) 列选了 \(j\) 个,在其余列选了 \(k\) 个的方案数,则显然有转移:
最终方案数就是 \(\sum_{j>k}f_{n,j,k}\) 。如果直接朴素转移,复杂度为 \(\mathcal{O}(mn^3)\) ,只能收获 \(\tt 84pts\) 。考虑优化转移。
注意到在最终统计答案时,我们并不关心 \(j,k\) 的具体值,而关注的是 \(j,k\) 的大小关系,所以我们可以压缩一维状态,设 \(f_{i,j}\) 表示前 \(i\) 行中在枚举到的 \(col\) 列选的数量比其余列多 \(j\) 个,则转移变为:
注意到 \(j\) 可能小于 \(0\) ,为了避免 \(\tt RE\) 要处理一下。最终方案数就是 \(\sum_{j>0}f_{n,j}\) ,复杂度为 \(\mathcal{O}(mn^2)\) ,即为最终复杂度,足以通过本题。
#include <cstdio>
#include <cstring>
typedef long long ll;
const int N = 105, M = 2005, mod = 998244353;
int f[N][N << 1], g[N][N], a[N][M], s[N];
int main()
{
int n, m, s1 = 0, s2 = 0; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
scanf("%d", &a[i][j]), s[i] = (s[i] + a[i][j]) % mod;
for (int col = 1; col <= m; ++col)
{
memset(f, 0, sizeof (f)); f[0][n] = 1;
for (int i = 1; i <= n; ++i)
for (int j = n - i; j <= n + i; ++j)
f[i][j] = (f[i - 1][j] + (!j ? 0 : (ll)a[i][col] * f[i - 1][j - 1] % mod) +
(ll)(s[i] - a[i][col]) * f[i - 1][j + 1] % mod) % mod;
for (int j = 1; j <= n; ++j) s2 = (s2 + f[n][n + j]) % mod;
}
g[0][0] = 1;
for (int i = 1; i <= n; ++i)
for (int j = 0; j <= n; ++j)
g[i][j] = (g[i - 1][j] + (!j ? 0 : (ll)s[i] * g[i - 1][j - 1] % mod)) % mod;
for (int i = 1; i <= n; ++i) s1 = (s1 + g[n][i]) % mod;
printf("%d\n", (s1 - s2 + mod) % mod); return 0;
}
[CSP-S2019] 划分
还记得格雷码的 再 吗,伏笔回收,这题毒瘤高精度。
给出一个长为 \(n\) 的序列 \(a\) ,找到一些分界点 \(1\le k_1<k_2<\cdot\cdot\cdot<k_p<n\),使得
注意 \(p\) 可以等于 \(0\) ,此时表示不分开。在此基础上,最小化
求出这个最小值。(\(2\le n\le4\times10^7,1\le a_i\le10^9\))
但凡出题人让对某个数取模.jpg 首先根据均值不等式的知识,我们知道:
这启示我们如果能划分就要尽量划分,这样才能使最终的结果最小,也就是说每次划分要使得划分的最后一段最短。通过这个思路,我们很自然想到 \(\rm dp\) ,我们设 \(f_{i}\) 以 \(i\) 结尾的划分序列的最小代价,则有贪心转移:
其中 \(las_i\) 表示以 \(i\) 结尾的划分段之和,\(s_i\) 表示前缀和,最终答案即为 \(f_n\) 。但显然 \(\mathcal{O}(n^2)\) 的转移不足以通过这道数据范围及其毒瘤的题,所以考虑优化。注意到这个形式非常像滑动窗口,且时间复杂度要求 \(\mathcal{O}(n)\) ,所以考虑单调队列优化。
如果我们设 \(g_i\) 表示划分段结尾为 \(i\) 时上一个划分段的末尾,则根据之前所说的最后一段最短,\(g_i\) 即为:
移项,有:
令 \(f(x)=2s_x-s_{g_x}\) ,则 \(g_i=\max_{pos=1}^{i-1}pos[f(pos)\le s_i]\) 。如果 \(x,y\) 满足\(f(x),f(y)\le s_i\) ,且 \(x<y\) ,则 \(x\) 无论如何都不会成为 \(g_i\) 。这样我们就导出了单调队列的思路。
单调队列其实就两个部分,一个是处理过时决策,一个是入队维护单调性。首先看处理过时决策,因为 \(s_i\) 是单调递增的,所以如果队头 \(head\) 的下一位 \(next\) 都满足 \(f(next)\le s_i\) 的话,因为 \(next\) 比 \(head\) 晚进队,即 \(next \ge head\) ,所以可以直接弹出队首。它可能在之前 \(s_i\) 较小时是最优解,但当 \(s_i\) 不断变大时就被后面的值超过了,即过时了。处理完过时决策后队首就是这一次的 \(g_i\) 。而入队维护单调性时,弹出队尾所有 \(tail\) 满足 \(f(tail)\ge f(x)\) ,因为 \(f(x)\) 显然越小越好,而 \(x\) 比它们大 \(f\) 的值还比它们小,显然可以直接取代。最终可以做到 \(\mathcal{O}(n)\) 求出 \(g_i\) 。求出来 \(g_i\) 之后这题才真正开始,统计答案需要高精度,各种卡空间卡时间,真是大毒瘤。总之最终时间复杂度 \(\mathcal{O}(n)\) ,足以通过本题。
#include <cstdio>
#include <cstring>
#define val(x) ((s[x] << 1) - s[g[x]])
typedef unsigned long long ull; const int base = 1e9;
const int mod = (1 << 30) - 1, N = 4e7 + 10, M = 1e5 + 10;
int g[N], b[N], p[M], q[N]; ull s[N];
template <typename T>
inline void read(T& x)
{
x = 0; char ch; int f = 1;
while ((ch = getchar()) < '0' || ch > '9')
f = (ch ^ '-' ? 1 : -1);
while (x = (x << 1) + (x << 3) + ch - '0',
(ch = getchar()) >= '0' && ch <= '9') ;
x *= f;
}
struct bigInt
{
int len; ull num[4];
bigInt() { len = 0; memset(num, 0, sizeof (num)); }
bigInt(ull x)
{ len = 0; while (x) num[len++] = x % base, x /= base; }
bigInt operator+(const bigInt& x)
{
bigInt res;
res.len = len > x.len ? len : x.len; ull k = 0;
for (int i = 0; i < res.len; ++i)
{
res.num[i] = num[i] + x.num[i] + k;
k = res.num[i] / base; res.num[i] -= base * k;
}
while (k) { res.num[res.len++] = k % base; k /= base; }
return res;
}
bigInt operator*(const bigInt& x)
{
bigInt res;
res.len = len + x.len - 1; ull k = 0;
for (int i = 0; i < len; ++i)
for (int j = 0; j < x.len; ++j)
res.num[i + j] += num[i] * x.num[j];
for (int i = 0; i < res.len; ++i)
{
res.num[i] += k;
k = res.num[i] / base;
res.num[i] -= base * k;
}
while (k) { res.num[res.len++] = k % base; k /= base; }
return res;
}
}ans;
inline void print(const bigInt& x)
{
printf("%llu", x.num[x.len - 1]);
for (int i = x.len - 2; ~i; --i) printf("%llu", x.num[i]);
}
int main()
{
int n, type; read(n); read(type);
if (type)
{
ull x, y; int z, m, l, r;
read(x); read(y); read(z); read(b[1]); read(b[2]); read(m);
for (int i = 3; i <= n; ++i)
b[i] = (x * b[i - 1] & mod) + (y * b[i - 2] & mod) + z & mod;
for (int j = 1; j <= m; ++j)
{
read(p[j]); read(l); read(r);
for (int i = p[j - 1] + 1, a; i <= p[j]; s[i] = s[i - 1] + a, ++i)
a = b[i] % (r - l + 1) + l;
}
}
else for (int i = 1, a; i <= n; s[i] = s[i - 1] + a, ++i) read(a);
int head = 1, tail = 1;
for (int i = 1; i <= n; ++i)
{
while (head < tail && val(q[head + 1]) <= s[i]) ++head;
g[i] = q[head];
while (head <= tail && val(q[tail]) >= val(i)) --tail;
q[++tail] = i;
}
for (int pos = n; pos; pos = g[pos])
{
bigInt tmp(s[pos] - s[g[pos]]);
ans = ans + tmp * tmp;
}
print(ans); putchar('\n'); return 0;
}
[CSP-S2019] 树的重心
为什么这题评分会比 D1T3 低啊,不过有一说一我已经看不懂我之前在写什么了。
给出一个有 \(n\) 个结点的树 \(\mathcal{T}\),求出 \(\mathcal{T}\) 单独去掉每条边后分裂出来的两棵子树重心编号之和,即
(\(1\le n\le 3\times10^5\))
一道非常神仙的二次扫描换根 \(\rm dp\) 。首先我们要知道重心的一种求法:
如果我们现在在 \(x\) ,判断 \(x\) 是否是重心,如果是,则找到重心算法结束,否则进入 \(x\) 的重儿子递归搜索。
类似倍增求 \(\rm lca\) ,我们第一遍 \(\rm dfs\) 考虑构造一个重儿子链,每次倍增往下跳,这样可以做到对于一个结点 \(\mathcal{O}(\log n)\) 的时间求重心。而这样只能找到一个重心,但一棵树可能有两个重心。不过没关系,我们只需要找到一个重心后判一下它的重儿子和父亲是不是重心就行了,因为另外一个重心显然只可能是这俩的其中一个。现在对于指定子树找重心的问题解决了,接下来我们解决删边的问题。
删去一条边 \((u,v)\) 得到的两棵子树有两个部分:子树内和子树外。我们令 \(v\) 对应的是子树内,\(u\) 对应的是子树外,如图,绿色对应的是子树内,红色对应的是子树外:
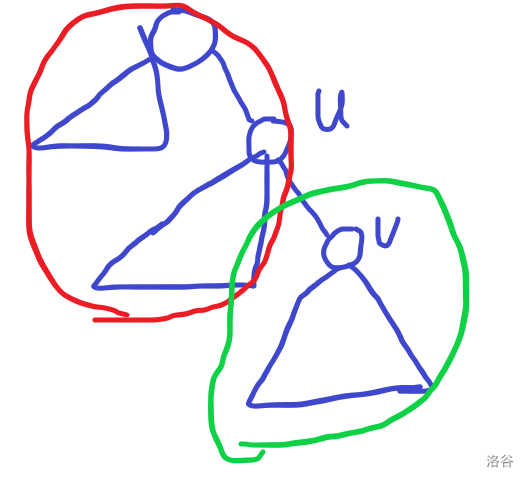
对于子树内的部分很好处理,我们按照之前维护出来的以 \(1\) 为根的重儿子链跳就好了,但对于子树外的就不太好处理了。因为它的重儿子链有一点变化,但不是很大,只有 \(u\) 的重儿子有所变化,但跳到 \(u\) 的重儿子后就一切跟 \(1\) 为根时一样了。所以这启示我们找到 \(u\) 为根时的重儿子,之后暴力更新 \(u\) 对应的重儿子链。具体来讲,在第二次 \(\rm dfs\) 换根的过程中,对于 \((u,v)\) 这条边,我们把 \(u,v\) 为根时它们对应的 \(size,fa,son\) 更新一下,然后更新重儿子链,接着跳重儿子链找重心,接着把根换到 \(v\) 递归下去,最后在退出 \(u\) 时,回溯一下结点信息就好。
最后一个问题,怎么找到 \(u\) 的重儿子。显然,\(u\) 为根时,作比较的应该是 \(u\) 原本的重儿子和它父亲结点在以 \(u\) 为根时对应的 \(size\) 。但非常遗憾,如果 \(v\) 对应的就是 \(u\) 的重儿子,它被删掉之后这个比较就是有问题的。所以我们还要额外维护一个次重儿子。当在换根的过程中重儿子被删掉时就用它作比较。这样这道题就做完了,一些实现细节可以详见代码,时间复杂度 \(\mathcal{O}(n\log n)\) 。
#include <cstdio>
#include <cstring>
inline int max(const int& a1, const int& a2) { return a1 > a2 ? a1 : a2; }
inline void swap(int& a1, int& a2) { int t = a1; a1 = a2; a2 = t; }
const int N = 3e5 + 10;
struct edge{ int v, next, u; }E[N << 1]; int p[N], cnt;
inline void init() { memset(p, -1, sizeof p); cnt = 0; }
inline void insert(int u, int v) { E[cnt].u = u; E[cnt].v = v; E[cnt].next = p[u]; p[u] = cnt++; }
//ff,ssize,sson 是在换根之后对应更新的信息
int size[N], son[N], mson[N], pi[N][40], fa[N], sson[N], ssize[N], ff[N]; long long ans;
void dfs1(int u, int f)
{
size[u] = 1; fa[u] = f;
for (int i = p[u], v; i + 1; i = E[i].next)
{
v = E[i].v; if (v == f) continue;
dfs1(v, u); size[u] += size[v];
if (size[v] > size[son[u]]) mson[u] = son[u], son[u] = v;
else if (size[v] > size[mson[u]]) mson[u] = v;
}
pi[u][0] = son[u];
for (int i = 1; i <= 35; i++) pi[u][i] = pi[pi[u][i - 1]][i - 1];
}
//判断是否是重心
inline int judge(int u, int sum) { return u * (max(ssize[sson[u]], sum - ssize[u]) <= sum / 2); }
void dfs2(int u, int f)
{
for (int i = p[u], v, b; i + 1; i = E[i].next)
{
v = E[i].v; if (v == f) continue;
ssize[u] = size[1] - size[v]; ff[u] = ff[v] = 0;
if (son[u] == v) sson[u] = mson[u];
else sson[u] = son[u];
if (ssize[f] > ssize[sson[u]]) sson[u] = f;
pi[u][0] = sson[u];
for (int j = 1; j <= 35; j++) pi[u][j] = pi[pi[u][j - 1]][j - 1];
//跳重儿子链类似倍增lca
b = u; for (int j = 35; j >= 0; j--) if (ssize[u] - ssize[pi[b][j]] <= ssize[u] / 2) b = pi[b][j];
ans += judge(sson[b], ssize[u]) + judge(b, ssize[u]) + judge(ff[b], ssize[u]);
b = v; for (int j = 35; j >= 0; j--) if (ssize[v] - ssize[pi[b][j]] <= ssize[v] / 2) b = pi[b][j];
ans += judge(sson[b], ssize[v]) + judge(b, ssize[v]) + judge(ff[b], ssize[v]);
ff[u] = v; dfs2(v, u);
}
sson[u] = pi[u][0] = son[u]; ff[u] = fa[u];
for (int i = 1; i <= 35; i++) pi[u][i] = pi[pi[u][i - 1]][i - 1];
ssize[u] = size[u];
}
int main()
{
int T, n, x, y; scanf("%d", &T);
while (T--)
{
init(); memset(son, 0, sizeof son); memset(ff, 0, sizeof ff); memset(fa, 0, sizeof fa);
scanf("%d", &n);
for (int i = 1; i < n; i++) scanf("%d%d", &x, &y), insert(x, y), insert(y, x);
dfs1(1, 0);
for (int i = 1; i <= n; i++) ssize[i] = size[i];
for (int i = 1; i <= n; i++) sson[i] = son[i];
for (int i = 1; i <= n; i++) ff[i] = fa[i];
dfs2(1, 0);
printf("%lld\n", ans); ans = 0;
}
return 0;
}
总结
- 在面对类似格雷码这样不算太难的题目,出题人一般会挖个小坑卡掉一些人,一定要注意这些小坑,比如格雷码的
1ull << n。 - 括号树这种子树差分的思想很常用,一个点子树内的贡献等于进入子树前整体的贡献和进入子树后递归回来回溯时的贡献之差。
- 面对一道感觉有点奇妙性质但无从下手的题目,类似树上的数时,可以先从一些简单的部分分入手,逐个突破。
- 将不好直接计算的方案数补集转换,像 Emiya 家的饭一样,或者直接容斥甚至二反掉也是可以的,只是注意别一头盯着直接算钻死胡同。
- 面对数据范围比较离谱的题目,比如划分这道题时,一般都是推个 \(\rm dp\) 然后用各种 trick 加速,不过加速的前提是有 \(\rm dp\) 思路,所以要先思考一个成熟的 \(\rm dp\) 思想,再根据数据范围想优化。常见的 \(\mathcal{O}(n)\) 优化有单调队列,斜率优化等,\(\mathcal{O}(\log n)\) 的就矩阵快速幂,根据数据范围选择即可。
- 求重心的其中一种方法是跳重儿子链,一般在树的重心这种多次求解,且跟子树关系比较大的使用,依次删所有的边可以考虑二次扫描换根 \(\rm dp\) 。

