《算法》笔记 10 - 无向图
- 表示无向图的数据结构
- 邻接表数组
- 深度优先搜索
- 深度优先搜索寻找路径
- 深度优先搜索的性能特点
- 广度优先搜索
- 两种搜索方式的对比
图表示由相连的结点所表示的抽象模型，这个模型可以用来研究类似“能否从某个点到达指定的另一个点”、“有多少个结点和指定的结点相连”、“两个结点之间最短的连接是哪一条”。图的算法与很多实际问题相关。比如地图、搜索引擎、电路、任务调度、商业交易、计算机网络、社交网络等。
无向图是一种最简单、最基本的图模型，仅仅由一组顶点和一组能够将两个顶点相连的边组成。
在图的实现中，用从0开始的整数值来表示图的结点，用类似8-5来表示连接结点8和5的边，在无向图中，这与5-8表示的是同一条边。4-6-3-9表示的是4到9之间的一条路径。
表示无向图的数据结构
无向图的API
public class Graph{
Graph(int V) //创建一个含有V个顶点但不含有边的图
Graph(In in) //从标准输入流in读入一幅图
int v() //顶点数
int E() //边数
void addEdge(int v， int w) //向图中添加一条边v-w
Iterable<Integer>adj(intv) //和相邻的所有顶点
String toString() //对象的字符串表示
}
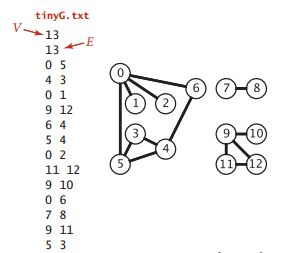
第二个构造函数接受的输入由2*E+2个整数组成，前两行分别是V和E，表示图中顶点和边的数量。接下来每行都是一对互相连接的顶点。
邻接表数组
可以选择邻接表数组作为实现Graph的数据结构，它将每个顶点的所有相邻顶点都保存在一张链表中，读取tingG后构造的邻接表数组如图所示：
代码实现：
public class Graph {
private final int V; // vertex
private int E; // edge
private Bag<Integer>[] adj;
public Graph(int V) {
this.V = V;
this.E = 0;
adj = (Bag<Integer>[]) new Bag[V];
for (int v = 0; v < V; v++) {
adj[v] = new Bag<Integer>();
}
}
public Graph(In in) {
this(in.readInt());
int E = in.readInt();
for (int i = 0; i < E; i++) {
int v = in.readInt();
int w = in.readInt();
addEdge(v, w);
}
}
public int V() {
return V;
}
public int E() {
return E;
}
public void addEdge(int v, int w) {
adj[v].add(w);
adj[w].add(v);
E++;
}
public Iterable<Integer> adj(int v) {
return adj[v];
}
}
用数组adj[]来表示图的顶点，可以快速访问给定顶点的邻接顶点列表；用Bag数据类型来存储一个顶点的所有邻接顶点，可以保证在常数时间内添加新的边或者遍历任意顶点的邻接顶点。要添加比如5-8这条边时，addEdge方法除了会把8添加到5的邻接表中，还会把5添加到8的邻接表。
这种实现的性能特点为:
- 使用的空间和V+E成正比
- 添加一条边所需的时间为常数
- 遍历顶点一个顶点的相邻顶点所需的时间和这个顶点的度数成正比（顶点的度数表示与这个顶点相连的边数）
深度优先搜索
深度优先搜索是一种遍历图的方式，这种算法的轨迹与走迷宫非常类似。可以将迷宫作为图，迷宫的通道作为图的边，迷宫的路口作为图的点，迷宫可认为是一种直观的图。探索迷宫的一种方法叫做Tremaux搜索。这种方法的具体做法是，选择一条没有标记过的通道，在走过的路上铺一条绳子；标记所有第一次经过的路口和通道；当来到第一个标记过的路口时，回退到上一个路口；当回退的路口已没有可走的通道时继续回退。
这样，最终可以找到一条出路，而且不会多次经过同一通道或者路口。
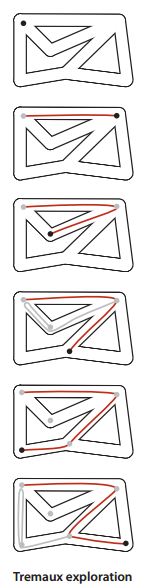
深度优先搜索的代码实现与走迷宫类似：
public class DepthFirstSearch {
private boolean[] marked;
private int count;
private final int s;
public DepthFirstSearch(Graph G, int s) {
marked = new boolean[G.V()];
this.s = s;
dfs(G, s);
}
private void dfs(Graph G, int v) {
marked[v] = true;
for (int w : G.adj(v)) {
if (!marked[w]) {
dfs(G, w);
}
}
}
public boolean marked(int w) {
return marked[w];
}
public int count() {
return count;
}
}
这段代码会搜索出所有与顶点s相邻的点，中dfs()方法的递归调用机制以及marked数组对应迷宫中的绳子的作用，当已经处理完一个顶点的所有相邻顶点后，递归会结束。算法在运行的时候，总是会沿着一个顶点的第一个相邻顶点不断深入，直到遇到一个在marked数组已经标记的顶点，才逐层退出递归，这也是深度优先搜索名称的由来。最终搜索的结果存储在marked数组中，标记为true的位对应的索引就是与顶点s相连的点。
深度优先搜索寻找路径
深度优先搜索可以解决路径检测问题，即回答“两个给定的顶点之间是否存在一条路径？”，但如果想找出这条路径呢？要回答这个问题，只需要对上面的代码稍作扩展：
public class DepthFirstPaths {
private boolean[] marked;
private int[] edgeTo; //新增的，用于记录路径
private final int s;
public DepthFirstPaths(Graph G, int s) {
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
this.s = s;
dfs(G, s);
}
private void dfs(Graph G, int v) {
marked[v] = true;
for (int w : G.adj(v)) {
if (!marked[w]) {
edgeTo[w] = v; //记录路径
dfs(G, w);
}
}
}
public boolean marked(int w) {
return marked[w];
}
public int count() {
return count;
}
public boolean hasPathTo(int v) { //判断是否存在从s到v的路径
return marked(v);
}
public Iterable<Integer> pathTo(int v) { //获取从s到v的路径，不存在则返回null
if (!hasPathTo(v))
return null;
Stack<Integer> path = new Stack<Integer>();
for (int x = v; x != s; x = edgeTo[x]) {
path.push(x);
}
path.push(s);
return path;
}
public static void main(String[] args) {
In in = new In(args[0]);
Graph G = new Graph(in);
int s = Integer.parseInt(args[1]);
DepthFirstPaths search = new DepthFirstPaths(G, s);
//
for (int v = 0; v < G.V(); v++) {
StdOut.print(s+" to "+v+": ");
if(search.hasPathTo(v)){
for(int x:search.pathTo(v)){
if(x==s) StdOut.print(x);
else StdOut.print("-"+x);
}
}
StdOut.println();
}
}
}
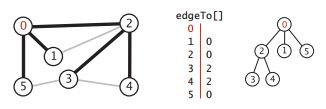
这段代码添加了edgeTo[]整形数组来起到Tremaux搜索中绳子的作用。每次由边v-w第一次访问w时，会将edgeTo[w]设为v，最终edgeTo数组是一颗以起点为根节点的树，记录了由任意连通的结点回到根节点的路径。
下图为由一副图生成的edgeTo的内容，及路径树的结构的示例：
这与代码运行结果是一致的：
java DepthFirstPaths tinyCG.txt 0
0 to 0：0
0 to 1：0-2-1
0 to 2：0-2
0 to 3：0-2-3
0 to 4：0-2-3-4
0 to 5：0-2-3-5
深度优先搜索的性能特点
深度优先搜索标记与起点连通的所有顶点所需的时间与顶点的度数之和成正比。
使用深度优先搜索得到从给定起点到任意标记顶点的路径所需的时间与路径的长度成正比。
广度优先搜索
深度优先搜索得到的路径不仅与图的结构有关，还受图的表示的影响，邻接表中顶点的顺序不同，得到的路径也会不同。所以当需要计算两点间的最短路径(单点最短路径)时，就无法依赖深度优先搜索了，而广度优先搜索可以解决单点最短路径问题。
要找到从s到v的最短路径，从s开始，在所有由一条边就可以到达的顶点中寻找v，如果找不到就继续在于s距离两条边的顶点中查找，如此一直进行。
public class BreadthFirstPaths {
private boolean[] marked;
private int[] edgeTo;
private final int s;
public BreadthFirstPaths(Graph G, int s) {
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
this.s = s;
bfs(G, s);
}
private void bfs(Graph G, int s) {
Queue<Integer> queue = new Queue<Integer>();
marked[s] = true;
queue.enqueue(s);
while (!queue.isEmpty()) {
int v = queue.dequeue();
for (int w : G.adj(v)) {
if(!marked[w]){
edgeTo[w]=v;
marked[w]=true;
queue.enqueue(w);
}
}
}
}
public boolean hasPathTo(int v){
return marked[v];
}
public Iterable<Integer> pathTo(int v) {
if (!hasPathTo(v))
return null;
Stack<Integer> path = new Stack<Integer>();
for (int a = v; a != s; a = edgeTo[a]) {
path.push(a);
}
path.push(s);
return path;
}
// cmd /c --% java algs4.four.BreadthFirstPaths ..\..\..\algs4-data\tinyCG.txt 0
public static void main(String[] args) {
In in = new In(args[0]);
int s = Integer.parseInt(args[1]);
Graph g = new Graph(in);
BreadthFirstPaths search = new BreadthFirstPaths(g, s);
for (int i = 0; i < g.V(); i++) {
StdOut.print(i + ":");
Iterable<Integer> path = search.pathTo(i);
for (Integer p : path) {
if (search.s != p) {
StdOut.print("-" + p);
} else {
StdOut.print(p);
}
}
StdOut.println();
}
}
}
方法bfs中定义了一个队列来保存所有已经被标记过但其邻接表还未被检查过的顶点。先将起点加入队列，然后重复以下步骤直到队列为空：
- 取队列中的下一个顶点v并标记它
- 将与v相邻的所有未被标记过的顶点加入队列。
队列先进先出(FIFO)的特性可以达到广度优先搜索寻找距离逐渐增大的效果。在深度优先搜索中，实际上隐式地使用了一个遵循后进先出(LIFO)规则的栈，在dfs的递归调用的过程中，这个栈由系统管理。
两种搜索方式的对比
不管是深度优先还是广度优先搜索算法，它们都会先将起点存入数据结构中，然后重复以下步骤直到数据结构被清空：
- 取其中的下一个顶点v并标记它
- 将与v相邻而又未被标记过的顶点加入数据结构中
两种算法的区别在于从数据结构中获取下一个顶点的规则，深度优先搜索会首先取最晚加入数据结构的顶点，而广度优先搜索取得则是最早加入的顶点。这种规则的区别会影响搜索图的路径，深度优先搜索会不断深入图中，并在栈中保存了所有分叉的顶点，广度优先搜索则像扇面一般扫描图，用一个队列保存访问过的最前段的顶点。
