《算法》笔记 4 - 归并排序

• 归并方法
• 自顶向下的归并排序
  • 实现
  • 性能分析
  • 优化：切换到插入排序
• 自底向上的归并排序

归并方法

“归并”操作是将两个有序的数组合并成一个更大的有序数组，归并排序就是基于这一操作，先递归地将一个数组分成两半分别排序，然后将排序结果归并起来。
归并的代码如下：

private static void merge(Comparable[] a, int lo, int mid, int hi) { 
    int i = lo, j = mid + 1;
    for (int k = lo; k <= hi; k++) {
        aux[k] = a[k];
    }

    for (int k = lo; k <= hi; k++) {
        if (i > mid) {
            a[k] = aux[j++];
        } else if (j > hi) {
            a[k] = aux[i++];
        } else if (less(aux[i], aux[j])) {
            a[k] = aux[i++];
        } else {
            a[k] = aux[j++];
        }
    }
}

这种归并方法用了一个辅助数组aux[]，在归并时，先将待归并的元素复制到辅助数组，然后将子数组a[lo..mid]和a[mid+1..hi]归并成一个有序的数组，同时将数组归并回a[]。i，j分别指向左右两个子数组的待归并元素，执行时如果左半边数组用尽，则取右半边元素，右指针加1，如果右半边数组用尽，则取左半边元素，左指针加1，如果两边数组都没用尽，则通过指针各取一个元素比较大小，将小的元素归并回原数组，同时对应的指针加1。
这个归并方法能够将两个子数组排序，然后就可以通过它将整个数组排序。

归并排序的代码实现有自顶向下和自底向上两种。

自顶向下的归并排序

实现

public class Merge {
	private static Comparable[] aux;

    private static void sort(Comparable[] a, int lo, int hi) {
        if (hi <= lo) {
            return;
        }
        int mid = lo + (hi - lo) / 2;
        sort(a, lo, mid);
        sort(a, mid + 1, hi);
        merge(a, lo, mid, hi);
    }

    public static void sort(Comparable[] a) {
        aux = new Comparable[a.length];
        sort(a, 0, a.length - 1);
    }
}

其中aux为归并所需的辅助数组，在排序开始前初始化。sort(Comparable[] a, int lo, int hi)方法递归地调用自己，将一个大的数组不断地分为左右两部分，并最终进行归并。将一个长度16的数组排序的轨迹如下图：

要将a[0..15]排序， sortO方法会调用自己将a[0..7]排序，再在其中调用自己将a[0..3]和a[0..1]排序。在将a[0]和a[1]分别排序之后，终于才会开始将a[0]和a[1]归并。第二次归并是a[2]和a[3]，然后是a[0..1]和a[2..3]，以此类推。从这段轨迹可以看到， sort()方法的作用其实在于安排多次merge()方法调用的正确顺序。
所以这种方式在不断地将数组分割然后排序，所以也称自顶向下的归并。

性能分析

关系归并排序算法的性能，还是从比较和访问数组的次数来分析。
下面的树状图直观地表示了归并排序的执行过程，每个结点都表示一个sort()方法通过merge()方法归并而成的子数组。对于长度为N的数组，这颗二叉树的高度为lgN，在经过层层归并的过程中，每一层都最多需要N次比较，比如将a[0..7]和a[8..15]归并为a[0..15]时，16个元素都会经过一次比较被放回原数组，然后再往下层走，不管需要几次归并，处理的元素都是16个，既16次比较。每层N次比较，则一共NlgN次比较。

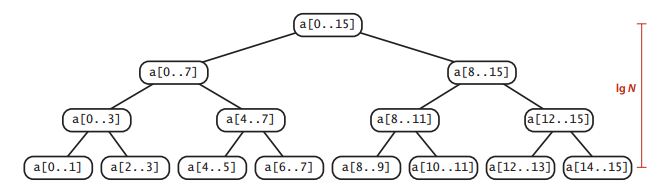
所以归并排序的增长数量级为NlgN级别的，这相比之前的选择、插入排序的平方级别，要快太多了。

将1万条随机整数进行排序时，插入排序与归并排序的速度对比如下：

Insertion, 0.868 s
Merge, 0.018 s

优化：切换到插入排序

上面的归并排序代码还可以继续优化，优化的方式之一便是在小规模数组时，切换到插入排序。因为当递归分割到最下面几层的子数组时，子数组的规模已经非常小了，继续递归只会使方法的调用过于频繁。用不同的方法处理小规模问题能改进大多数递归算法的性能，在小规模问题上，插入排序或者选择排序可能比归并排序更快，而且这样做可以有效减少递归的深度，减少方法调用的开销。

public class MergeOptimize {
    private static int CUTOFF = 20;

    private static void sort(Comparable[] src, Comparable[] dst, int lo, int hi) {
        if (hi <= lo + CUTOFF) {
            insertionSort(dst, lo, hi);
            return;
        }

        int mid = lo + (hi - lo) / 2;
        sort(src, dst, lo, mid);
        sort(src, dst, mid + 1, hi);
        merge(src, dst, lo, mid, hi);
    }
    ...
}

在数组规模小于20的时候，改用插入排序。
用10万条随机整数来检验优化后的效果：

Merge, 0.305 s
MergeOptimize, 0.199 s

自底向上的归并排序

自底向上的归并排序区别于自顶向上排序方法的地方在于，后者将一个大问题分割成小问题分别解决，然后用所有小问题的答案来解决整个大问题，属于分治思想的典型应用；而自底向上的归并排序则是直接从最小规模的数组开始归并，不断得到规模更大的数组，最终得以将整个数组排序。比如依次进行1-1,2-2,4-4归并，子数组的大小不断翻倍。

public class MergeBU {

    private static Comparable[] aux;
    public static void sort(Comparable[] a) {
        int N = a.length;
        aux = new Comparable[N];
        for (int sz = 1; sz < N; sz = sz + sz) {
            for (int lo = 0; lo < N - sz; lo += sz + sz) {
                merge(a, lo, lo + sz - 1, Math.min(lo + sz + sz - 1, N - 1));
            }
        }
    }
    ...
}

自底向上的归并排序的增长数量级仍然是NlgN级别的，因为其原理仍然是基于归并的。在实际运行时，可能由于少了函数递归调用的开销，比自顶向下的归并排序还能更快，如下为10万条随机整数的测试结果：

Merge, 0.279
MergeBU, 0.172