二进制的详细展开
1.二进制转换成十进制
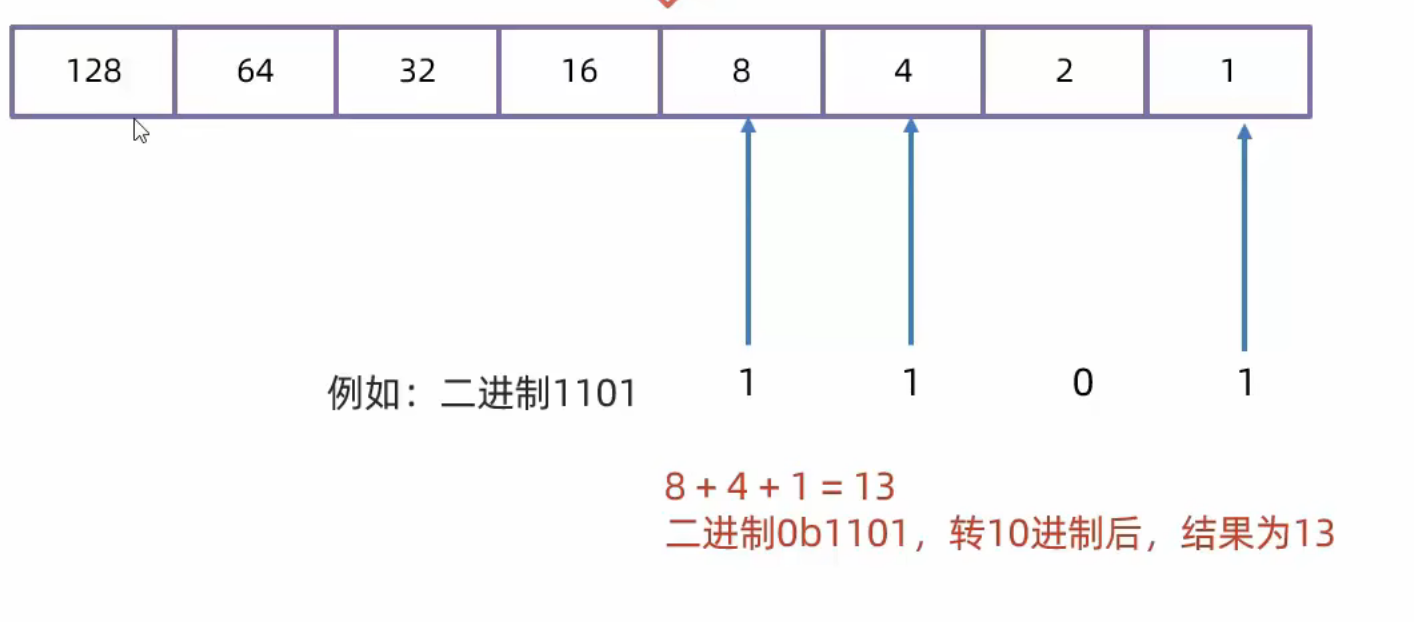
使用8421快速转换法
使用方法:
1.从右往左写出8421表格(就是每个数字都*2)
2.二进制数从右往左依次对应8421表格
3.二进制的数中,0不取,1取
4.将取出来的数进行相加即可
2.二进制的原码、反码、补码
1.原码:是数据的二进制体现形式,一个字节由8个二进制位组成
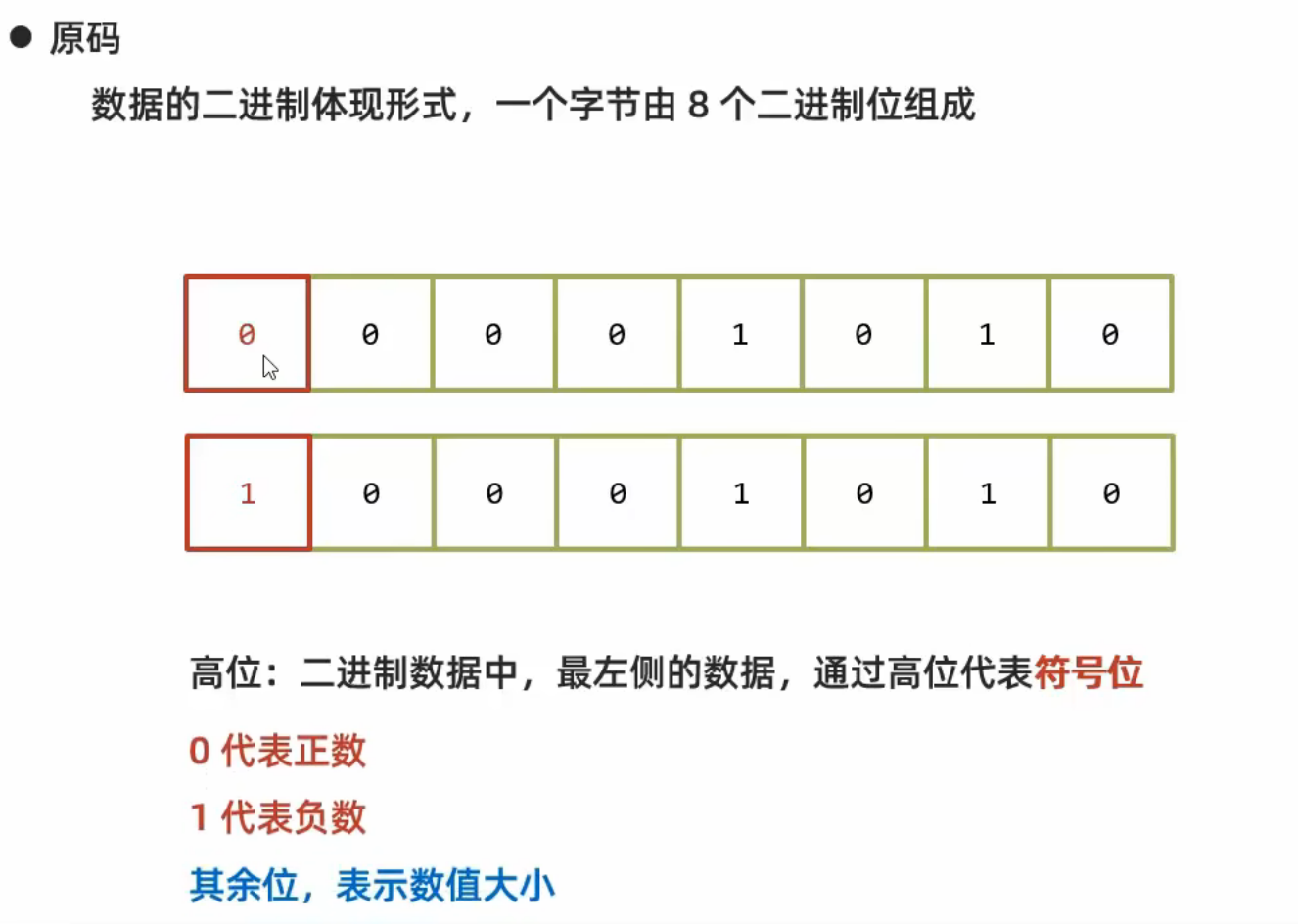
高位即二进制数开头第一位,表示符号位,高位为0则为正数,为1则为负数。其余位表示数值大小
引出:在上面的附图中,两个二进制位在十进制中分别表示10和-10,按照道理来说相加应该是0,但实际算出却是-20
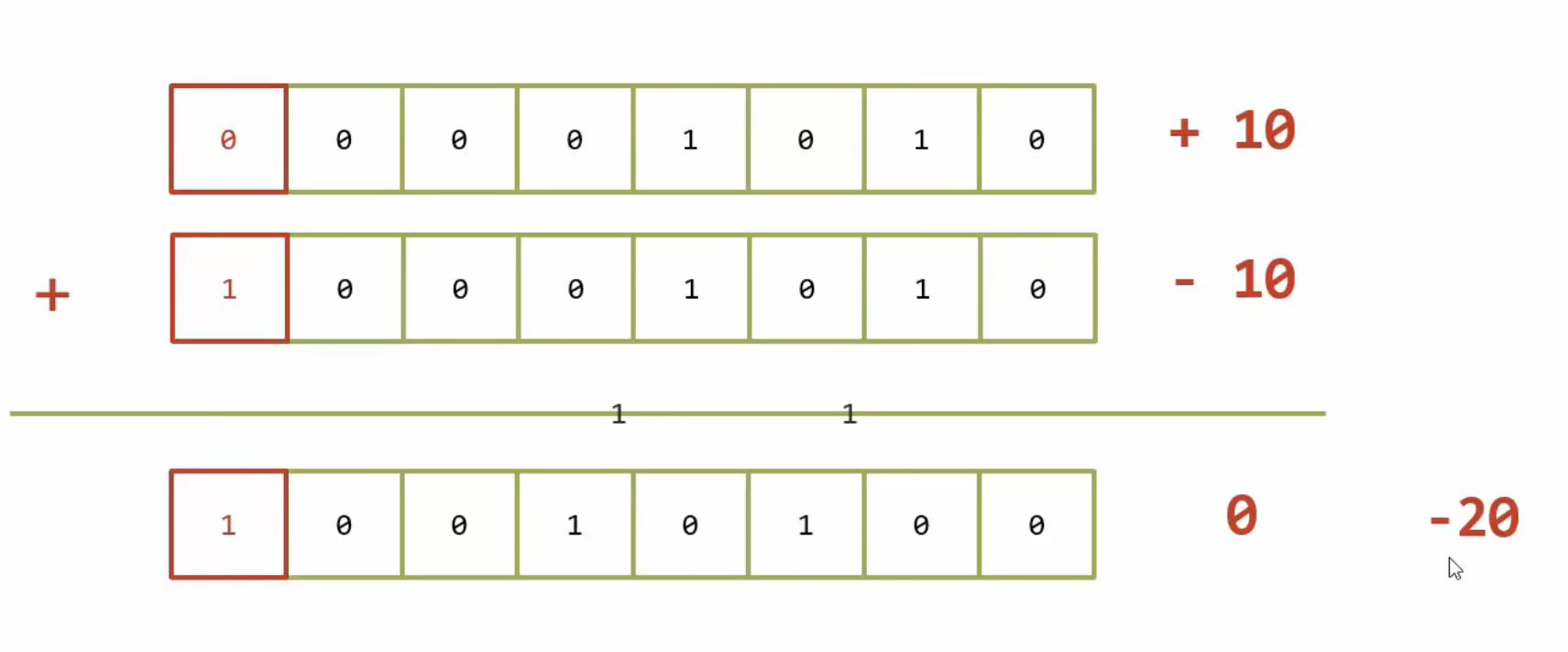
从右开始算,0+0还是0,1+1逢2向前进1,0+1 写1 1+1逢2再进1...
由此得出结论,二进制原码的弊端是遇到负数运算会出现错误
知识: 计算机在运算的时候都是以二进制补码的形式在运算
2.反码
- 正数的反码与其原码相同
- 负数的反码是对原码逐位取反,但符号位除外
3.补码
- 正数的补码与其原码相同
- 负数的补码是在其反码的末位加1
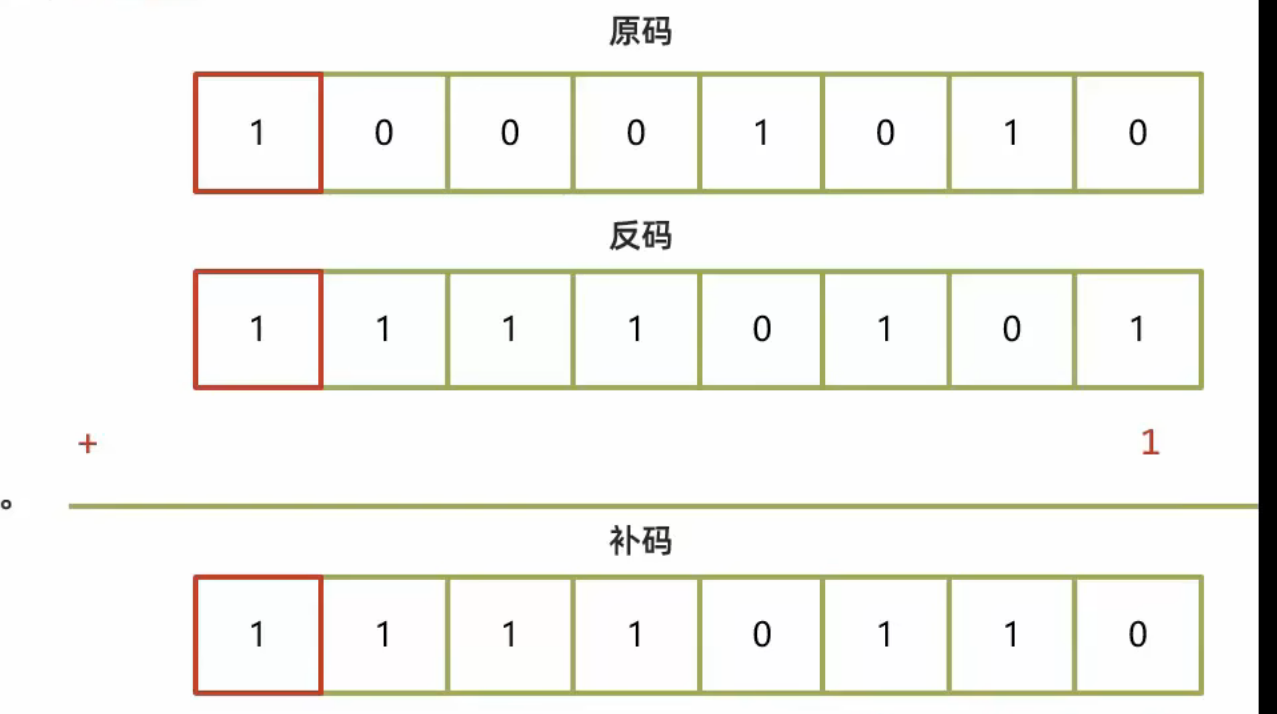
解答:接着我们用10的补码和-10的补码进行运算
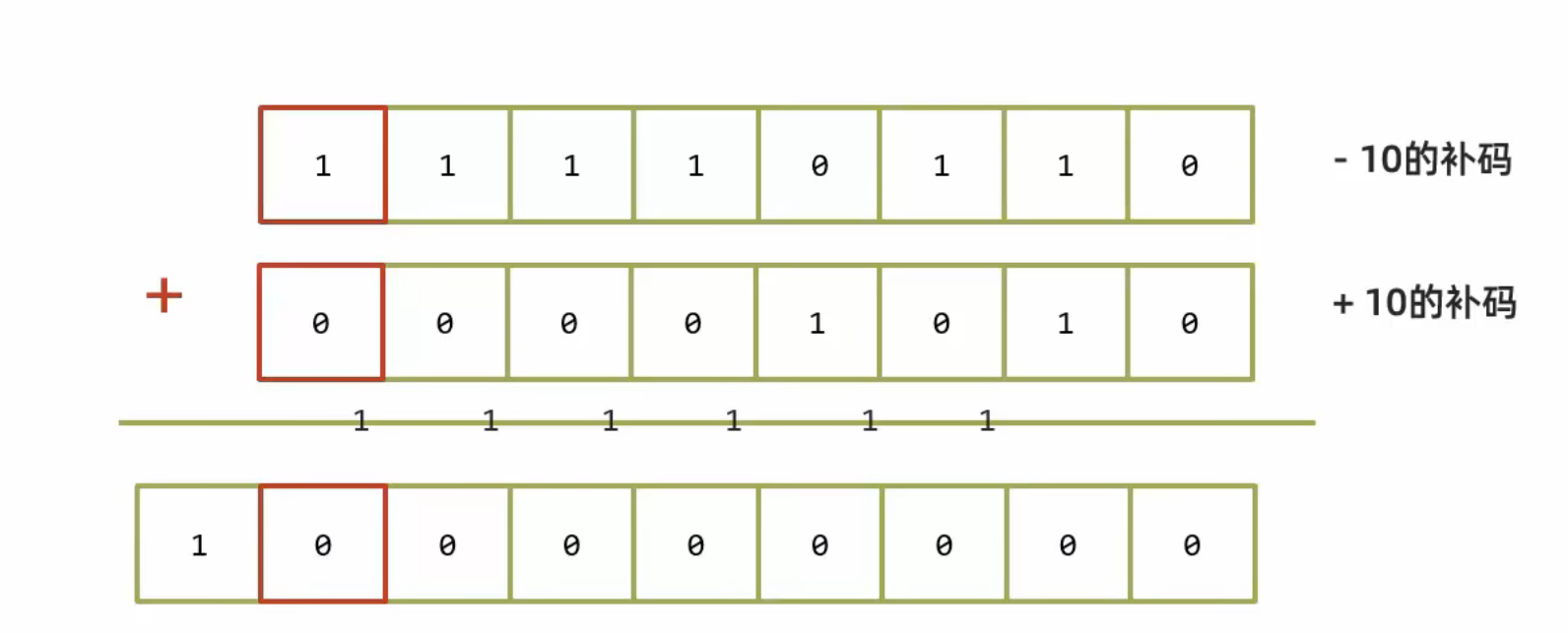
1个字节由8个二进制位组成,所以开头的1舍去,最后得到就是0
3.解答强转中的精度损失问题
之前我们设定的130在经过强转后得出的结果是-126
解答:首先知道130的二进制位是1000 0010 又因为是int类型,占4个字节,所以要在前面补上3个字节。
.
强转到byte后占1个字节,会强行砍掉前面3个字节直接得到1000 0010,这时我们会发现二进制位变成负数了
.
又因为运算的时候是补码,所以我们还要反推出原码(还是一样的步骤,先取反,再加1)最后得出原码是1111 1110 也就是-126
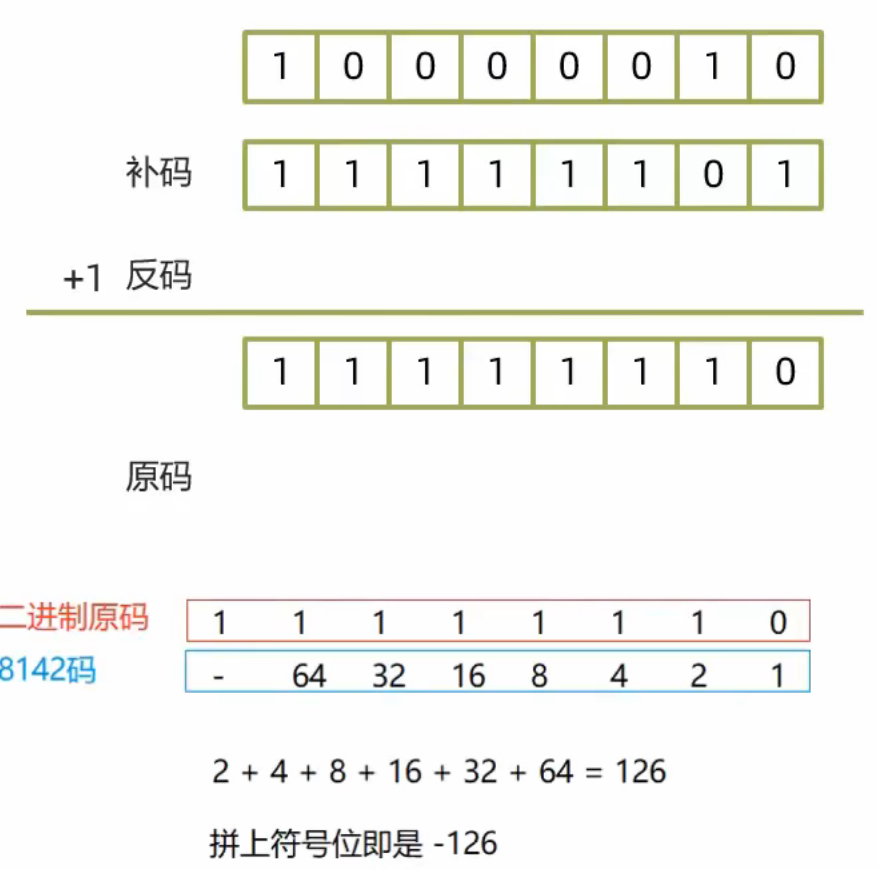
(附图中第一个是补码,以此类推)



