矩阵范数和矩阵求导

今天发现两篇宝藏文章，关于矩阵范数和矩阵求导的，转载收藏一下。感谢大佬们的分享！{抱拳}
矩阵范数 转载自：https://blog.csdn.net/sylar49/article/details/77510160

今天看了半天强化学习，看得很不开心。。。因为一直处于懵圈状态。。。
于是乎不想看了，稍微总结一下矩阵范数的求解来放松一下身心吧~

这里总结的矩阵范数主要是F范数、1范数、2范数、核范数以及全变分TV范数与1、2的搭配

1、F范数

概念：

∥X∥F=∑i=1m∑j=1nx2ij−−−−−−−−⎷$$\Vert X{\Vert }_F=\sqrt{\sum _{i=1}^m\sum _{j=1}^n{x}_{ij}^2}$$

矩阵各个元素平方和开根，概念上非常像向量的L2范数
导数：求导的方法则是将其展开来，一般情况下我们不会直接求原始的范数||A||F，因为很麻烦，即使是在损失函数中也是用F范数的平方项来简化运算，而常见的损失函数一般是

12||Y−X||2F$$\frac{1}{2}||Y-X|{|}_F^2$$

，此时对X求导，则需要将内部的Y-X展开来
（Y−X）T∗（Y−X）=YTY+2∗XTY+XTX$（Y-X{）}^T\ast （Y-X）=Y^{T}Y+2\ast X^{T}Y+X^{T}X$，所以对 12||Y−X||2F$\frac{1}{2}||Y-X|{|}_F^2$中X求导即为 X−Y$X-Y$

2、1范数

概念：║A║1 = max{ ∑|ai1|, ∑|ai2| ,…… ,∑|ain| } (列和范数，A每一列元素绝对值之和的最大值)　(其中∑|ai1|第一列元素绝对值的和∑|ai1|=|a11|+|a21|+…+|an1|,其余类似)；
矩阵的1范数和向量的1范数雷同，不能直接求解，只能分情况讨论
求导：常规的L1范数的求导是在损失函数中作为正则项出现，即12||Y−X||2F+λ1||X||1$\frac{1}{2}||Y-X|{|}_F^2+{\lambda }_1||X|{|}_1$，这里前半部分求导是X−Y$X-Y$，后半部分则需要分情况讨论，最终结果为为

[Sλ(Y)]i=⎧⎩⎨yi−λ0yi+λifyi>λif−λ≤yi≤λifyi<−λ$$[{\mathcal{S}}_{\lambda }(Y){]}_i=\{\begin{array}{rl}{y}_i-\lambda & \text{if}{y}_i>\lambda \\ 0& \text{if}-\lambda \le y_i\le \lambda \\ y_i+\lambda & \text{if}{y}_i<-\lambda \end{array}$$

3、2范数

概念：||A||2$||A|{|}_2$指的是A最大的奇异值或者半正定矩阵A*A最大特征值开根
求导：对于问题argminX12∥X−V∥2F+λ∥X∥2$\arg \underset{X}{min}\frac{1}{2}\Vert X-V{\Vert }_F^2+\lambda \Vert X{\Vert }_2$存在近似解|V|2−λ|V|2V$\frac{|V{|}_2-\lambda }{|V{|}_2}V$

4、TV范数

概念：全变分范数，其实就是对矩阵乘上一个一阶的差分矩阵，乘完还是个矩阵，所以要一般要结合前边的1范数或者2范数再对其进行约束求解

5、核范数

概念：即矩阵奇异值的和
求解：对于minX112∥Y−X1∥2F+λ1∥X1∥⋆$\underset{X_1}{min}\frac{1}{2}\Vert Y-X_1{\Vert }_F^2+{\lambda }_1\Vert X_1{\Vert }_{\star }$
存在近似解X1^=Dλ1(Y)$\widehat{X_1}={\mathcal{D}}_{{\lambda }_1}(Y)$
Dλ${\mathcal{D}}_{\lambda }$ 表示∑i=1r(σi−λ)+uivTi$\sum _{i=1}^r({\sigma }_i-\lambda {)}_{+}{u}_i{v}_i^T$

这里, (x)+=max(0,x)$(x{)}_{+}=max(0,x)$. ui$u_i$, vi$v_i$ 和 σi${\sigma }_i$ 分别是<script type="math/tex" id="MathJax-Element-1851">M</script>的左奇异向量、右奇异向量和奇异值

（markdown模式下可以用latex写东西真的太方便了= =

至于各个范数的效果，实质上1范数和2范数在矩阵分解上效果差得不多，基本上2范数能分离出的高频成分1范数能更快的分离出来，在一维层面上也容易想想，1范数相比2范数能够更快的收敛（直指坐标中心），核范数效果对低频成分的提取也比TV_1/TV_2范数的效果要好很多。

具体的实现可以关注一下我师弟在这个月投在BIBM上一个关于矩阵范数的toolbox论文。应该很快就可以出结果了。o(￣▽￣)ブ

参考文献
Cai J F, Candès E J, Shen Z. A Singular Value Thresholding Algorithm for Matrix Completion[J]. Siam Journal on Optimization, 2010, 20(4):1956-1982.
矩阵的 Frobenius 范数及其求偏导法则 http://blog.csdn.net/txwh0820/article/details/46392293

矩阵求导 转载自：https://blog.csdn.net/txwh0820/article/details/46392293

矩阵的迹求导法则

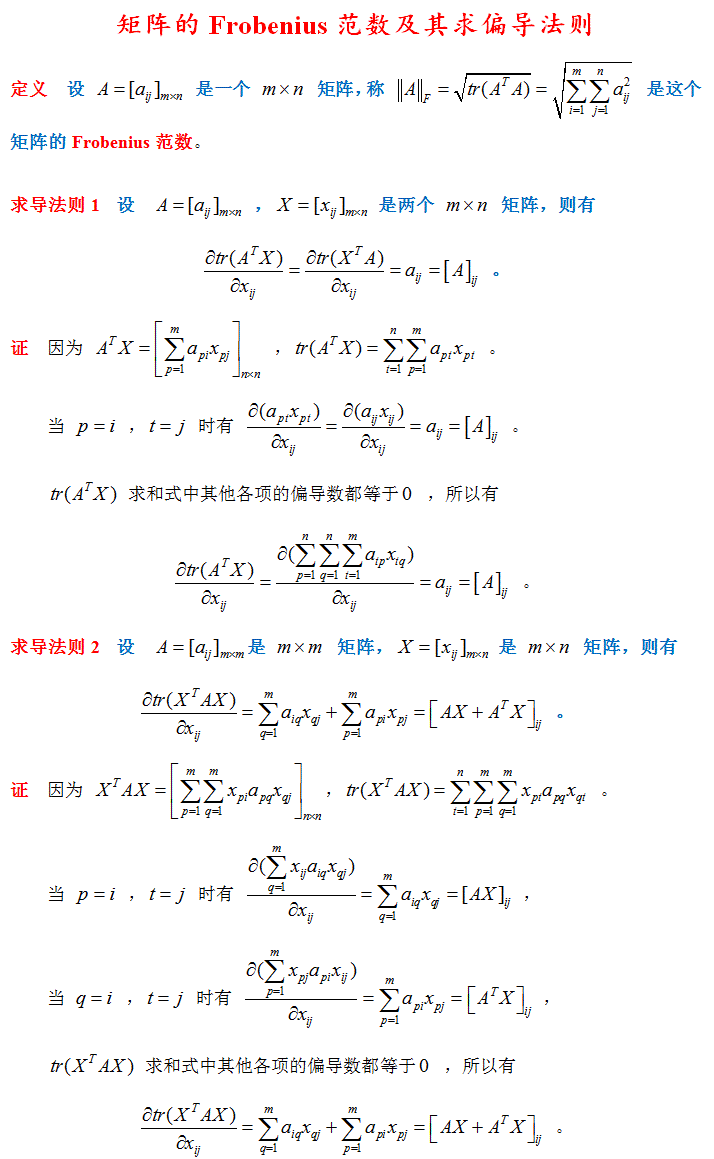
1. 复杂矩阵问题求导方法：可以从小到大，从scalar到vector再到matrix


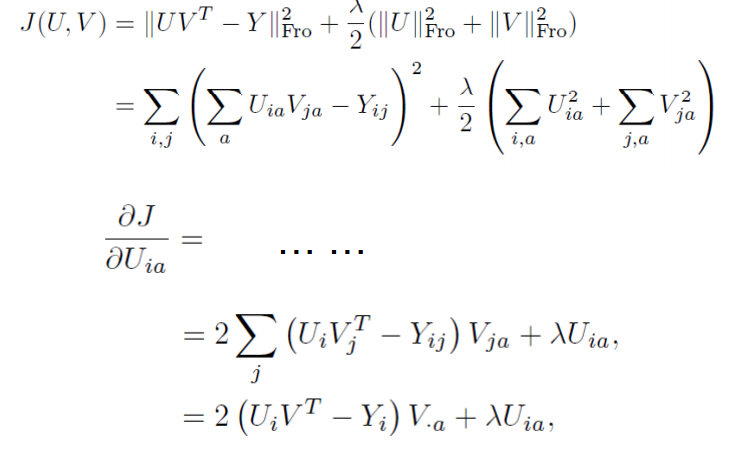
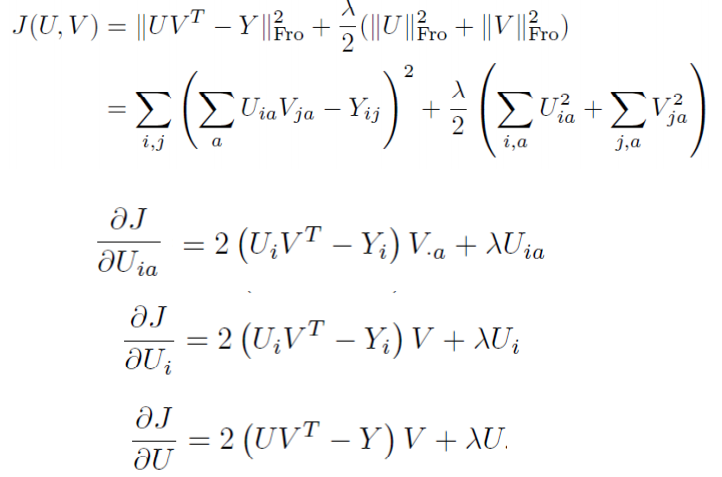
2. x is a column vector, A is a matrix

d(A∗x)/dx=A$d(A\ast x)/dx=A$
d(xT∗A)/dxT=A$d(x^T\ast A)/d{x}^T=A$
d(xT∗A)/dx=AT$d(x^T\ast A)/dx=A^T$
d(xT∗A∗x)/dx=xT(AT+A)$d(x^T\ast A\ast x)/dx=x^T(A^T+A)$

3. Practice:

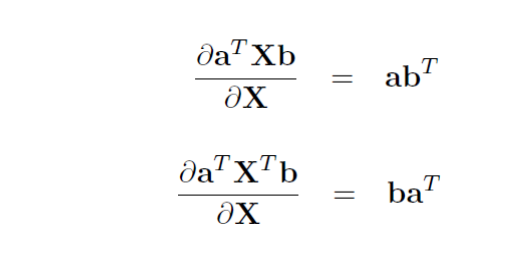
4. 矩阵求导计算法则
求导公式(撇号为转置）：
Y = A * X –> DY/DX = A’
Y = X * A –> DY/DX = A
Y = A’ * X * B –> DY/DX = A * B’
Y = A’ * X’ * B –> DY/DX = B * A’
乘积的导数：
d(f*g)/dx=(df’/dx)g+(dg/dx)f’

一些结论：

1. 矩阵Y对标量x求导：
   相当于每个元素求导数后转置一下，注意M×N矩阵求导后变成N×M了
   Y = [y(ij)]–> dY/dx = [dy(ji)/dx]
2. 标量y对列向量X求导：
   注意与上面不同，这次括号内是求偏导，不转置，对N×1向量求导后还是N×1向量
   y = f(x1,x2,..,xn) –> dy/dX= (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)’
3. 行向量Y’对列向量X求导：
   注意1×M向量对N×1向量求导后是N×M矩阵。
   将Y的每一列对X求偏导，将各列构成一个矩阵。
   重要结论：
   dX’/dX =I
   d(AX)’/dX =A’
4. 列向量Y对行向量X’求导：
   转化为行向量Y’对列向量X的导数，然后转置。
   注意M×1向量对1×N向量求导结果为M×N矩阵。
   dY/dX’ =(dY’/dX)’
5. 向量积对列向量X求导运算法则：
   注意与标量求导有点不同。
   d(UV’)/dX =(dU/dX)V’ + U(dV’/dX)
   d(U’V)/dX =(dU’/dX)V + (dV’/dX)U’
   重要结论：
   d(X’A)/dX =(dX’/dX)A + (dA/dX)X’ = IA + 0X’ = A
   d(AX)/dX’ =(d(X’A’)/dX)’ = (A’)’ = A
   d(X’AX)/dX =(dX’/dX)AX + (d(AX)’/dX)X = AX + A’X
6. 矩阵Y对列向量X求导：
   将Y对X的每一个分量求偏导，构成一个超向量。
   注意该向量的每一个元素都是一个矩阵。
7. 矩阵积对列向量求导法则：
   d(uV)/dX =(du/dX)V + u(dV/dX)
   d(UV)/dX =(dU/dX)V + U(dV/dX)
   重要结论：
   d(X’A)/dX =(dX’/dX)A + X’(dA/dX) = IA + X’0 = A
8. 标量y对矩阵X的导数：
   类似标量y对列向量X的导数，
   把y对每个X的元素求偏导，不用转置。
   dy/dX = [Dy/Dx(ij) ]
   重要结论：
   y = U’XV= ΣΣu(i)x(ij)v(j) 于是 dy/dX = [u(i)v(j)] =UV’
   y = U’X’XU 则dy/dX = 2XUU’
   y =(XU-V)’(XU-V) 则 dy/dX = d(U’X’XU - 2V’XU + V’V)/dX = 2XUU’ - 2VU’ +0 = 2(XU-V)U’
9. 矩阵Y对矩阵X的导数：
   将Y的每个元素对X求导，然后排在一起形成超级矩阵。
   10.乘积的导数
   d(f*g)/dx=(df’/dx)g+(dg/dx)f’
   结论
   d(x’Ax)=(d(x”)/dx)Ax+(d(Ax)/dx)(x”)=Ax+A’x （注意：”是表示两次转置）

矩阵求导 属于 矩阵计算，应该查找 Matrix Calculus 的文献：
http://www.psi.toronto.edu/matrix/intro.html#Intro
http://www.psi.toronto.edu/matrix/calculus.html
http://www.stanford.edu/~dattorro/matrixcalc.pdf
http://www.colorado.edu/engineering/CAS/courses.d/IFEM.d/IFEM.AppD.d/IFEM.AppD.pdf
http://www4.ncsu.edu/~pfackler/MatCalc.pdf
http://center.uvt.nl/staff/magnus/wip12.pdf