矩阵零散知识总结3

1.XX^T结果生成一个对称矩阵

 

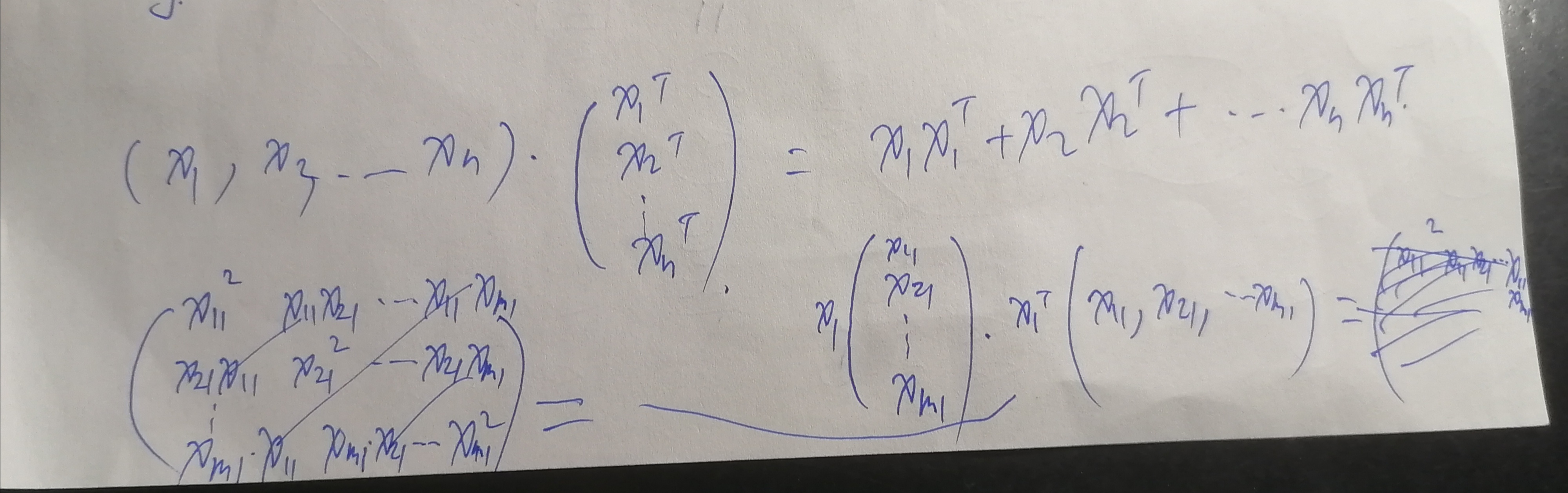
2. 在复数域内，一个实对称矩阵可以分解为另一个矩阵和他的转置的乘积吗？ 即A=BB^T？

可以说矩阵和bai他的转置的乘积是du一种构造实对称矩阵的zhi方法，但在实数范围内是不能构造所有实dao对称的，因为乘积矩阵对角线元素是矩阵B行向量与自身的内积，是非负的，所以对角线元素有负数的话在实数范围内是不能分解为另一个矩阵和他的转置的乘积的，但是把范围扩大到复数就可以了，因为复数的平方可以为的负，所以原命题成立

Cholesky 是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。它要求矩阵的所有特征值必须大于零，故分解的下三角的对角元也是大于零的。Cholesky分解法又称为平方根法，是当A为实对称正定矩阵时，LU三角分解法的变形。