人间四月芳菲尽,山寺桃花始盛开。
最近天气不错,但是想到同学都开始收二胎的份子钱了,顿感压力。
唉.....
由于搬家,本该上周就完成的,鸽了一周后还没完成。最近搬家,加上每天下班后还想忙点别的,真的是觉得时间不够用了,即使还是个单身狗。
简介
- 之前完成了简单的python驱动【coppeliasim】环境下搭建的机械臂。臂长是随便画的,所以这次在之前的基础上进一步优化机械臂,将臂长等参数确定下来,然后实现简单的界面控制。
实现
绘制机械臂:
如图,简单绘制长度准确的机械臂,臂长皆定义为:图中臂两端的圆心的距离。
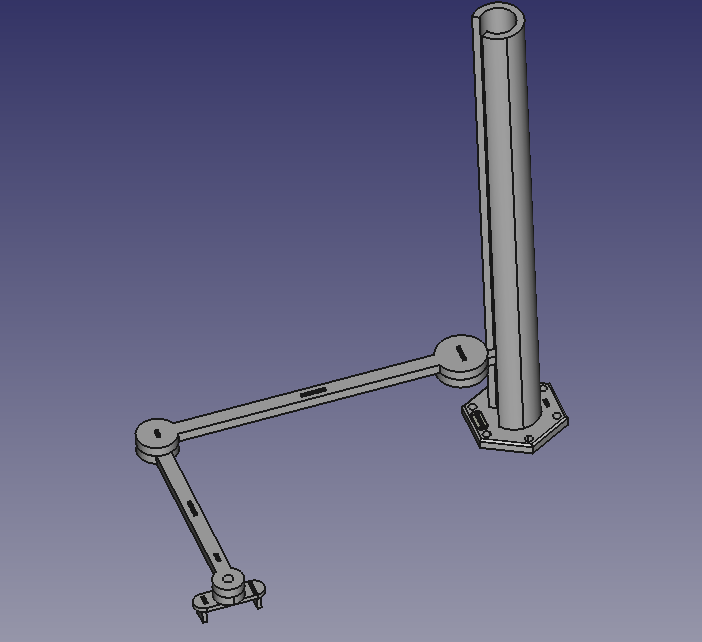
将【支架】的高度定义为50cm
将【支撑短臂】的长度定为5cm
将【第一长臂】的长度定义为30cm
将【第二短臂】的长度定义为20cm
此次,增加了一个简单的夹爪,只添加了旋转功能。
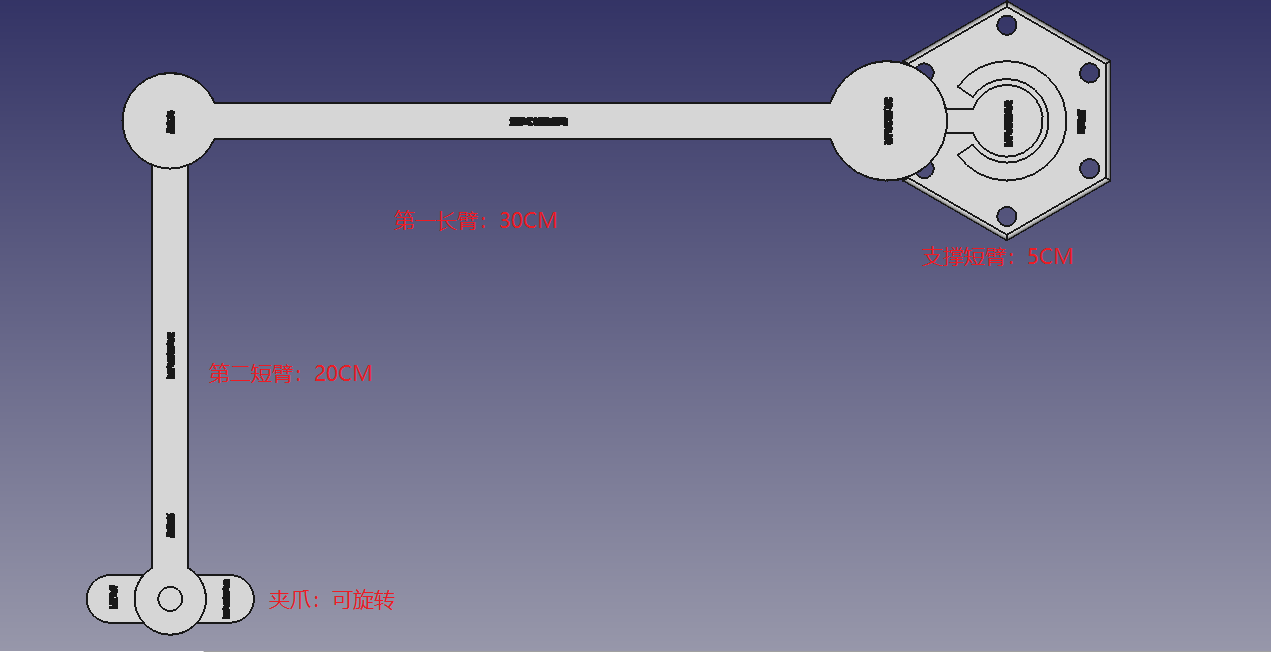
注意:为了避免与公司产品相同,此处建模都做简单的绘制处理用于示例;后面我还会修改机械臂类型或是关节数,使其与公司产品产生明显区别,后续的硬件、软件等内容也会尽可能的区别于公司方案,也会尽可能的从头实现。因为机械臂也是我一直想要实现的东西,而公司之前又有过这个项目,虽然暂时搁置,但我也不想因此有任何剽窃公司资源的嫌疑从而带来不必要的麻烦。
导入coppeliasim
导入【coppeliasim】,添加并移动好Joint后,放置对应的顺序关系,然后重命名。
因为本次增加了一个旋转夹爪,所以要多增加一个Joint。
在【Edit】中简化模型。此次加了字体,所以我简化为80%,太小字体就简化的看不到了。
名称修改和上一次的一致后,添加程序文件并添加远程端口函数,之前的程序就能直接用,若想控制夹爪旋转,只需要增加对应的关节名称即可操控。

为了美观,可以将Joint隐藏。选中Joint,双击或是【Tools->Scene Object Properties】,转到【Common】,将【Visibility】中的勾去掉即可:
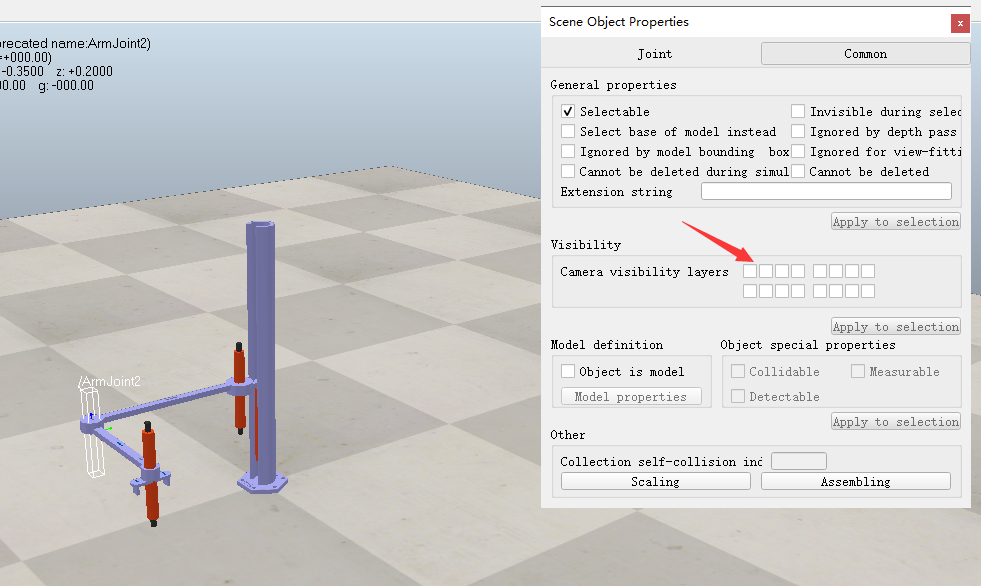
因为物理仿真相关的设置比较复杂,需要深入理解各选项和含义,所以本次模拟也不涉及物理属性。
PyQT界面
PyQT是QT框架的python绑定版本,目前支持到PyQT6,但PyQT5还比较常用。PyQT5提供GPL版和商业版证书,自由开发者可以使用免费的GPL许可,如果需要将PyQt用于商业应用,则必须购买商业许可。
实际上,比较推荐PySider6,使用LGPL协议,开源程度更友善,代码几乎完全兼容PyQT6.但是由于我习惯使用的是Anaconda的Spyder开发环境,其只支持PyQT开发(使用PySider会报错),所以后面都使用PyQT5开发。
使用【QTCreater】来绘制简单的操控界面:
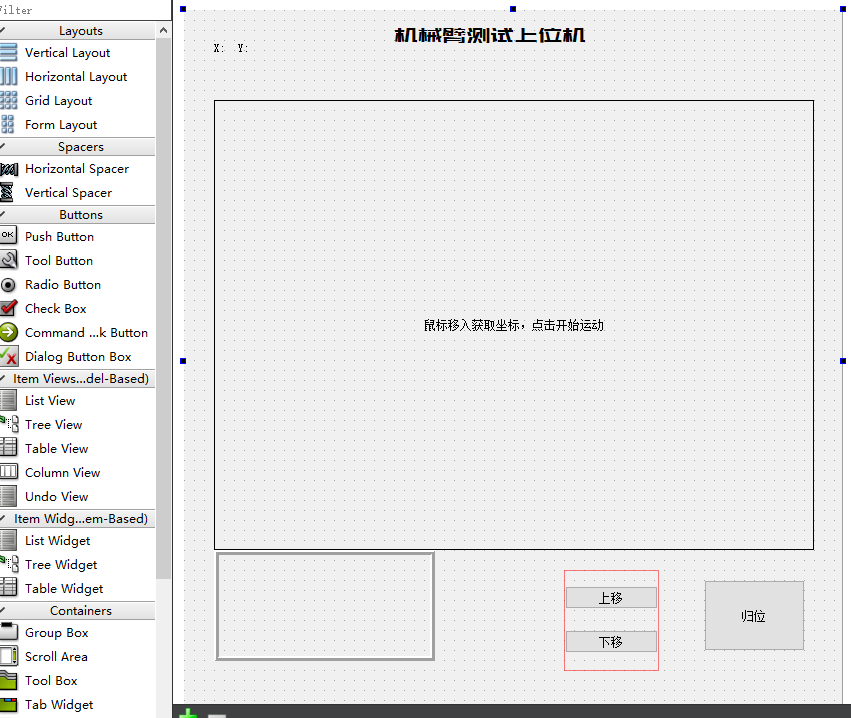
X Y坐标的实现
- 推荐书籍:《机器人学导论--分析、控制及应用》,《机器人学中的状态估计》
- 常用方法是将机械臂抽象成数学坐标矩阵,然后对应不同的参考坐标系,利用矩阵运算实现机器人的正逆运动学解算,然后转换回机械运动即可。
- 而我们目前的机械臂只是个最简单的运动模型,也因为时间关系,我先用简单的方法实现运动,矩阵实现的运动学解算放到后面实现。
- 另外,需要了解坐标系的知识,不同的参考坐标系之间坐标的转换等。本次测试使用固定坐标系,在俯视图中,以机械臂向下为默认方向,以【支撑短臂】与【第一长臂】的交点,即【ArmJoint1】为坐标原点,水平方向为X轴,竖直方向为Y轴,机械臂只在三四象限运动,即运动坐标范围为以50cm为半径,过(-50,0),(0,50),(50,0)三点的半圆范围:
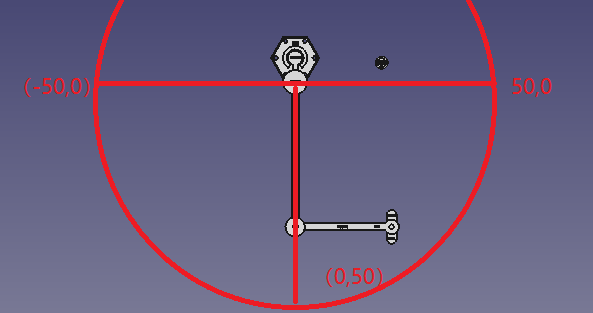
由于臂长不对等,所以原点周围的臂长差距范围也是移动不到的,就是以(0,0)为圆心,臂长差10cm为半径的圆。
简单实现的原理
我们要想机械臂运动到目标的X,Y坐标点,最终的目的就是要两个机械臂转到指定的角度。臂长已知,两个端点坐标已知。所以第一长臂的起点与第二短臂的末点,加上两个臂的交点,三个点,求出三角形的角度,就能得到两个臂需要转的角度,进而就能实现简单的坐标控制了。示意图如下:
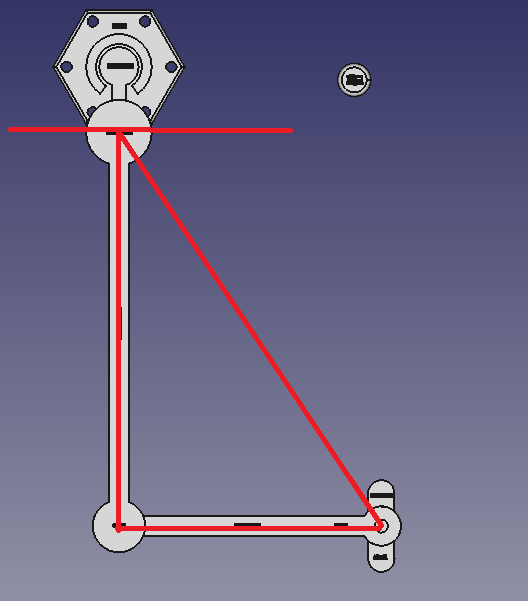
由于第一臂的转动会带动第二臂的转动,所以更好的求解示意图是抽象为两个圆。分别以第一臂的固定端点与第二臂的末点为圆心,以各自臂长为半径,抽象出两个圆,他们至少有一个交点(二者伸直),最多有两个交点(半径不同,所以不会重合),而其中一个交点就是转到指定坐标后第一臂与第二臂的交点位置:
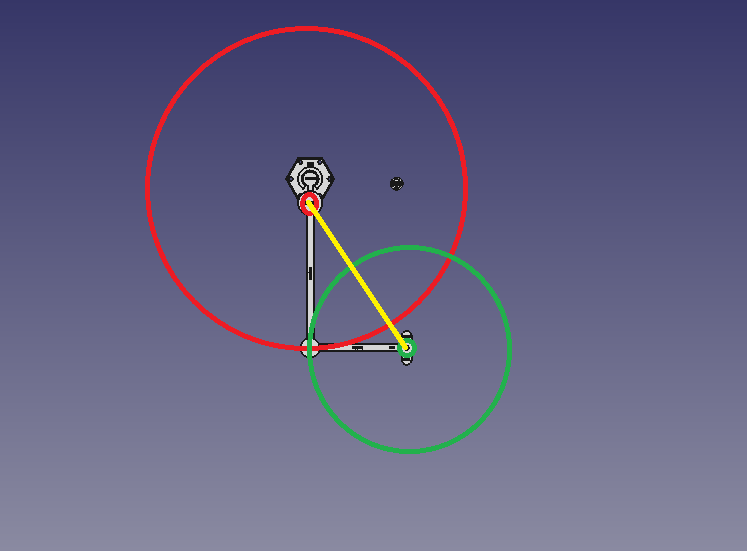
这样做的好处是,两个圆就是对应机械臂的运动范围,求出交点,就能很快得到第一臂的旋转角度,然后就能得到第二臂的旋转角度。
计算过程
已知参数如下:
第一臂长度:R1 = 30cm
第二臂长度:R2 = 20cm
坐标原点:(x1,y1)=(0,0),这个也是第一个圆的圆心坐标
目标点坐标:(x2,y2),这个也是第二个圆的圆心坐标
则根据圆心坐标可以求出两个圆的距离为 :
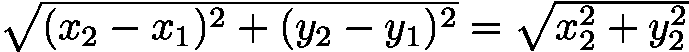
这个值可以用于判断有几个交点。
后面,可以用建立两个圆的标准方程进行联合进而求出交点的方法。
根据圆的一般方程:
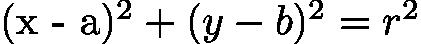
联立两个圆的方程,消掉x2和y2,得到直线的一般方程 y=kx+b,然后回带入任一圆的方程,即可解得交点坐标。
也可以用简单的三角形的三角关系来判定。
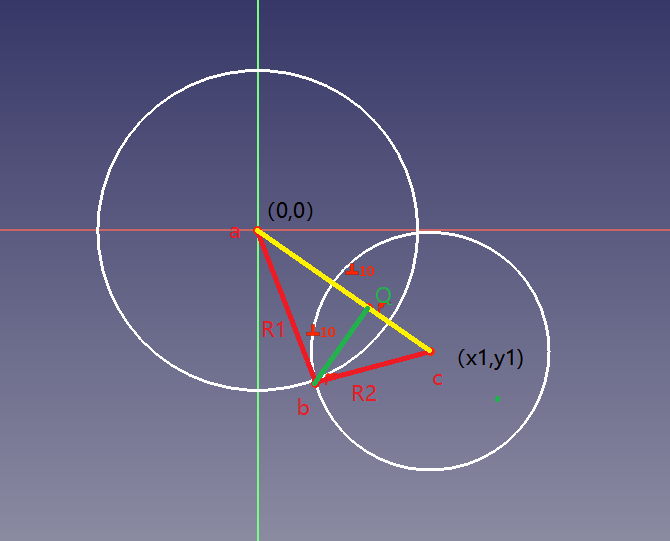
可以参考:【求解两圆的交点坐标】
然后根据坐标,求出两个臂的角度,发送给【coppeliasim】进行运动,就完成了。
对于第一个臂,已知斜边长=R和(x,y)坐标,根据三角函数就能求出角度。第二个臂一样,只不过坐标需要使用相对坐标来计算。另外要注意,第二臂的旋转角度是以X,Y轴计算的,所以在第一臂旋转后,第二臂的参考系也跟着旋转了,所以需要减去第一臂旋转的角度
绑定PyQT
完成坐标运动的解析后,就可以绑定到pyqt来实现一个简单的坐标控制了。
如图,实现一个用于获取坐标的界面,实现点击后,机械臂运动到所点击的位置:
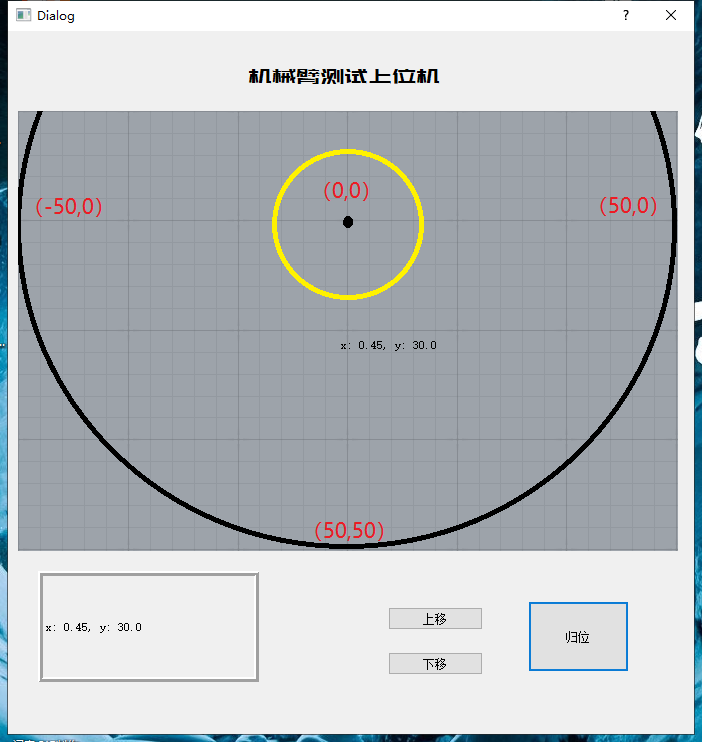
实际坐标大小与臂长范围大小需要换算。图片比例是660X440按照画图的方式进行一定比例的换算,得到圆内的坐标最大不超过(50,50)即可。可以自行更改图案宽比,也可以内部通过获取图片大小来设定界面大小,最后反向计算出合理的坐标值。此处为了简单,都用了固定的值进行计算。
由于时间关系,界面写的比较简单,按钮的功能也没加。本来计划在label中实现一个跟随鼠标移动的机械臂的,也没完成。后续如果时间充足,会加上。还会加上控制末端夹爪角度的按键。
另外,图内的圆的大小是随便画的,所以鼠标移动到内圈显示超出范围的点可能和内圈对应不上。
实现数据传递
可以在pyqt的代码中调用之前编写的机械臂控制相关的代码,将坐标发过去,即可进行机械臂控制。
由于时间关系,此处直接发送目标角度值,所以机械臂会直接运动过去。实际上,应该将运动分割开来,实现连续运动(实际上硬件上只需要发送最终的角度,电机就能直接运动过去,但是仿真软件只会直接运动到目标值,可能有中间过程的配置方式,我没找到。)所以后续会实现运动分割,实现连续运动。
总结
综上,我们就实现了一个最简单的到目标(x,y)点的运动仿真了,实现了基本的控制流程。后面可以更改为更加规范的矩阵坐标进行计算。
由于时间关系,坐标计算和点运动还有BUG没调试完成,所以点击获取坐标后,运动的位置并不对,周末再进行完善。
后续就是进行代码完善和转为更加正规的矩阵运算的方式,实现更加规范的代码逻辑。然后就是开始硬件相关的设计,直到完成机械臂实物。
以上模型和代码仓库地址: 【Gitee仓库】
-
本文水平有限,内容很多词语由于知识水平问题不严谨或很离谱,但主要作为记录作用,希望以后的自己和路过的大神对必要的错误提出批评与指点,对可笑的错误请指出来,我会改正的。
-
另外,转载使用请注明作者和出处,不要删除文档中的关于作者的注释。
随梦,随心,随愿,恒执念,为梦执战,执战苍天! ------------------执念执战





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY