【c++/c】反幂法求解绝对值最小的特征值

part 1：反幂法和LU分解

　　【反幂法】

　

 

 　　　　难点：对A进行LU分解。特别是程序编写过程中的下标。

　　　　【doolittle 分解】　　　

　　　　

 

 　　　　

 

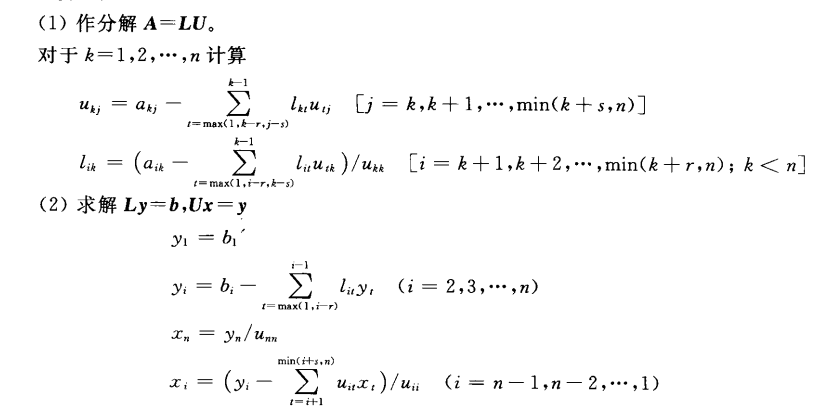
 　　【A->C】

　　　　对于大型n元带状线性方程组Ax=b。当n>>r+s+1（A的总带宽）时，为了节省存储量，A的带外元素不给存储，仅存A的带内元素。

　　　　　　

 

 　　　　　　

 

 point 2 程序的实现

#include <iostream>
#include <vector>
#include <math.h>
#include <cassert>
#include <iomanip>

using vec = std::vector<std::vector<double>>;
using vecRow = std::vector<double>;


/*
    定义一些全局变量
    g_r：矩阵A的下半带宽
    g_s：矩阵A的上半带宽
    g_time：迭代的最大次数，超出此数停止计算
    g_err：给定误差
*/
int g_r{ 2 };
int g_s{ 2 };
int g_time{ 5000 };
double g_err{ 10e-12 };

/*
    求a，b中的最小值
*/
int min(int a, int b) {
    return (a < b) ? a : b;
}


/*
    求最大值的函数重载
*/
int max(int a, int b, int c) {
    int max1{};
    (a > b) ? max1 = a : max1 = b;
    (max1 > c) ? max1 = max1 : max1 = c;
    return max1;
}

/*
    本题需要对int ，double两种类型的数进行处理
    因此使用了功能模板
*/
template <typename T>
T max(T a, T b) {
    return (a > b) ? a : b;
}

 

/*
    将矩阵A变为零矩阵
*/
vec changeZero(vec A) {
    int row{ static_cast<int> (A.size()) };
    int col{ static_cast<int>(A[0].size()) };
    for (int i = 0;i!=row;++i) {
        for (int j = 0;j != col;++j) {
            A[i][j] = 0.0;
        }
    }
    return A;
}

/*
    将向量A变为零向量
*/
vecRow changeZero(vecRow A) {
    int row{ static_cast<int> (A.size()) };
    for (int i = 0;i < row;++i) {
        A[i] = 0;
    }
    return A;
}

 

【将A矩阵变化为C矩阵】

vec createC(vec A) {
    int row{ static_cast<int> (A.size()) };
    int col{ static_cast<int>(A[0].size()) };
    int m{ g_r + g_s + 1 }; //5
    int n{ col }; //501
    vec C(m, vecRow(n));
    C = changeZero(C);
    int temp{};
    int start{};
    int end{};
    int mid{ g_s + 1  };//3
    int i{};// A矩阵的行
    int k{};// C矩阵的行
    for (int j = 0;j < n;j++) {  //j为A\C矩阵的列
        if (j < mid - 1) {
            start = mid - j - 1;//实际矩阵存放位置需要减去1
            end = m - start;
i = 0;
k = start;
while ((k < m) && (i < end)) {
    C[k][j] = A[i][j];
    ++i;
    ++k;
}
        }
       else if (j >= mid - 1 && j < n - g_r) {
       start = j - g_s;
       end = j + g_r + 1;
       i = start;
       k = 0;
       while ((i < end) && (k < m)) {
           C[k][j] = A[i][j];
           ++i;
           ++k;
       }

        }
       else if (j >= n - g_r) {
       start = j - g_r;
       end = n - start + 1;
       i = start;
       k = 0;
       while ((i < n) && (k < end)) {
           C[k][j] = A[i][j];
           ++i;
           ++k;
       }
        }
       else {
       continue;
        }
    }
    return C;
}

【将C矩阵进行LU分解】

//Doolittle 分解法 LU分解
vec dooLittleLU(vec C) {
    int row{ static_cast<int> (C.size()) };
    int col{ static_cast<int>(C[0].size()) };
    int m{ g_r + g_s + 1 };
    int n{ col };
    vecRow u(col);
    // LU分解，A->C
    //对于k=1,2，...，n计算
    int min1{};
    double sum{};
    int t0{};
    for (int k = 0;k < n;++k) {
        min1 = min((k + g_s), n - 1); //n需要-1，而k已经比原来小1了
        for (int j = k;j < min1 + 1;++j) {
            t0 = max(1 - 1, k - g_r, j - g_s);
            //t0 = (k > 2) * (k >= j) * (k - 2) + (j > 2) * (j > k) * (j - 2);
            for (int t = t0;t < k;++t) {
                //C[k - j + g_s + 1][j] = C[k - j + g_s + 1][j] - C[k - t + g_s + 1][t] * C[t - j + g_s + 1][j];
                //注意下标的转换，比公式上小1，因为从k=0开始计数
                C[k - j + g_s + 1 - 1][j] -= C[k - t + g_s + 1 - 1][t] * C[t - j + g_s + 1 - 1][j];
            }
        }
        if (k < n - 1) {
            min1 = min(k + g_r, n - 1);
            for (int i = k + 1;i < min1 + 1;++i) {
                //t0 = (k > 2) * (k >= i) * (k - 2) + (i > 2) * (i > k) * (i - 2);
                t0 = max(0, i - g_r, k - g_s);
                //sum = 0;
                for (int t = t0;t < k;++t) {
                    // std::cout << "mid: " << i - k + g_s + 1 - 1 << '\n';
                     // sum += C[i - t + g_s + 1][t] * C[t - k + g_s + 1][k];
                    C[i - k + g_s + 1 - 1][k] -= C[i - t + g_s + 1 - 1][t] * C[t - k + g_s + 1 - 1][k];
                }
                C[i - k + g_s + 1 - 1][k] = C[i - k + g_s + 1 - 1][k] / C[g_s + 1 - 1][k];
            }
        }

    }
    return C;
    //求解
}

【C矩阵回代，解方程】

vecRow dooLittleSolve(vec C, vecRow uk) {
    int row{ static_cast<int> (uk.size()) };
    int n{ row };
    int t0{};
    double min1{};
    for (int i = 2 - 1;i < row + 1 - 1;++i) {
        t0 = static_cast<int>(max(1 - 1, i - g_r));
        for (int t = t0;t < i - 1 + 1;++t) {
            uk[i] -= C[i - t + g_s + 1 - 1][t] * uk[t];
        }
    }
    uk[n - 1] = uk[n - 1] / C[g_s + 1 - 1][n - 1];
    for (int i = n - 1 - 1;i >= 0;--i) {
        min1 = min(i + g_s, n-1);
        for (int t = i + 1;t < min1 + 1;++t) {
            uk[i] -= C[i - t + g_s + 1 - 1][t] * uk[t];
        }
        uk[i] /= C[g_s + 1 - 1][i];
    }
    return uk;
}

【反幂法迭代求解】

double inverseMi(vec A, vecRow u0) {
    int row{ static_cast<int> (u0.size()) };
    vecRow y(row);
    vecRow uk(row);
    int m{ g_r + g_s + 1 };
    int n{ row };
    vec C(m, vecRow(n));
    double betak{};
    double beta0{};
    int t0{};
    double sum{};
    double min1{};
    C = createC(A);
    C = dooLittleLU(C); //LU分解
    //std::cout << "beta: " << betak << '\n';
    int k{ 1 };
    double distance{};
    while (k) {
        beta0 = betak;
        y = normalize(u0);
       // C = dooLittleLU(A); //LU分解
        uk = y;
        uk = dooLittleSolve(C, y);
        betak = 1 / multi(y, uk);
        distance = fabs((betak - beta0) / betak);
        if (distance <= g_err) {
            return betak;
        }
        if (k > g_time) {
            std::cout << "out of g_time" << '\n';
            return 0;
        }
        //std::cout << "step: " << k << '\n';
        u0 = uk;
        k++;
    }
    //return u;
    return betak;
 }

betak即为所求绝对值最小的特征值。