Trie字典树（前缀树）模版

1.Trie字典树/ 前缀树

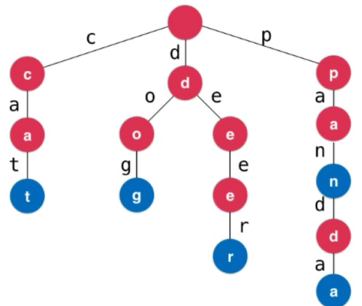
• 根节点没有字符路径。除根结点外每一个节点都被一个字符路径找到

• 从根节点出发到任何一个节点，如果将沿途经过的字符连接起来，一定为某个加入过的字符串的前缀

• 每个节点向下所有的字符路径上的字符都不同

 

public class Trie {

    private class TrieNode {
        public int path;　　//表示多少个单词共用这个节点
        public int end;　　 //表示多少个单词以这个节点结尾
        public TrieNode[] map;

        public TrieNode() {
            path = 0;
            end = 0;
            map = new TrieNode[26];
        }
    }

    private TrieNode root;

    public Trie() {
        root = new TrieNode();
    }

    //可重复添加一个单词
    public void insert(String word) {
        if (word == null) {
            return;
        }

        char[] chs = word.toCharArray();
        TrieNode node = root;
        node.path++;
        int index = 0;
        for (int i = 0; i < chs.length; i++) {
            index = chs[i] - 'a';
            if (node.map[index] == null) {
                node.map[index] = new TrieNode();
            }

            node = node.map[index];
            node.path++;
        }
        node.end++;
    }

    //查询word是否在字典树中
    public boolean search(String word) {
        if (word == null) {
            return false;
        }

        char[] chs = word.toCharArray();
        TrieNode node = root;
        int index = 0;
        for (int i = 0; i < chs.length; i++) {
            index = chs[i] - 'a';
            if (node.map[index] == null) {
                return false;
            }
            node = node.map[index];
        }
        return node.end != 0;
    }

    //返回以pre为前缀的单词数量
    public int prefixNumber(String pre) {
        if (pre == null) {
            return 0;
        }
        char[] chs = pre.toCharArray();
        TrieNode node = root;
        int index = 0;
        for (int i = 0; i < chs.length; i++) {
            index = chs[i] - 'a';
            if (node.map[index] == null) {
                return 0;
            }
            node = node.map[index];
        }
        return node.path;
    }

    //删除word，如果word添加过多次，仅删除一次
    public void delete(String word) {
        if (search(word)) {
            char[] chs = word.toCharArray();
            TrieNode node = root;
            node.path++;
            int index = 0;
            for (int i = 0; i < chs.length; i++) {
                index = chs[i] - 'a';
                if (node.map[index].path-- == 1) {
                    node.map[index] = null;
                    return;
                }
                node = node.map[index];
            }
            node.end--;
        }
    }

    public static void main(String[] args) {
        Trie trie = new Trie();
        trie.insert("e");
        trie.insert("efg");
        trie.insert("efg");
        trie.insert("efgij");
        trie.insert("a");
        trie.insert("ab");
        trie.insert("ad");

        System.out.println(trie.search("efg"));
        System.out.println(trie.search("efgh"));
        System.out.println(trie.prefixNumber("efg"));
        System.out.println(trie.prefixNumber("efgi"));
        System.out.println(trie.prefixNumber("a"));
        trie.delete("efg");
        System.out.println(trie.prefixNumber("efg"));
    }
}

2.字典树的变形

• 压缩字典树

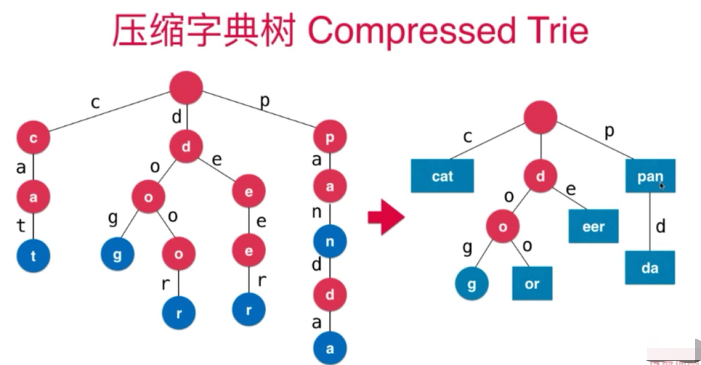
• 三分字典树

 

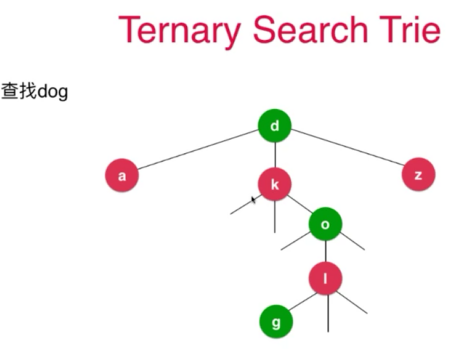
3.其他字符串问题

• 后缀树

• 子查询：KMP、Boyer-Moore、Rabin-Karp

• 文件压缩：哈夫曼树

• 模式匹配：正则表达式

• 编译原理、NLP、DNA