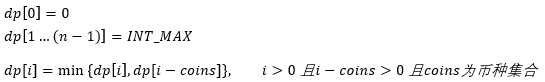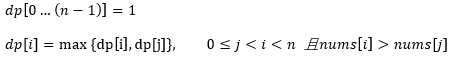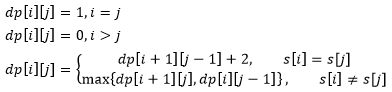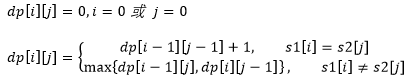1.遍历模版
public class Traversing {
public void print1(int n) {
System.out.println("按斜对角线从中间向右上打印矩阵");
for (int j = n; j > 0; j--) {
for (int i = 0; i < j; i++) {
System.out.print("(" + i + "," + (n - j + i) + ") ");
}
System.out.println();
}
}
public void print2(int n){
System.out.println("按列递增的自底向上打印");
for (int j = 0; j < n; j++) {
for (int i = j; i > -1; i--) {
System.out.print("(" + i + "," + j + ") ");
}
System.out.println();
}
}
public void print3(int n){
System.out.println("按行递减从左到右打印");
for (int i = n-1; i >= 0; i--) {
for (int j = i; j < n; j++) {
System.out.print("(" + i + "," + j + ") ");
}
System.out.println();
}
}
public static void main(String[] args) {
Traversing traversing = new Traversing();
System.out.println("都可以处理dp[i][j]由{dp[i+1][j-1](左下),dp[i][j-1](左),dp[i+1][j](下)}三个方向决定");
traversing.print1(5);
traversing.print2(5);
traversing.print3(5);
}
}
2.手法
-
动态规划题特点:最优子结构+重叠子问题+可以用自底向上的状态转移方程
-
明确状态->定义dp数组含义->明确状态转移方程->明确初始条件
3.典型例题
(1)使用最少硬币数的K钱(O(KN))
-
状态:dp[i]为i 钱需要最少的硬币数
-
初始化:dp[0]=0,dp[1...n-1] = INT_MAX
-
状态转移:利用所有dp[i - coins]的子状态求dp[i]状态,coins是币种集合,其中每个币种都有无限个
-
结果是dp[n],n钱需要最少的硬币数,当dp[n] = INT_MAX则不可用coins币种集合得到
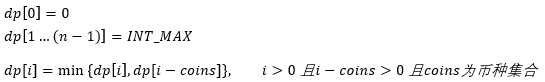
(2)最长递增子序列(动态规划:O(N2),二分查找:O(NlogN))
-
状态:dp[i]为以nums[i]结尾的最长递增子序列长度,其中i为子序列索引i,nums[i]为子序列索引i位置上的值
-
初始化:dp[0...n-1] = 1,每个数都以自己结尾至少长度为1
-
状态转移:利用所有的dp[j],其中j<i并且只有在nums[i] > nums[j]才处理
-
结果是max{dp[i]},获得dp数组中最大值
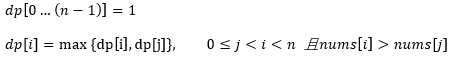
(3)最长回文子序列长度(动态规划:O(N2) ,存在更优算法)
-
状态:dp[i][j]为s[i...j]字符串最长回文子序列长度,其中s为需要查找的字符串
-
初始化:dp[0][0] = dp[1][1] = ... = dp[n-1][n-1] = 1,一个字符本身就是回文串长度为1;当s[i...j]中j<i,则dp[i][j] = 0
-
状态转移:当s[i]=s[j]时,利用已知s[(i+1)...(j-1)]串中最大长度来扩大s[i...j]最大长度,当s[i] != s[j]时,说明s[i]和s[j]两者最多只有一个存在于s[i...j]的最大回文子序列中得,可利用s[(i+1)...j]和s[i...(j-1)]串中最大长度得到s[i...j]最大长度
-
结果是s[0...(n-1)]获得从0到n-1的串最长回文子序列长度
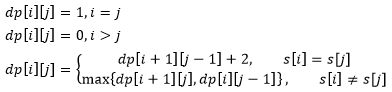
(4)最小编辑距离(动态规划:O(N2))
-
状态:dp[i][j]为将s1[0...i]变为s2[0...j]的最小编辑距离(s1串不变(+0),删除一个(+1),插入一个(+1),替换一个(+1),此处字符串下标从1开始,0为空串)
-
初始化:dp[i][0] = i,当s2[0...0] 则将s1[0....i]串删除i次;dp[0][j] = j,当s1[0...0] 则将s1串一直插入字符直到得到s2[0...j],插入j次
-
状态转移:当s1[i]=s2[j]时,利用已知dp[i-1][j-1]的编辑距离(不变),当s1[i] != s2[j]时,说明需要删除或插入或替换
-
删除:将s1[0...i]中的s1[i]删除,利用dp[i-1][j]得到dp[i][j] = dp[i-1][j] + 1
-
插入:将s1[0...i]最后插入s2[j],利用dp[i][j-1]得到dp[i][j] = dp[i][j-1] + 1
-
替换:将s1[0...i]中的s1[i]替换成s2[j],利用dp[i-1][j-1]得到dp[i][j] = dp[i-1][j-1] + 1
-
获得到最小的dp[i][j]
-
结果是dp[len(s1)][len(s2)]

int minDistance(String s1, String s2) {
int m = s1.length(), n = s2.length();
int[][] dp = new int[m + 1][n + 1];
// base case
for (int i = 1; i <= m; i++)
dp[i][0] = i;
for (int j = 1; j <= n; j++)
dp[0][j] = j;
// ⾃底向上求解
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
if (s1.charAt(i-1) == s2.charAt(j-1))
dp[i][j] = dp[i - 1][j - 1];
else
dp[i][j] = min(
dp[i - 1][j] + 1,
dp[i][j - 1] + 1,
dp[i-1][j-1] + 1
);
// 储存着整个 s1 和 s2 的最⼩编辑距离
return dp[m][n];
}
int min(int a, int b, int c) {
return Math.min(a, Math.min(b, c));
}
(5)最长公共子序列LCS
-
状态:dp[i][j]为s1[0...i]与s2[0...j]的最长公共子序列(字符串下标的序号从1开始,0为空串)
-
初始化:dp[0][...] = dp[...][0] = 0,两者之一为空串最长公共子序列长度都为0
-
状态转移:
-
当s1[i]=s2[j]时,利用已有的dp[i-1][j-1]在其长度上加1,s1[0...i-1]与s2[0...j-1]同时都向后增长一位
-
当s1[i] != s2[j],利用已有的dp[i][j-1]或dp[i-1][j],要么s1[0...i-1]增长一位或s2[0...j-1]增长一位
-
结果是dp[len(s1)][len(s2)]得到LCS长度
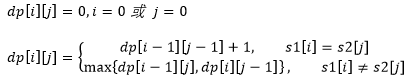
public int[][] genLCSdp(String s1, String s2) {
int len1 = s1.length();
int len2 = s2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp;
}
public String getLCS(int[][] dp, String s1) {
int row = dp.length - 1;
int col = dp[0].length - 1;
int lenLCS = dp[row][col];
char[] lcs = new char[lenLCS];
while (lenLCS > 0) {
if (dp[row][col] == dp[row - 1][col]) {
row--;
} else if (dp[row][col] == dp[row][col - 1]) {
col--;
} else {
row--;
col--;
lcs[--lenLCS] = s1.charAt(row);
}
}
return String.valueOf(lcs);
}