博弈问题dp模版
博弈问题动态规划通用思路
转载:来自大佬https://leetcode-cn.com/problems/stone-game/solution/jie-jue-bo-yi-wen-ti-de-dong-tai-gui-hua-tong-yong/
-
该问题主要是如何设计dp数组,其次是动态转移方程
1.dp数组设计
-
状态有三种:开始堆的索引i,结束堆的索引j,以及当前轮到的人
dp[i][j].fir 表示,对于 piles[i...j] 这部分石头堆,先手能获得的最高分数。
dp[i][j].sec 表示,对于 piles[i...j] 这部分石头堆,后手能获得的最高分数。
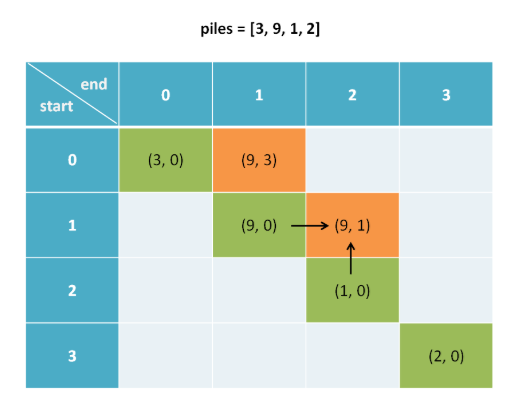
举例理解一下,假设 piles = [3, 9, 1, 2],索引从 0 开始
dp[0][1].fir = 9 意味着:面对石头堆 [3, 9],先手最终能够获得 9 分。
dp[1][3].sec = 2 意味着:面对石头堆 [9, 1, 2],后手最终能够获得 2 分。
2.动态转移方程
-
状态不断转换:A选手从[i,...,j]堆中先手取完之后,B选手则从[i+1,...,j]或[i,....,j-1]堆中先手取,这样交替进行。
-
A选手:
-
A选手从[i,...,j]堆中先手取完之后,A选手的状态将变为从[i+1,...,j]或[i,....,j-1]堆中后手取
-
如果A选手想要先手,则可得的最高分数 dp[i][j].fir = max(piles[i] + dp[i+1][j].sec,piles[j] + dp[i][j-1].sec)
-
-
B选手:
-
B选手则从[i+1,...,j]或[i,....,j-1]堆中先手取的状态等价于B选手从[i,...,j]堆中后手取。
-
如果剩余[i+1,...,j],则dp[i][j].sec = dp[i+1][j].fir
-
如果剩余[i,...,j-1],则dp[i][j].sec = dp[i][j-1].fir
-
dp[i][j].fir = max(piles[i] + dp[i+1][j].sec, piles[j] + dp[i][j-1].sec)
dp[i][j].fir = max( 选择最左边的石头堆 , 选择最右边的石头堆 )
# 解释:我作为先手,面对 piles[i...j] 时,有两种选择:
# 要么我选择最左边的那一堆石头,然后面对 piles[i+1...j]
# 但是此时轮到对方,相当于我变成了后手;
# 要么我选择最右边的那一堆石头,然后面对 piles[i...j-1]
# 但是此时轮到对方,相当于我变成了后手。
if 先手选择左边:
dp[i][j].sec = dp[i+1][j].fir
if 先手选择右边:
dp[i][j].sec = dp[i][j-1].fir
# 解释:我作为后手,要等先手先选择,有两种情况:
# 如果先手选择了最左边那堆,给我剩下了 piles[i+1...j]
# 此时轮到我,我变成了先手;
# 如果先手选择了最右边那堆,给我剩下了 piles[i...j-1]
# 此时轮到我,我变成了先手。
3.初始条件
-
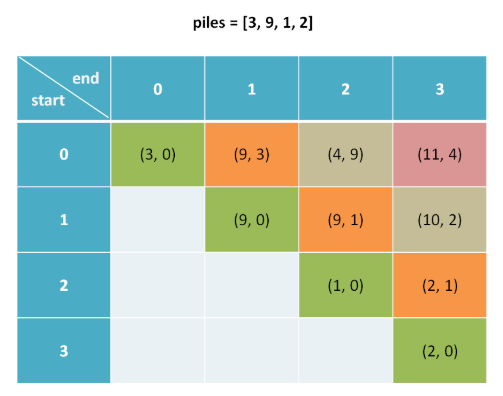
由动态转移方程可知,dp[i][j]由左侧dp[i][j-1]和下侧dp[i+1][j]决定,则要先初始化斜对角线元素,最终求得dp[0][n-1],比较dp[0][n-1].fir与dp[0][n-1].sec哪个大,哪个大就是获胜方
4.代码
-
n*n的矩阵(可有为1维,但是n维操作更加清晰)
class Pair { int fir, sec; Pair(int fir, int sec) { this.fir = fir; this.sec = sec; } } class Solution { /* 返回游戏最后先手和后手的得分之差 */ public boolean stoneGame(int[] piles) { int n = piles.length; // 初始化 dp 数组 Pair[][] dp = new Pair[n][n]; for (int i = 0; i < n; i++) for (int j = i; j < n; j++) dp[i][j] = new Pair(0, 0); // 填入基本数据(斜对角线数据) for (int i = 0; i < n; i++) { dp[i][i].fir = piles[i]; dp[i][i].sec = 0; } // 斜着遍历数组 for (int l = 2; l <= n; l++) { //斜对角线元素个数从n-1开始递减 for (int i = 0; i <= n - l; i++) { //行从[0,...,n-2]开始缩小 int j = l + i - 1; // 先手选择最左边或最右边的分数 int left = piles[i] + dp[i + 1][j].sec; int right = piles[j] + dp[i][j - 1].sec; // 套用状态转移方程 if (left > right) { dp[i][j].fir = left; dp[i][j].sec = dp[i + 1][j].fir; } else { dp[i][j].fir = right; dp[i][j].sec = dp[i][j - 1].fir; } } } Pair res = dp[0][n - 1]; return res.fir > res.sec; } }
-
1*n矩阵
class Pair { int fir, sec; Pair(int fir, int sec) { this.fir = fir; this.sec = sec; } } class Solution { /* 返回游戏最后先手和后手的得分之差 */ public boolean stoneGame(int[] piles) { int n = piles.length; // 初始化 dp 数组 Pair[] dp = new Pair[n]; for (int i = 0; i < n; i++) { dp[i] = new Pair(0, 0); } // 遍历数组 for (int i = n - 1; i >= 0; i--) { for (int j = i; j < n; j++) { if(i == j){ // 填入基本数据(斜对角线数据) dp[j].fir = piles[i]; dp[j].sec = 0; }else { int d1 = piles[i] + dp[j].sec; int d2 = piles[j] + dp[j - 1].sec; if (d1 > d2) dp[j].sec = dp[j].fir; //这里要用到dp[j].fir的旧值 else dp[j].sec = dp[j - 1].fir; dp[j].fir = Math.max(d1, d2); //注意这行,必须要在dp[j].sec赋值完才能执行,因为上面可能会用到它的旧值 } } } Pair res = dp[n - 1]; return res.fir > res.sec; } }





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET 9 new features-C#13新的锁类型和语义
· Linux系统下SQL Server数据库镜像配置全流程详解
· 现代计算机视觉入门之:什么是视频
· 你所不知道的 C/C++ 宏知识
· 聊一聊 操作系统蓝屏 c0000102 的故障分析
· 不到万不得已,千万不要去外包
· C# WebAPI 插件热插拔(持续更新中)
· 会议真的有必要吗?我们产品开发9年了,但从来没开过会
· 如何打造一个高并发系统?
· 《SpringBoot》EasyExcel实现百万数据的导入导出