斐波那契的状态矩阵【快速幂+矩阵乘积】

斐波那契的状态矩阵，求解时间复杂度O(logN)

由f(n) = f(n-1) + f(n-2)，f(n-1) = f(n-1)

得（f(n)，f(n-1)） =（f(n-1) + f(n-2)，f(n-1)）得到关于（f(n-1)，f(n-2)）系数行列式，自底向上推出方程即可

得到(f(n),f(n-1)) = (f(2),f(1)) *系数矩阵【【1,1】，【1,0】】^n-2 可得

 

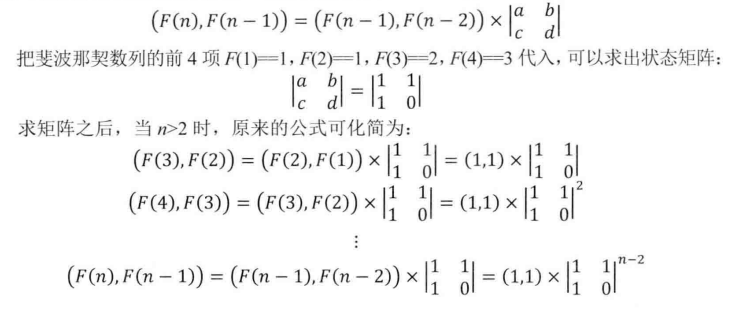
 程序代码：

public class Fibonacci {
    //m*n 与 n*s 得到m*s
    public int[][] multiplyMatrix(int[][] m1, int[][] m2) {
        int[][] res = new int[m1.length][m2[0].length];
        for (int i = 0; i < m1.length; i++) {
            for (int j = 0; j < m2[0].length; j++) {
                for (int k = 0; k < m2.length; k++) {
                    res[i][j] += m1[i][k] * m2[k][j];
                }
            }
        }
        return res;
    }

    //矩阵m的p次方
    public int[][] matrixPower(int[][] m, int p) {
        int[][] res = new int[m.length][m[0].length];

        //设置res为单位矩阵，任意矩阵乘以单位矩阵还是任意矩阵
        for (int i = 0; i < res.length; i++) {
            res[i][i] = 1;
        }

        int[][] tmp = m;
        while (p > 0) {
            if ((p & 1) != 0) {
                res = multiplyMatrix(res, tmp);
            }
            tmp = multiplyMatrix(tmp, tmp);
            p >>= 1;
        }
        return res;
    }

    //O(logN)得到斐波那契值
    public int f(int n) {
        if (n < 1) {
            return 0;
        }
        if (n == 1 || n == 2) {
            return 1;
        }

        int[][] base = {{1, 1}, {1, 0}};
        int[][] res = matrixPower(base, n - 2);
        return res[0][0] + res[1][0];
    }

    public static void main(String[] args) {
        Fibonacci fibonacci = new Fibonacci();
        System.out.println(fibonacci.f(5));
    }

}

 再举一个例子求解系数矩阵

递推公式：f(n) = f(n-1) + f(n-3)

列方程：

f(n) = 1*f(n-1) + 0*f(n-2) + 1*f(n-3)

f(n-1) = 1*f(n-1) + 0*f(n-2) + 0*f(n-3)

f(n-2) = 0*f(n-1) + 1*f(n-2) + 0*f(n-3)

得到(f(n),f(n-1),f(n-2)) 关于(f(n-1),f(n-2),f(n-3))的系数行列式：注意是一行乘以一列，等式右边系数按照列排列

1  1  0
0  0  1
1  0  0