线段树模版

题目：https://leetcode-cn.com/problems/range-sum-query-mutable/

给定一个整数数组  nums，求出数组从索引 i 到 j  (i ≤ j) 范围内元素的总和，包含 i,  j 两点。

update(i, val) 函数可以通过将下标为 i 的数值更新为 val，从而对数列进行修改。

示例:

Given nums = [1, 3, 5]

sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8

说明:

1.数组仅可以在 update 函数下进行修改。
2.你可以假设 update 函数与 sumRange 函数的调用次数是均匀分布的。

思路：

 

 

 

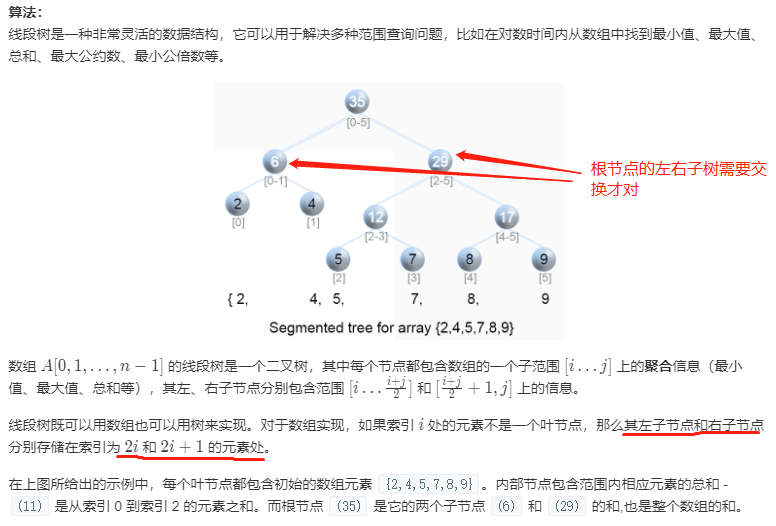
线段树可以分为以下三个步骤：

1. 从给定数组构建线段树的预处理步骤。
2. 修改元素时更新线段树。
3. 使用线段树进行区域和检索。

 

 

 

 

 

 

 

 

 

//经典题型：线段树
public class P307RangeSumQueryMutable {

    public static void main(String[] args) {

        NumArray obj = new NumArray(new int[]{1, 3, 5, 8});
        System.out.println(obj.sumRange(0, 3));
        obj.update(1, 2);
        System.out.println(obj.sumRange(0, 3));
    }

    static class NumArray {

        int[] arr;
        int numsLength;

        //构建：初始化线段树[n,2n)和(0,n-1]，一共有2n-1个数据，从[n,2n-1]的是输入的nums，从[1,n-1]是计算出的线段和
        public NumArray(int[] nums) {
            int len = nums.length;
            if (len > 0) {
                arr = new int[2 * len];
                numsLength = len;
                for (int i = len; i < 2 * len; i++) {
                    arr[i] = nums[i - len];
                }

                //从后向前计算arr[i] = arr[2*i] + arr[2*i + 1]，左节点为偶数节点，右节点为奇数节点
                for (int i = len - 1; i > 0; i--) {
                    arr[i] = arr[2 * i] + arr[2 * i + 1];
                }
            }
        }

        //每次更新都要从下向上更新父节点直至根节点
        public void update(int i, int val) {
            //先计算节点在arr数组的位置
            int position = i + numsLength;
            arr[position] = val;

            //从下向上更新到根节点
            while (position > 0) {
                //当前在左节点
                if ((position % 2) == 0) {
                    arr[position / 2] = arr[position] + arr[position + 1];
                } else { //当前在右节点
                    arr[position / 2] = arr[position - 1] + arr[position];
                }

                //向上为父节点
                position /= 2;
            }
        }

　　　　　　
        //区域和检索：每次确保左边界为偶数，右边界为奇数然后同时除以2
        //如果左边界不为偶数，则当前和加上当前左边界值，左边界向右移动一位，然后除以2
        //如果右边界不为奇数，则当前和加上当前右边界值，右边界向左移动一位，然后除以2
        //直到左边界大于右边界截止
        public int sumRange(int i, int j) {

            int sum = 0;
            //移动到arr正确的位置上
            i += numsLength;
            j += numsLength;

            while (i <= j) {

                //左边界为奇数
                if ((i % 2) == 1) {
                    sum += arr[i];
                    i++;
                }

                //右边界为偶数
                if ((j % 2) == 0) {
                    sum += arr[j];
                    j--;
                }

                i /= 2;
                j /= 2;
            }

            return sum;
        }
    }
}

 

 

 

 

 

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/range-sum-query-mutable