动态规划经典题型

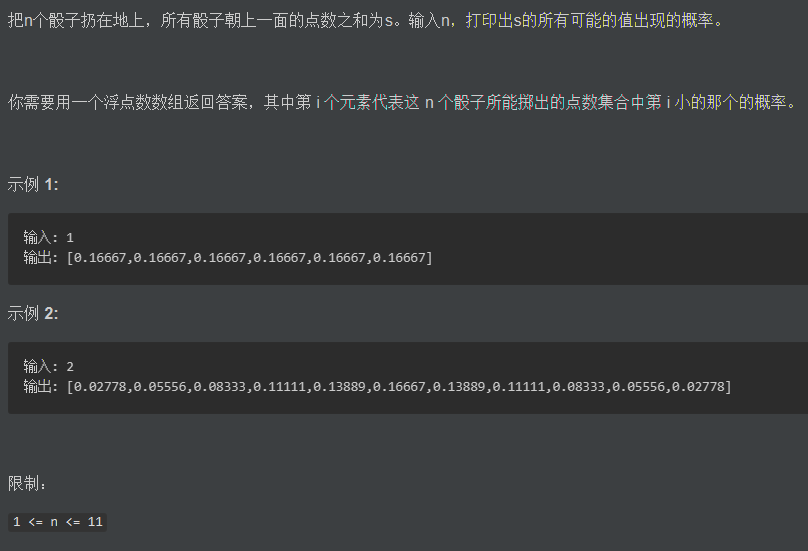
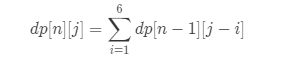一.问题

  • https://leetcode-cn.com/problems/nge-tou-zi-de-dian-shu-lcof/：面试题60：n个骰子的点数

 

 

 二.解法

  • 动态规划：用 dp[n][j] 来表示n个骰子的点数 j 出现的次数。

  • 状态转移方程：表示n个骰子产生的点数 j 出现的次数等于n-1个骰子产生 j - 1, j - 2, j - 3, j - 4, j - 5, j - 6 次数之和

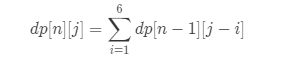
  • 基本步骤：1.先设立参数以及参数对应的意义，2.写出动态转移方程，3.设置初始状态值

1.代码一：

class Solution {
public:
    vector<double> twoSum(int n) {
        int dp[15][70];
        memset(dp, 0, sizeof(dp));
        for (int i = 1; i <= 6; i ++) {
            dp[1][i] = 1;
        }
        for (int i = 2; i <= n; i ++) {
            for (int j = i; j <= 6*i; j ++) {
                for (int cur = 1; cur <= 6; cur ++) {
                    if (j - cur <= 0) {
                        break;
                    }
                    dp[i][j] += dp[i-1][j-cur];
                }
            }
        }
        int all = pow(6, n);
        vector<double> ret;
        for (int i = n; i <= 6 * n; i ++) {
            ret.push_back(dp[n][i] * 1.0 / all);
        }
        return ret;
    }
};

2.代码二

  • 优化二维数组变为一维数组：方法是从后向前修改值，保证前一维的值不变来得到后一维的值

class Solution {
public:
    vector<double> twoSum(int n) {
        int dp[70];
        memset(dp, 0, sizeof(dp));
        for (int i = 1; i <= 6; i ++) {
            dp[i] = 1;
        }
        for (int i = 2; i <= n; i ++) {
            for (int j = 6*i; j >= i; j --) {
                dp[j] = 0;
                for (int cur = 1; cur <= 6; cur ++) {
                    if (j - cur < i-1) {
                        break;
                    }
                    dp[j] += dp[j-cur];
                }
            }
        }
        int all = pow(6, n);
        vector<double> ret;
        for (int i = n; i <= 6 * n; i ++) {
            ret.push_back(dp[i] * 1.0 / all);
        }
        return ret;
    }
};

三.思路和代码来自：

作者：huwt
链接：https://leetcode-cn.com/problems/nge-tou-zi-de-dian-shu-lcof/solution/nge-tou-zi-de-dian-shu-dong-tai-gui-hua-ji-qi-yo-3/

 

posted @ 2020-03-25 23:47  All_just_for_fun  阅读(167)  评论(0)  编辑  收藏  举报