机器学习-02-数据清洗和特征选择
一、缺省值填充
1. 老版本用Imputer
import numpy as np from sklearn.preprocessing import Imputer X = [ [2, 2, 4, 1], [np.nan, 3, 4, 4], [1, 1, 1, np.nan], [2, 2, np.nan, 3] ] # missing_values(缺失值),strategy(策略,默认平均值),axis(选择行列,0为列,1为行)
#– 均值mean(默认方法)
# – 中位数median
#– 众数most_frequent
imp1 = Imputer(missing_values='NaN', strategy='mean', axis=0) # 缺省值选择空,策略为平均数,
imp2 = Imputer(missing_values='NaN', strategy='mean', axis=1)
print(imp1.fit_transform(X))
print(imp2.fit_transform(X))
[[2. 2. 4. 1. ]
[1.66666667 3. 4. 4. ]
[1. 1. 1. 2.66666667]
[2. 2. 3. 3. ]]
[[2. 2. 4. 1. ]
[3.66666667 3. 4. 4. ]
[1. 1. 1. 1. ]
[2. 2. 2.33333333 3. ]]
2. 新版本用 SimpleImputer
1 import numpy as np 2 from sklearn.preprocessing import Imputer 3 from sklearn.impute import SimpleImputer 4 5 X = [ 6 [2, 2, 4, 1], 7 [np.nan, 3, 4, 4], 8 [1, 1, 1, np.nan], 9 [2, 2, np.nan, 3] 10 ] 11 # 参数详解可见,暂未发现选择行操作 12 # http://scikit-learn.org/dev/modules/generated/sklearn.impute.SimpleImputer.html 13 imp1 = SimpleImputer(missing_values='NaN', strategy='mean') 14 print(imp1.fit_transform(X))
[[2. 2. 4. 1. ]
[1.66666667 3. 4. 4. ]
[1. 1. 1. 2.66666667]
[2. 2. 3. 3. ]]
二、编码
1. 哑编码(独热编码)
# 独热编码 import numpy as np from sklearn.preprocessing import OneHotEncoder from sklearn.feature_extraction import DictVectorizer,FeatureHasher enc = OneHotEncoder() enc.fit([[0, 0, 3], [1, 1, 0], [0, 2, 1], [1, 0, 2]]) a=np.array([[0, 0, 3], [1, 1, 0], [0, 2, 1], [1, 0, 2]]) print(a) # 基于列进行编码,打印有多少种值 print(enc.n_values_) # 把0放到第一列[0,1]比对,把1放到第二列[0,1,2]比对,把3放到第三列[0,1,2,3]比对 print(enc.transform([[0, 1, 3]]).toarray())
[[0 0 3]
[1 1 0]
[0 2 1]
[1 0 2]]
[2 3 4]
[[1. 0. 0. 1. 0. 0. 0. 0. 1.]]
2. 标签编码
# 标签编码 from sklearn.preprocessing import LabelEncoder le = LabelEncoder() le.fit_transform([1,5,6,100,67]) print('编码结果是:', le.transform([1,1,100,67,5]))
print(le.fit(["paris", "paris", "tokyo", "amsterdam"])) print(list(le.classes_)) print(le.transform(["tokyo", "tokyo", "paris"])) print(list(le.inverse_transform([2, 2, 1]))) # 逆过程
编码结果是: [0 0 4 3 1]
LabelEncoder()
['amsterdam', 'paris', 'tokyo']
[2 2 1]
['tokyo', 'tokyo', 'paris']
3. 将特征值映射列表转换为向量
from sklearn.feature_extraction import DictVectorizer dv = DictVectorizer(sparse=False) D = [{'foo':1, 'bar':2}, {'foa':3, 'baz': 2}] X = dv.fit_transform(D) print (X) print (dv.get_feature_names()) print (dv.transform({'foo':4, 'unseen':3,'baz':10})) [[2. 0. 0. 1.] [0. 2. 3. 0.]] ['bar', 'baz', 'foa', 'foo'] [[ 0. 10. 0. 4.]]
4. hash转换
from sklearn.feature_extraction import FeatureHasher h = FeatureHasher(n_features=10,non_negative=True) # n_features:多少个特征,non_negative:是不是正数 D = [{'dog': 1, 'cat':2, 'elephant':4},{'dog': 2, 'run': 5}] f = h.fit_transform(D) print(f.toarray())
[[0. 0. 4. 1. 0. 0. 0. 0. 0. 2.]
[0. 0. 0. 2. 5. 0. 0. 0. 0. 0.]]
三、二值化
import numpy as np from sklearn.preprocessing import Binarizer arr = np.array([ [1.5, 1.3, 1.9], [0.5, 0.5, 1.6], [1.1, 2.1, 0.2] ]) binarizer = Binarizer(threshold=1.0).fit_transform(arr) print(binarizer)
[[1. 1. 1.]
[0. 0. 1.]
[1. 1. 0.]]
四、标准化
在很多模型中,假设各特征的取值区间相同。如果数据不满足该假设,需要将数据进行变换。
标准化是一种常用数据转换方式,将输入特征减去该特征的均值后,在除以其标准差。可用类StandardScaler实现

'''作用:去均值和方差归一化。且是针对每一个特征维度来做的,而不是针对样本。 【注:】 并不是所有的标准化都能给estimator带来好处。 (x-x.mean())/x.std() 本方法要求原始数据的分布可以近似为高斯分布,否则归一化的效果会变得很糟糕; 应用场景:在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候''' from sklearn.preprocessing import StandardScaler import pandas as pd X = [ [1, 2, 3, 2], [7, 8, 9, 2.01], [4, 8, 2, 2.01], [9, 5, 2, 1.99], [7, 5, 3, 1.99], [1, 4, 9, 2] ] ss = StandardScaler(with_mean=True, with_std=True) ss.fit(X) print(ss.mean_) print(ss.n_samples_seen_) print(ss.scale_) print(ss.transform(X)) y = pd.DataFrame(X) z = y.apply(lambda x:(x - x.mean())/x.std()) print(z) w = y.apply(lambda x:(x - x.mean())/x.std(ddof=0)) # 修正因子,做标准差是padas默认无偏差估计 print(w)
[4.83333333 5.33333333 4.66666667 2. ]
6
[3.07769755 2.13437475 3.09120617 0.00816497]
[[-1.24551983 -1.56173762 -0.53916387 0. ]
[ 0.70398947 1.2493901 1.40182605 1.22474487]
[-0.27076518 1.2493901 -0.86266219 1.22474487]
[ 1.3538259 -0.15617376 -0.86266219 -1.22474487]
[ 0.70398947 -0.15617376 -0.53916387 -1.22474487]
[-1.24551983 -0.62469505 1.40182605 0. ]]
0 1 2 3
0 -1.136999 -1.425665 -0.492187 0.000000
1 0.642652 1.140532 1.279686 1.118034
2 -0.247174 1.140532 -0.787499 1.118034
3 1.235868 -0.142566 -0.787499 -1.118034
4 0.642652 -0.142566 -0.492187 -1.118034
5 -1.136999 -0.570266 1.279686 0.000000
0 1 2 3
0 -1.245520 -1.561738 -0.539164 0.000000
1 0.703989 1.249390 1.401826 1.224745
2 -0.270765 1.249390 -0.862662 1.224745
3 1.353826 -0.156174 -0.862662 -1.224745
4 0.703989 -0.156174 -0.539164 -1.224745
5 -1.245520 -0.624695 1.401826 0.000000
五、数据正规化

六、区间缩放
适用比较适用在数值比较集中的情况
缺陷:如果max和min不稳定,很容易使得归一化结果不稳定,使得后续使用效果也不稳定。实际使用中可以用经验常量来替代max和min。
应用场景:在不涉及距离度量、协方差计算、数据不符合正太分布的时候,可以使用第一种方法或其他归一化方法(不包括Z-score方法)。比如图像处理中,将RGB图像转换为灰度图像后将其值限定在[0 255]的范围
# 区间缩放 import numpy as np from sklearn.preprocessing import MinMaxScaler X = np.array([ [1, -1, 2, 3], [2, 0, 0, 3], [0, 1, -1, 3] ], dtype=np.float64) scaler = MinMaxScaler(feature_range=(1, 3)) # 指定区间范围 print(scaler.fit_transform(X)) print(scaler.data_max_) print(scaler.data_min_) print(scaler.data_range_) # 计算公式 X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0)) print(X_std) #X_scaled = X_std * (max - min) + min X_scaled = X_std * (5 - 1) + 1 print(X_scaled) X_scaled[np.isnan(X_scaled)]=1. print(X_scaled)
[[2. 1. 3. 1. ]
[3. 2. 1.66666667 1. ]
[1. 3. 1. 1. ]]
[2. 1. 2. 3.]
[ 0. -1. -1. 3.]
[2. 2. 3. 0.]
[ [0.5 0. 1. nan]
[1. 0.5 0.33333333 nan]
[0. 1. 0. nan]]
[ [3. 1. 5. nan]
[5. 3. 2.33333333 nan]
[1. 5. 1. nan]]
[ [3. 1. 5. 1. ]
[5. 3. 2.33333333 1. ]
[1. 5. 1. 1. ]]
七、归一化
另一种数据预处理的方式是将特征取值范围归一化到某个区间(scaling),即将样本数据取值限定在特定范围,如[0,1],可用类MinMaxScaler实现;或 MaxAbsScaler将特征取值缩放到[-1,1]。
作用:
– 对非常小的标准偏差的特征更鲁棒
– 在稀疏数据中保留零条目
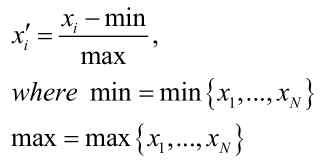
import numpy as np from sklearn.preprocessing import Normalizer X = np.array([ [1, -1, 2], [2, 0, 0], [0, 1, -1] ], dtype=np.float64) normalizer1 = Normalizer(norm='max') # 每个值除以最大值 normalizer2 = Normalizer(norm='l2') # 每个值l2正则 normalizer3 = Normalizer(norm='l1') # 每个值l1正则 normalizer1.fit(X) normalizer2.fit(X) normalizer3.fit(X) print (normalizer1.transform(X)) print ("----------------------------------") print (normalizer2.transform(X)) print ("----------------------------------") print (normalizer3.transform(X)) print(1/np.sqrt(6)) print(1/np.sqrt((X[0]**2).sum())) # 对应原始除以对应正则因子,1/np.sqrt((X[0]**2.sum()))
[[ 0.5 -0.5 1. ]
[ 1. 0. 0. ]
[ 0. 1. -1. ]]
----------------------------------
[[ 0.40824829 -0.40824829 0.81649658]
[ 1. 0. 0. ]
[ 0. 0.70710678 -0.70710678]]
----------------------------------
[[ 0.25 -0.25 0.5 ]
[ 1. 0. 0. ]
[ 0. 0.5 -0.5 ]]
0.4082482904638631
0.4082482904638631
八、多项式转换
import numpy as np from sklearn.preprocessing import PolynomialFeatures X = np.arange(6).reshape(3,2) print(X) poly1 = PolynomialFeatures(2) # 2表示2次方,(x_1 + x_2)^2 poly1.fit(X) print(poly1) print(poly1.transform(X)) #X 的特征已经从 (X_1, X_2) 转换为 (1, X_1, X_2, X_1^2, X_1X_2, X_2^2) poly2 = PolynomialFeatures(interaction_only=True) # 去掉平方项 poly2.fit(X) print(poly2) print(poly2.transform(X)) #X 的特征已经从 (X_1, X_2) 转换为 (1, X_1, X_2,X_1X_2) poly3 = PolynomialFeatures(include_bias=False) # 去掉截距项,即第一列 poly3.fit(X) print(poly3) print(poly3.transform(X))
[[0 1]
[2 3]
[4 5]]
PolynomialFeatures(degree=2, include_bias=True, interaction_only=False)
[[ 1. 0. 1. 0. 0. 1.]
[ 1. 2. 3. 4. 6. 9.]
[ 1. 4. 5. 16. 20. 25.]]
PolynomialFeatures(degree=2, include_bias=True, interaction_only=True)
[[ 1. 0. 1. 0.]
[ 1. 2. 3. 6.]
[ 1. 4. 5. 20.]]
PolynomialFeatures(degree=2, include_bias=False, interaction_only=False)
[[ 0. 1. 0. 0. 1.]
[ 2. 3. 4. 6. 9.]
[ 4. 5. 16. 20. 25.]]
九、特征选择
import numpy as np from sklearn.feature_selection import VarianceThreshold,SelectKBest # VarianceThreshold:异常方差较低的特征,SelectKBest:选择最好的特征 from sklearn.feature_selection import chi2 # 卡方验证 X = np.array([ [0, 2, 0, 3], [0, 1, 4, 3], [0.1, 1, 1, 3] ], dtype=np.float64) Y = np.array([1,2,1]) print(X.std(axis=0)) variance = VarianceThreshold(threshold=0.1) ##设置方差的阈值为0.1 print(variance) variance.fit(X) print(variance.transform(X)) #选择方差大于0.1的特征 sk2 = SelectKBest(chi2, k=2) #选择相关性最高的前2个特征 sk2.fit(X, Y) print(sk2) print(sk2.scores_) print(sk2.transform(X))
[0.04714045 0.47140452 1.69967317 0. ]
VarianceThreshold(threshold=0.1)
[[2. 0.]
[1. 4.]
[1. 1.]]
SelectKBest(k=2, score_func=<function chi2 at 0x000001775F143BF8>)
[0.05 0.125 4.9 0. ]
[[2. 0.]
[1. 4.]
[1. 1.]]
十、异常数据处理
import numpy as np import matplotlib as mpl import pandas as pd import matplotlib.pyplot as plt from sklearn.tree import DecisionTreeRegressor from sklearn.ensemble import BaggingRegressor # 防止中文乱码 mpl.rcParams['font.sans-serif'] = [u'simHei'] mpl.rcParams['axes.unicode_minus'] = False # 设置在jupyter中matplotlib的显示情况 # %matplotlib tk ## 文件存储路径 path1 = "C0904.csv" path2 = "C0911.csv" filename = "X12CO2" # 列的名字 # subplots与figure函数参数解释说明以及简单的使用脚本实例 # https://blog.csdn.net/henni_719/article/details/77479912 ### 原始数据读取 plt.figure(figsize=(10, 6), facecolor='w') # figsize:每英寸的宽度和高度,facecolor:背景色, 此处白色。如果不提供,默认值:figure.facecolor。 plt.subplot(121) # 分成1x2(一行二列),占用第一个,即第一行第一列的子图 data = pd.read_csv(path1, header=0) # 读取数据 x = data[filename].values # 取X12CO2列的值 plt.plot(x, 'r-', lw=1, label=u'C0904') # x:传入y轴的值,r-:红色,lw:线宽, label:线的标签名 plt.title(u'实际数据0904', fontsize=18) # 表格的标题,fontsize:字体大小 plt.legend(loc='upper right') # loc:图的位置,右上 plt.xlim(0, 80000) # x坐标最大值和最小值 plt.grid(b=True) # 是否显示网格 plt.subplot(122) # 分成1x2(一行二列),占用第二个,即第一行第二列的子图 data = pd.read_csv(path2, header=0) x = data[filename].values plt.plot(x, 'r-', lw=1, label=u'C0911') plt.title(u'实际数据0911', fontsize=18) plt.legend(loc='upper right') plt.xlim(0, 80000) plt.grid(b=True) plt.tight_layout(2, rect=(0, 0, 1, 0.95)) #2:图边和子图边的距离,rect: 将其设置为一个矩形,默认(0,0,1,1) plt.suptitle(u'如何找到下图中的异常值', fontsize=20) plt.show() ### 异常数据处理 data = pd.read_csv(path2, header=0) x = data[filename].values width = 300 delta = 5 eps = 0.02 N = len(x) p = [] # 异常值存储 abnormal = [] for i in np.arange(0, N, delta): # [0,5,10,...] s = x[i:i+width] ## 获取max-min的差值 min_s = np.min(s) ptp = np.ptp(s) # 求最大值和最小值的差 ptp_min = ptp / min_s p.append(ptp_min) ## 如果差值大于给定的阈值认为是存在异常值的区间 if ptp_min > eps: abnormal.append(range(i, i+width)) ## 获得异常的数据x值 abnormal = np.array(abnormal) # 将列表转换为Arrray对象 abnormal = abnormal.flatten() # 把数组降到一维 abnormal = np.unique(abnormal) # 去重 #plt.plot(p, lw=1) #plt.grid(b=True) #plt.show() plt.figure(figsize=(18, 7), facecolor='w') plt.subplot(131) plt.plot(x, 'r-', lw=1, label=u'原始数据') plt.title(u'实际数据', fontsize=18) plt.legend(loc='upper right') plt.xlim(0, 80000) plt.grid(b=True) plt.subplot(132) t = np.arange(N) # X的长度 plt.plot(t, x, 'r-', lw=1, label=u'原始数据') # t为x值的序列,x为y值的序列 plt.plot(abnormal, x[abnormal], 'go', markeredgecolor='g', ms=3, label=u'异常值') # g:表示为绿色,go:绿色圆圈 plt.legend(loc='upper right') plt.title(u'异常数据检测', fontsize=18) plt.xlim(0, 80000) plt.grid(b=True) # 预测 plt.subplot(133) select = np.ones(N, dtype=np.bool) # N是形状 select[abnormal] = False print(select) t = np.arange(N) ## 决策树 dtr = DecisionTreeRegressor(criterion='mse', max_depth=10) # criterion是决策树模型,max_depth是深度 br = BaggingRegressor(dtr, n_estimators=10, max_samples=0.3) # 把树模型丢到 集成学习器中,n_estimators:10个弱学习器,max_samples: 每个弱学习器选择30%的样本训练 ## 模型训练 #我们不知道t的shape属性是多少, #但是想让t变成只有一列,行数不知道多少, #通过`t.reshape(-1,1)`,Numpy自动计算出行数 br.fit(t[select].reshape(-1, 1), x[select]) ## 模型预测得出结果 y = br.predict(np.arange(N).reshape(-1, 1)) y[select] = x[select] plt.plot(x, 'g--', lw=1, label=u'原始值') # 原始值 plt.plot(y, 'r-', lw=1, label=u'校正值') # 校正值 plt.legend(loc='upper right') plt.title(u'异常值校正', fontsize=18) plt.xlim(0, 80000) plt.grid(b=True) plt.tight_layout(1.5, rect=(0, 0, 1, 0.95)) plt.suptitle(u'异常值检测与校正', fontsize=22) plt.show()





