快速排序精讲

快速排序是对于冒泡排序的改进

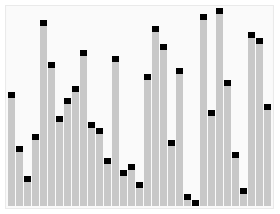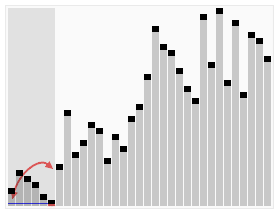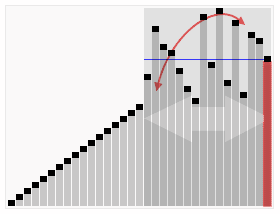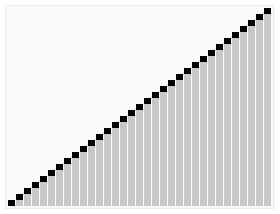
那么它是如何改进的呢？？
假设有n个记录值，冒泡排序的排序过程的最差情况经历n-1趟排序，每一趟排序中
前后相邻的值进行交换，每个值逐步地移动到它应该有的位置，序列从无序状态到渐进到有序状态（每次交换都是相邻交换），经过n-1趟交换效果的累积，终于达到整体有序
相比之下快速排序呢是粗精度到高精度的冒泡排序，首先选取一个PivoKey，用以将序列分成相邻的2段，左边为小值，右边为大值，然后分别对左右部分递归地进行快排，从大范围缩小到小范围，通过较大的跨步，来逐渐靠近所应该在的位置。
（假设其原来在左边，应该的位置在右边，通过快排可以一下子交换过来到右边，而冒泡只能一步步前后交换来到右边，相比之下，大步伐比小步伐走得当然要快）

算法的大致思路：
1.设置PivotKey，同时设置low和high指针,low为最前面元素指针，high为后面元素指针，PivotKey一般为方便取最前面元素L->r[0]=L->r[low]。

那么我可不可以不取L->r[0]而随意取一个数值呢?可以的，只不过稍微比较麻烦一点，详情请见后面解析

2.通过high–不断往前面查找，直到找到某个元素小于PivotKey
将L->r[high]赋值L->r[low]。（此处不会覆盖原有的L->r[low]值，
因为L- >r[low]=PivotKey得到保留。赋值完后L->r[high]=L->r[low]，按道理我们可以将PivoKey赋值给L->r[high]，达到交换值的效果。但是我们的目标是找到PivoKey的位置，并且给这个位置赋值PivoKey，如果此处赋值的话L->r[high]又会被第三步中的赋值覆盖掉，导致此处赋值多余）
3.通过low++，不断往后面查找，直到有某个元素大于PivotKey，
L->r[low]赋值L->r[high]（此处L->r[high]其实多余，因为在上一步中已经移走，所以将L->r[low]赋值L->r[high]不会因为覆盖而丢失值）
4.重复上述第2步至第3步，直到low=high，返回low值。
（通过不断的比较逼近找到PivotKey值的位置，当low=high时，这个位置就是此Pivot值在最后序列中的位置）
5.通过以上步骤，无序序列已经分为以PivoKey为界，左小右大的两部分。接下来对左右两部分递归执行上述1~4步

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 30
typedef struct{
     int  r[MAXSIZE];
     int length;
}SqList;

int  Partition(SqList *L,int low,int high){
       int  Pivokey=L->r[low];
       while(low<high){
            while(low<high&&L->r[high]>=Pivokey）
                  --high;//当Pivokey，为最小值时high--可能指针越界，所以需要设置low<high
            L->r[low]=L->r[high];
            while(low<high&&L->r[low]<=Pivokey)
                  ++low;//当Pivokey，为最小值时low++可能指针越界，所以需要设置low<high
            L->r[high]=L->r[low];
       }
       L->r[low]=Pivokey;//确定位置后赋值PivotKey
       return  low;//返回位置
}

void QSort(SqList *L,int low,int high){
     if(low<high){
        int mid=Partition(L,low,high);
        if(mid!=low) //如果刚好是最小值，就会mid=low，此时无需再比较左端
           QSort(L,low,mid-1);
        if(mid!=high)//如果刚好是最大值，就会mid=high，此时无需再比较右端
           QSort(L,mid+1,high);
     }
     return;
}

void QuickSort(SqList *L){
     QSort(L,0,L->length-1);
     return;
}

int main()
{
    SqList L;
    L.length=12;
    for(int i=0;i<12;i++)
        scanf("%d",&L.r[i]);
    printf("Befor Sort:\n");
    for(int i=0;i<12;i++)
        printf("%d\t",L.r[i]);
    QuickSort(&L);
    printf("\nAfter Sort:\n");
    for(int i=0;i<12;i++)
        printf("%d\t",L.r[i]);
    return 0;
    return 0;
}

那么回到之前留下的一个问题：
如果随意取一个数组元素值该怎么样呢？？
假如赋值L->r[4]赋值给PivotKey，则仍然是从high–找小于PivotKey值，只不过当找到以后L->r[high]不能赋值给L->r[low],而是首先赋值给L->r[4],因为之前L->r[4]赋值给PivotKey，值得以保留，如果赋值给L->r[low]，则会出现L->r[low]原值被覆盖丢失
接下来的步骤便与之前相同，从low++寻找到大于PivotKey的值后赋值给L->r[high],因为原来的L->r[high]赋值给了L->r[4]得以保留。