小波变换的引入，通俗易懂

很多通信工程学生，几乎每天接触时频变换，但通常不知道为什么要时频变换、变换之间的关系，变换产生的图代表什么意义，基于这些问题，我尝试做下梳理：

1、为什么要进行时频变换？

（1）在频率域能看到很多时域无法直接看到的现象，比如频率分布；

　　对于确定的信号其时域表示是确定的，我们可以通过傅里叶变换得到其确定的频谱分布；

　　对于随机信号不能用确定的时间函数表示，我们要想对其探索，只能选取合适的时频变换方式，比如小波变换、S变换等时频分析方法，通过时频转换，我们可以透过时频分布图很清晰的看到，随机信号的主要合成信号是哪些，以及主要信号所对应的频率，产生的时间。

2、变换之间的关系

首先看下傅里叶变换：

缺点：对非*稳信号，傅里叶变换有局限性！看如下一个简单信号的傅里叶变换

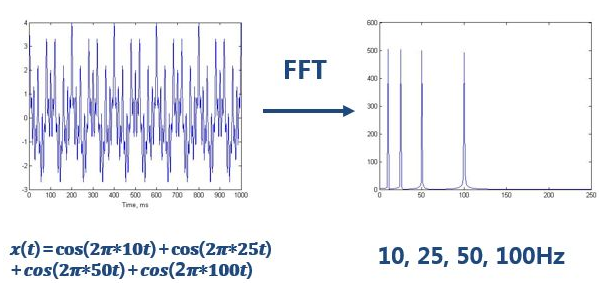
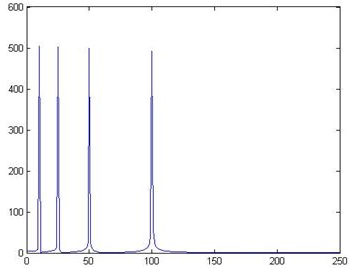
做完FFT（快速傅里叶变换）后，可以在频谱上看到清晰的四条线，信号包含四个频率成分。

一切没问题。但是，如果是频率随着时间变化的非*稳信号呢？

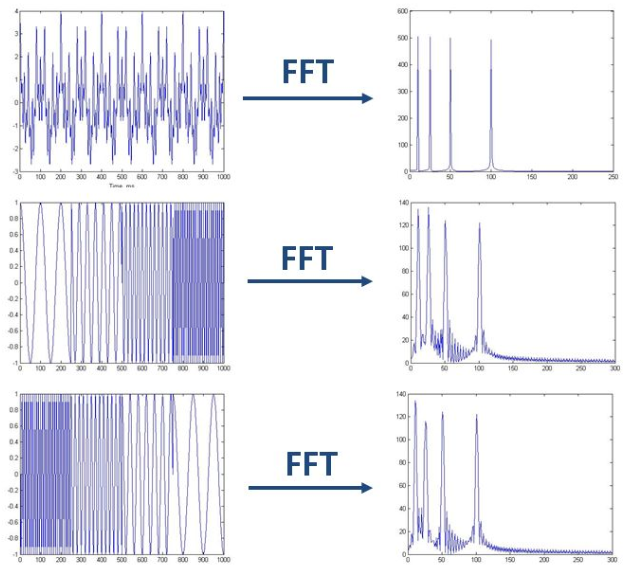
如上图，最上边的是频率始终不变的*稳信号。而下边两个则是频率随着时间改变的非*稳信号，他们同样包含和最上边信号相同频率的四个成分。做完FFT后，我们发现这三个时域上有巨大差异的信号，频谱（幅值谱）却非常一致。尤其是下边两个非*稳信号，我们从频谱上无法区分他们，因为他们包含的四个频率的信号的成分确实是一样的，只是出现的先后顺序不同。

可见，傅里叶变换处理非*稳信号有天生的缺陷。它只能获取一段信号总体上包含哪些频率成分，但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号，可能频谱图一样。

然而，*稳信号大多是人为制造出来的，自然界的大量信号几乎都是非*稳的，所以在比如生物医学信号分析等领域中，基本看不到单纯的傅里叶变换这样的方法

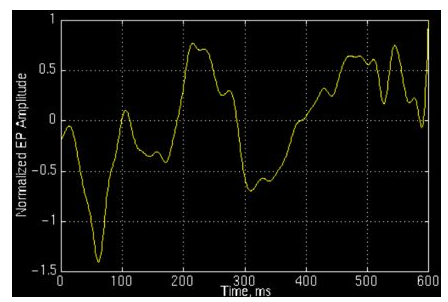
上图所示的是一个正常人的相关电位。对于这样的非*稳信号，只知道包含哪些频率成分是不够的，我们还想知道各个成分出现的时间，知道信号频率随时间变换的情况，各个时刻的瞬时频率及其幅值——这也就是时频分析

 二、短时傅里叶变换（STFT）

一个简单可行的方法就是——加窗。把整个时域过程分解成无数个等长的小过程，每个小过程*似*稳，再傅里叶变换，就知道在哪个时间点上出现了什么频率了。这就是短时傅里叶变换。

如下图所示：

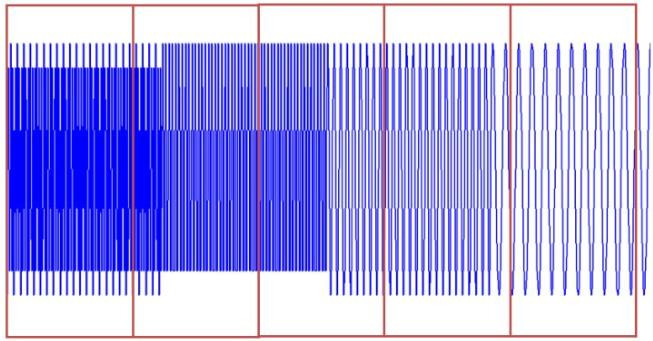
时域上分成一段一段做FFT，不就知道频率成分随时间的变化情况了吗！

用这样的方法，就可以得到一个信号的时频图了：

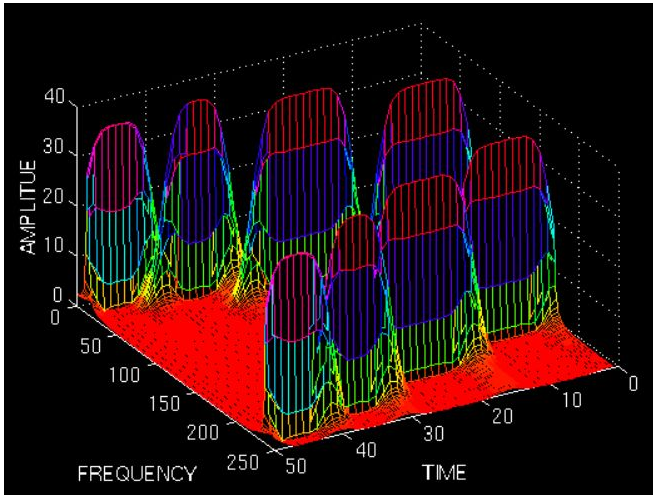
图上既能看到10Hz，25Hz，50Hz，100Hz四个频域成分，还能看到出现的时间，两排锋是对称的，所以大家只看一排就行了。

时频分析结果到手了，但是STFT依然有缺陷。

 问题一，我们应该用多宽的窗函数？窗 太宽太窄都有问题

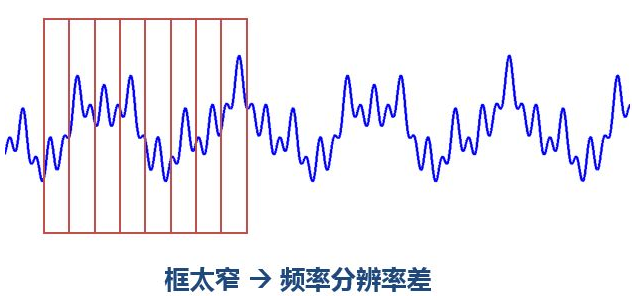
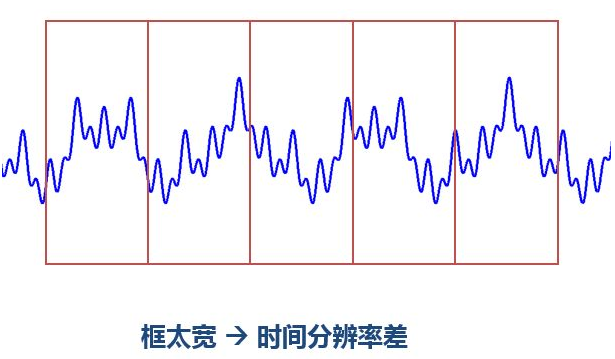
窗太窄，窗内的信号太短，会导致频率分析不够精准，频率分辨率差。窗太宽，时域上又不够精细，时间分辨率低。（这个道理可以用海森堡不确定性原理来解释。类似于我们不能同时获取一个粒子的动量和位置，我们也不能同时获取信号绝对精准的时刻和频率。这也是一对不可兼得的矛盾体。我们不知道在某个瞬间哪个频率分量存在，我们知道的只能是在同一个时间段内某个频带的分量存在。所以绝对意义的瞬时频率是不存在的）

看看实例效果吧：

 

 

 

 

 

 

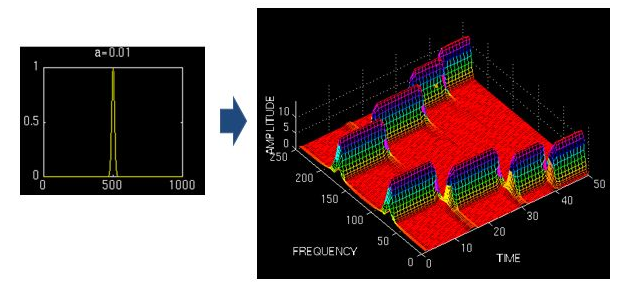
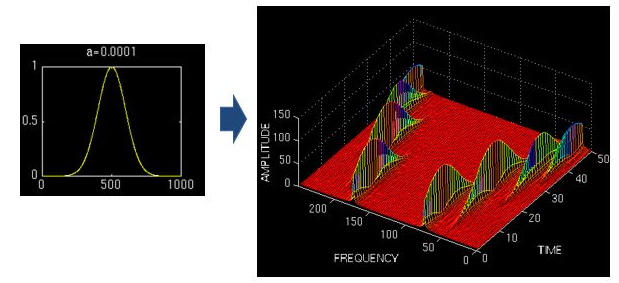
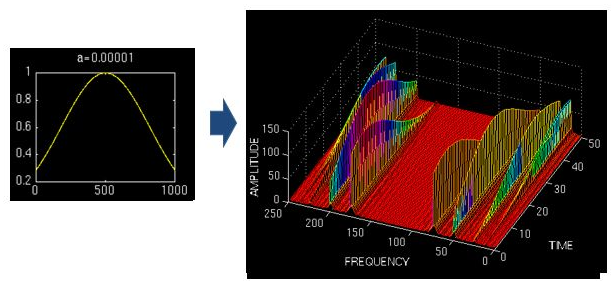
 上图是对同一个信号（4个频率成分）采用不同宽度的窗做成的STFT，结果如右图，时频图在时间轴上的分辨率很高，几个锋基本成矩形，而用宽窗则变成了绵延的矮山。但是频率轴上，窄窗明显不如下边两个宽窗精确

所以窄窗口时间分辨率高、频率分辨率低，宽窗口时间分辨率低，频率分辨率高。对于时变的非稳态信号，高频适合小窗口，低频适合大窗口。然而STFT的窗口是固定的，在一次STFT中宽度不会变化，所以STFT还是无法满足非稳态信号变化的频率需求。

三、小波变换

那么你可能会想到，让窗口大小变起来，多做几次STFT不就可以了吗?没错，小波变换就有这样的思路。

但事实上小波并不是这么做的，小波变换就是根据算法，加不等长的窗，对每一小部分进行傅里叶变换的话就不准确了。小波变换并没有采用窗的思想，更没有做傅里叶变换

至于为什么不采用可变窗的STFT呢，我认为是因为这样做冗余太严重，STFT做不到正交化，这也是它的一大缺陷。

 于是小波变换的出发点和STFT还是不同的。STFT是给信号加窗，分段做FFT；而小波变换直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获得频率，还可以定位到时间了

 解释：

傅里叶变换把无限长的三角函数作为基函数（我们通常学的信号与系统书就是这样引入的）：

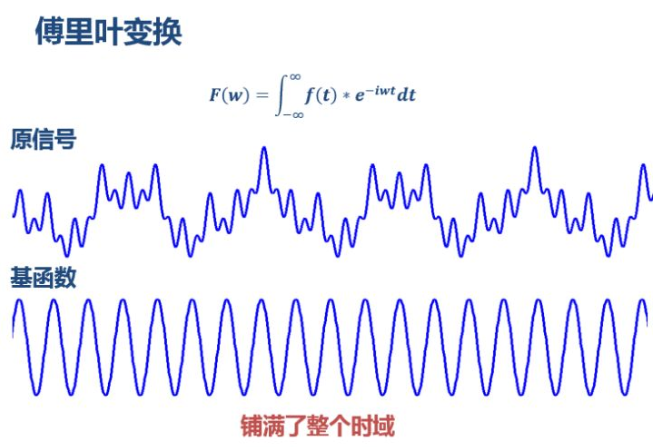
这个基函数会伸缩、会*移（其实本质并非*移，而是两个正交基的分解）。缩的窄，对应高频；伸的宽，对应低频。然后这个基函数不断和信号做相乘。某一个尺度（宽窄）下乘出来的结果，就可以理解成信号所包含的当前尺度对应频率成分有多少。于是，基函数会在某些尺度下，与信号相乘得到一个很大的值，因为此时二者有一种重合关系。那么我们就知道信号包含该频率成分的多少。

仔细体会下可以发现，这一步其实是在计算信号和三角函数的相关性

 

 

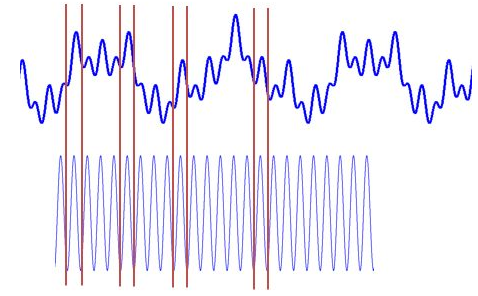
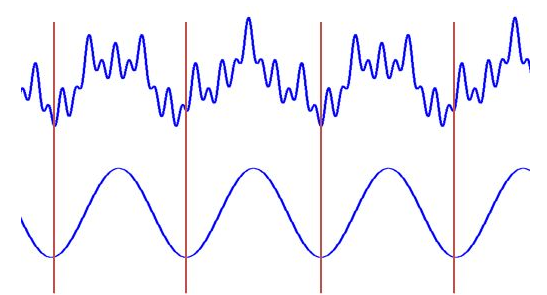
这两种尺度能相乘出一个大的值，所以信号包含较多的两个频率成分，在频谱上这两个频率会出现两个锋

以上，就是粗浅意义上的傅里叶变换原理。

如前边所说，小波变换的改变就在于，将无限长的三角函数基换成了有限长的会衰减的小波基

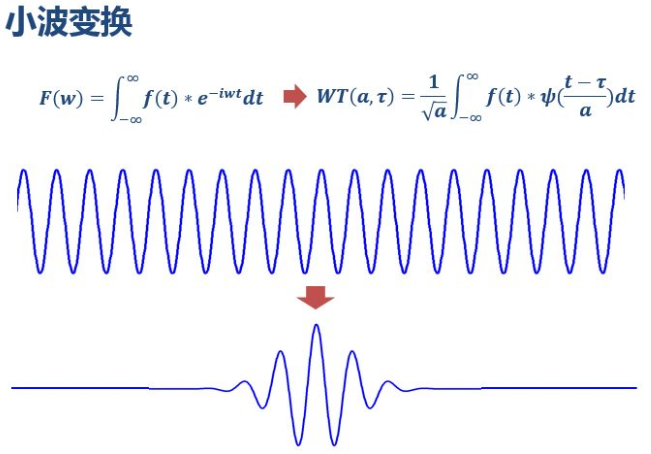
这就是为什么他叫“小波”，因为是一个很小的波嘛~

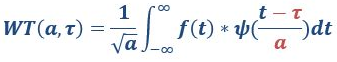
从公式可以看出，不同于傅里叶变换，变量只有频率w，小波变换有两个变量：尺度a（scale）和*移量 ζ（translation）。尺度a控制小波函数的伸缩，*移量 ζ控制小波函数的*移。尺度就对应于频率（反比），*移量ζ就对应于时间。

 

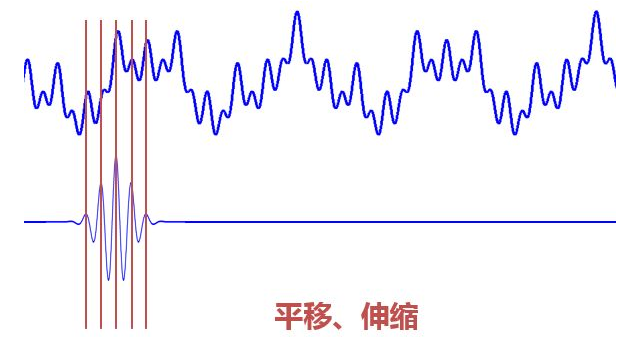
当伸缩、*移到这么一种重合情况时，也会相乘得到一个大的值。这时候和傅里叶变换不同的是，这不仅可以知道信号有这样频率的成分，而且知道它在时域上存在的具体位置。

 而当我们在每个尺度线都*移着和信号乘过一遍后，我们就知道信号在每个位置上都包含哪些频率成分

看到了吗？有了小波，我们从此再不害怕非稳定信号啦！从此可以做时频分析啦！

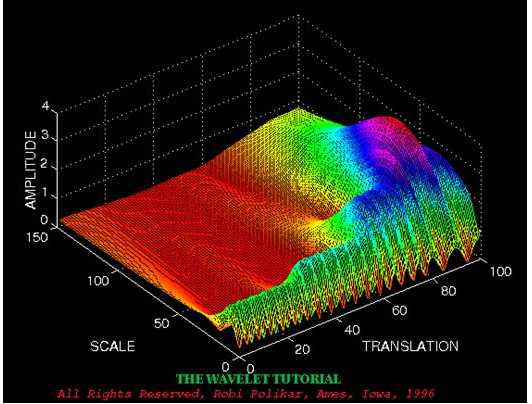
做傅里叶变换只能得到一个频谱，做小波变换却可以得到一个时频谱

时域信号

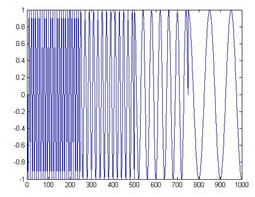
 傅里叶变换结果

 

小波变换结果

小波变换还有一些好处，比如，我们知道对于突变信号，傅里叶变换存在吉布斯效应，我们用无限长的三角函数怎么也拟合不好突变信号：

 

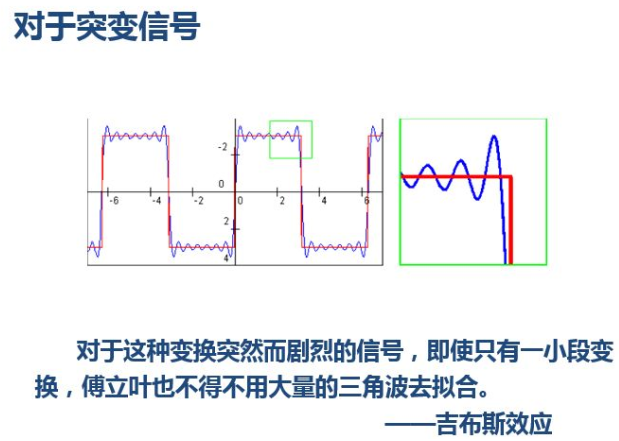
 然而衰减的小波就不一样了：

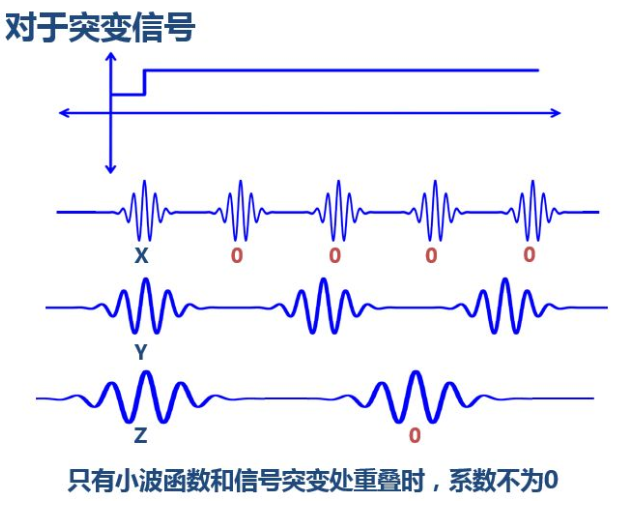
以上，就是小波的意义。

问题一、海森堡不确定性原理：

不确定性原理，或者叫做测不准原理，最早出自量子力学，意为在微观世界，离子的位置与动量不可同时被确定。但是这个原理并不局限于量子力学，有很多物理量都有这样的特征，比如能量和时间、角动量和角度。体现在信号领域就是时域和频域。不过更准确一点的表述应该是：一个信号不能再时空域和频域上同时过于集中；一个函数时域窄，它经过傅里叶变换的频域后就越宽。

问题二、关于正交化

什么是正交化？为什么说小波能实现正交化是优势？

简单说，如果采用正交基，变换域系数会没有冗余信息，变换前后的信号能量相等，等于是用最少的数据表达最大的信息量，利用数值压缩等领域。

问题三、关于瞬时频率，图中时刻点对应一频率值，一个时刻点只有一个信号值，又怎么能得到他的频率呢？

很好的问题。如文中所说，绝对意义的瞬时频率其实是不存在的，但看一个时刻点的一个信号值，当然得不到他的频率。我们只不过是很短的一段信号的频率作为该时刻表的频率，所以我们得到的只是时间分辨率有限的*似分析结果。这一想法在STFT上体现的很明显，小波用衰减的基函数去测定信号的瞬时频率，思想也类似

总结：
傅里叶变换：知道一段时间内，信号各个频率分量分别多少

小波变换：知道一段时间内，信号的各个频率分量分别是多少，以及他们都是什么时候出现的