数据结构-查找
查找:查找就是根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素(或记录)。
动态查找表:在查找过程中同时插入 查找表中不存在的数据元素,或者从查找表中删除已经存在的某个数据元素。
顺序查找:又叫线性查找,是最基本的查找技术,他的查找过程是:从表中第一个(或最后一个)记录开始,逐个进行记录的关键字和给定比值比较,若某个记录的关键字和给定值相等,则查找成功,找到所查找的记录;如果直到最后一个(或第一个)记录,其关键字和给定值比价都不等时,则表中没有所查的记录,查找不成功。
很显然,顺序查找技术有很大缺点的,n很大时,查找效率极为低下,不过优点也是有的,这个算法非常简单,对静态查找表的记录没有任何要求,在一些小型数据的查找时,是可适用的。
另外,也正由于查找概率的不同,我们完全可以把容易查找到的记录放在前面,而不常用的记录放在后面,效率就可以大幅提高。
折半查找:又称二分查找。他的前提是线性表中的记录必须是关键码的有序(通常从小到大有序),线性表必须采用顺序存储。折半查找的基本思想是:在有序表中,取中间记录作为比较对象,若给定值与中间记录的关键字相等,则查找成功;若给定值小于中间记录的关键字,则中间记录的左半区继续查找;若给定值大于中间记录的关键字,则在中间记录的右半区继续查找。不断重复上述过程,直到查找成功,或所有查找区域无记录,查找失败为止。
由于折半查找的前提条件是需要有序表顺序存储,对于静态查找表,依次排序后不再变换,这样的算法已经比较好了,但对于需要频繁执行插入和删除操作的数据集来说 ,维护有序的排序会带来不小的工作量,那就不建议使用。
插值查找是根据要查找的关键字key与查找表中最大最小记录的关键字比较后的查找方法,其核心就在于插值的计算公式(key-a[low])/(a[high]-a[low]).应该说,从时间复杂度来看,他也是O(logn),但对于表长较大,而关键字分布又比较均匀的查找表来说,插值查找算法的平均性能比折半查找要好得多。反之,数组中如果分布类似{0,1,2,2000,2001,…,999998,999999}这种极端不均匀的数据,用插值查找未必是很合适的选择。
斐波那契查找算法的核心在于:
1) 当key=a[mid]时,查找就成功;
2) 当key<a[mid]时,新范围时第low个到第mid-1个,此时范围个数为F[k-1]-1个;
3) 当key>a[mid]时,新范围是第m+1个到第high个,此时范围个数为F[k-2]-1个;如下图所示:
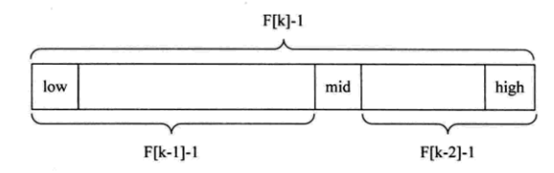
也就是说,如果要查找的记录在右侧,则左侧的数据都不用再判断了,不断反复进行下去,对处于当中的大部分数据,其工作效率要高一些。所以尽管斐波那契查找的时间复杂也为O[logn],但就平均性能来说,斐波那契查找要由于折半查找。可惜如果是最坏情况,比如这里key=1,那么始终都处于左侧长版区在查找,则查找雄安率要低于折半查找。
还有比较关键的一点,折半查找是进行加法与除法运算(mid=(low+high)/2),插值查找进行复杂的四则运算(mid=low+(high-low)*(key-a[low])/(a[high]-a[low])),而斐波那契查找只是最简单加减法运算(mid=low+F[k-1]-1),在海量数据的查找过程中,这种细微的差别可能会影响最终的查找效率。
应该说,三种有序表的查找本质上是分割点的选择不同,各有优劣,实际开发时,可根据数据的特点综合考虑再做出选择。
能够快速查找到需要的数据的办法就是索引
索引就是把一个关键字与它对应的记录相关联的过程,一个索引由若干个索引项构成,每个所印象至少应包含关键字和其对应的记录在存储器中的位置等信息。索引技术是组织大型数据库以及磁盘文件的一种重要技术
所谓线性索引就是将索引项集合组织为线性结构,也称为索引表。
稠密索引是指在线性索引中,将数据集中的每个记录对应一个索引项,对于稠密索引这个索引表来说,索引项一定是按照关键码有序的排列。索引项有序也就意味着,我们要查找关键字时,可以用到折半、插值、斐波那契等有序查找算法,大大提高了效率。
稠密索引因为索引项与数据集的记录个数相同,所以空间代价很大。为了减少索引项的个数,我们可以对数据集进行分块,使其分块有序,然后再对每一块建立一个索引项,从而减少索引项的个数。
分块有序,是把数据集的记录分成了若干块,并且这些块需要满足两个条件:
块内无序:即每一块内的记录不要求有序。
块间有序。
总的来说,分块索引在兼顾了对细分块不需要有序的情况下,大大增加了整体查找的速度,所以普遍被用于数据库表查找等技术的应用当中。
二叉排序树,又称二叉查找树。他或者是一颗空树,或者是具有下列性质的二叉树。
1、 若它的左子树不空,则左子树上所有结点的值均小于它的跟结构的值
2、 若它的右子树不空,则右子树上所有结点的值均大于他的根节点的值;
3、 他的左右子树也分别是二叉排序树。
它的结点满足一定的次序关系,左子树结点一定比其双亲结点小,右子树结点一定比其双亲结点大。
构造一颗二叉排序树的目的,其实并不是为了排序,而是为了提高查找和插入删除的关键字的速度。
总之,二叉排序树是以链接的方式存储,保持了链接存储结构在执行插入或删除操作时不用移动元素的有点,只要找到合适的插入和删除位置后,仅需修改链接指针即可。插入删除的时间性能比较好。而对于二叉排序树的查找,走的就是从根节点到要查找的结点的路径,其比较次数等于给定值的结点在二叉排序树的层数,极端情况,最少为1次,即根节点就是要找的结点,最多也不会超过树的深度。也就是说,二叉排序树的查找性能取决于二叉排序树的形状。
平衡二叉树是一种二叉排序树,其中每一个结点的左子树和右子树的高度差之多等于1.我们将二叉树上的结点左子树的深度减去右子树的深度的值叫做平衡因子BF,那么平衡因子只可能是-1、0、1.
距离插入结点最近的,且平衡因子的绝对值大于1的结点为根的子树,我们称之为最小不平衡子树。
散列表:
散列技术是在记录的存储位置和它的关键字之间建立一个不确定的对应关系f,使得每个关键字key对应一个存储位置f(key)。查找时,根据这个确定的对应关系找到给定值key的映射f(key),若查找几何中存在这个记录,则必定在f(key)的位置上。
我们把这种对应关系f称为散列函数,又称为哈希函数。按这个思想,采用散列技术将记录存储在一块连续的存储空间中,这块连续存储空间称为散列表或哈希表。
整个散列过程其实就是两步:
1、 在存储时,通过散列函数计算记录的散列地址,并按此散列地址存储该记录。
2、 当查找记录时,我们通过同样的散列函数计算记录的散列地址,按此散列地址访问该记录。
散列技术最适合的求解问题是查找与给定值相等的记录。
总结回顾:
首先我们要弄清楚查找表、记录、关键字、主关键字、静态查找表、动态查找表等这些概念。
然后,对于顺序查找来说,尽管很土(简单),但它却是后面很多查找的基础,注意设置“哨兵”的技巧,可以使得本已经很难提升的简单算法里还是提高了性能。
有序查找,我们着重讲了折半查找的思想,他在性能上比原来的顺序查找有了质地飞跃,由O[n]变成了O[logn]。之后我们又讲解了另外两种优秀的有序查找:插值查找和斐波那契查找,三者各有优缺点。
线性索引查找,我们讲解了稠密索引、分块索引和倒排索引。索引技术被广泛的用于文件检索、数据库和搜索引擎等技术领域,是进一步学习这些技术的基础
二叉排序树是动态查找最重要的数据结构,它可以在兼顾查找性能的基础上,让插入和删除也变得效率较高,不过为了达到最优的状态,二叉排序树最好是构造称平衡的二叉树才最佳。因此我们就需要再学习关于平衡二叉树(AVL树)的数据结构,
B树这种数据结构是针对内存与外存之间的存取而专门设计的。由于内外存的查找性能更多取决于读取的次数,因此在设计中要考虑B树的平衡和层次。我们讲解时是先通过最简单的B树(2-3树)来理解如何构建、插入、删除元素的操作,再通过2-3-4树的神话,最终来理解B树的原理。
散列表是一种非常高效的查找数据结构,在原理上也与前面的查找相同,它回避了关键字之间反复比较的繁琐,而是直接一步到尾查找结果。当然,这也就带来了记录之间没有任何关联的弊端。应该说,散列表对于那种查找性能要求高,记录之间关系无要求的数据有非常好的适用性。在学习中要注意的是散列函数的选择和处理冲突的方法。



