TensorFlow-实战Google深度学习框架 笔记(上)
TensorFlow
TensorFlow 是一种采用数据流图(data flow graphs),用于数值计算的开源软件库。在 Tensorflow 中,所有不同的变量和运算都是储存在计算图,所以在我们构建完模型所需要的图之后,还需要打开一个会话(Session)来运行整个计算图
通常使用import tensorflow as tf来载入TensorFlow
在TensorFlow程序中,系统会自动维护一个默认的计算图,通过tf.get_default_graph函数可以获取当前默认的计算图。除了使用默认的计算图,可以使用tf.Graph函数来生成新的计算图,不同计算图上的张量和运算不会共享
在TensorFlow程序中,所有数据都通过张量的形式表示,张量可以简单的理解为多维数组,而张量在TensorFlow中的实现并不是直接采用数组的形式,它只是对TensorFlow中运算结果的引用。即在张量中没有真正保存数字,而是如何得到这些数字的计算过程
如果对变量进行赋值的时候不指定类型,TensorFlow会给出默认的类型,同时在进行运算的时候,不会进行自动类型转换
会话(session)拥有并管理TensorFlow程序运行时的所有资源,所有计算完成之后需要关闭会话来帮助系统回收资源,否则可能会出现资源泄漏问题
一个简单的计算过程:
import tensorflow as tf
a = tf.constant([1, 2], name='a')
b = tf.constant([3, 4], name='b')
c = a + b
with tf.Session() as sess:
print(sess.run(c))
可以通过ConfigProto Protocol Buffer来配置需要生成的会话:
config = tf.ConfigProto(allow_soft_placement=True, log_device_placement=True)
sess1 = tf.InteractiveSession(config=config)
sess2 = tf.Session(config=config)
通过ConfigProto可以配置类似并行的线程数、GPU分配策略、运算超时时间等参数。当allow_soft_placement设置为True时,当出现以下情况,GPU上的运算可以放到CPU上进行:
- 运算无法在GPU上执行
- 没有GPU资源
- 运算输入包含对CPU计算结果的引用
当log_device_placement设置为True时,日志中将会记录每个节点被安排在哪个设备上以方便调试
使用神经网络解决分类问题主要分为以下4个步骤:
- 提取问题中实体的特征向量作为神经网络的输入
- 定义神经网络的结构,并定义如何从神经网络的输入得到输出
- 通过训练数据来调整神经网络中参数的取值
- 使用训练好的神经网络来预测未知的数据
TensorFlow中矩阵乘法的使用:
tf.matmul(x, w)
tf.random_normal函数可以产生一个矩阵,矩阵中的元素是均值为0,标准差为指定数的随机数,TensorFlow中,一个变量在被初始化之前,该变量的初始化过程需要被明确地调用:
a = tf.Variable(tf.random_normal([2, 3], stddev=2))
b = tf.Variable(tf.random_normal([2, 3], stddev=2))
c = tf.matmul(a, b)
with tf.Session() as sess:
sess.run(a.initializer)
sess.run(b.initializer)
print(sess.run(c))
一个简化初始化过程的函数,可以实现初始化所有变量的过程:
init_op = tf.global_variables_initializer()
sess.run(init_op)
通过tf.global_variables()函数可以拿到当前计算图上的所有变量,有助于持久化整个计算图的运行状态
TensorFlow中,变量的类型是不可改变的,而纬度是可以更改的,只是需要设置validate_shape=False
TensorFlow提供了placeholder机制用于提供输入数据。placeholder相当于定义了一个位置,这个位置中的数据在程序运行时再指定。这样在程序中就不需要生成大量常量来提供输入数据,而只需要将数据通过placeholder传入TensorFlow计算图。在placeholder定义时,这个位置的数据类型需要指定,纬度信息可以推导出来,所以不一定要给出
a = tf.Variable(tf.random_normal([2, 3], stddev=2))
x = tf.placeholder(tf.float32, shape=(1, 2), name='input')
v1 = tf.matmul(x, a)
with tf.Session() as sess:
sess.run(a.initializer)
print(sess.run(v1, feed_dict={x : [[6, 7]]}))
在shape的一个纬度上使用None可以方便使用不同的batch大小shape(None, 3)
假定损失函数为loss = (...),一次训练过程为sess.run(loss, feed_dict{x: X, ...})
TensorFlow提供了7种激活函数,其中常用的有:tf.nn.relu,tf.sigmoid,tf.tanh
一个简单的实现两层神经网络的前向传播算法:
a = tf.nn.relu(tf.matmul(x, w1) + biases1)
y = tf.nn.relu(tf.matmul(a, w2) + biases2)
其中biases为偏向
w为了判断一个输出向量和期望的向量的接近程度,可以使用交叉熵
交叉熵公式: 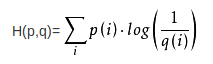
交叉熵定义了两个概率分布之间的距离,即可以表示通过概率分布q来表达概率分布p的困难程度,该值越小说明拟合越好
TensorFlow支持的交叉熵的Demo:
cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, le-10, 1.0)))
其中, y_为正确结果,y为预测值,tf.clip_by_value(y, a, b)将y的值限制在a、b之间,reduce_mean取均值
softmax函数用于将原始网络的输出当作置信度生成新的输出
softmax: 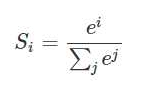
交叉熵一般与softmax回归一起使用
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y)
y表示原始神经网路输出结果,y_给出了标准答案
对于回归问题最常用的损失函数是均方误差(MSE),即方差取均值
TensorFlow支持为:
mse = tf.reduce_mean(tf.square(y_ - y))
tf.greater和tf.where可以用来实现选择操作。tf.greater输入两个张量,比较大小,然后返回比较结果,tf.where输入三个参数,第一个为条件参数,当其为True时,该函数会选择第二个参数的值,否则选择第三个值
v1 = tf.constant([1, 2, 3, 4])
v2 = tf.constant([4, 3, 2, 1])
sess = tf.InteractiveSession()
print(tf.greater(v1, v2).eval()) # [False False True True]
print(tf.where(tf.greater(v1, v2), v1, v2).eval()) # [4 3 3 4]
sess.close()
自定义损失函数的TensorFlow例子:
import tensorflow as tf
from numpy.random import RandomState
batch_size = 8
x = tf.placeholder(tf.float32, shape=(None, 2), name='x-input')
y_ = tf.placeholder(tf.float32, shape=(None, 1), name='y-input')
w1 = tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
y = tf.matmul(x, w1)
# 损失函数,且预测少了的损失更大
loss_less = 10
loss_more = 1
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * loss_more, (y_ - y) * loss_less))
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)
# 生成模拟数据集
rdm = RandomState(1)
dataset_size = 128
X = rdm.rand(dataset_size, 2)
# 设置正确预测的值,并加上 -0.05 ~ 0.05的噪音
Y = [[x1 + x2 + rdm.rand() / 10.0 - 0.05] for (x1, x2) in X]
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS = 5000
for i in range(STEPS):
start = (i * batch_size) % dataset_size
end = min(start + batch_size, dataset_size)
sess.run(train_step, feed_dict={x: X[start: end], y_ : Y[start: end]})
print(sess.run(w1))
梯度下降算法主要用于优化单个参数的取值,而反向传播算法给出了一个高效的方式在所有参数上使用梯度下降算法,从而使神经网络模型在训练数据上的损失函数尽可能小
梯度下降法公式:
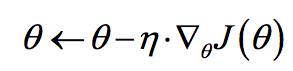
其中n为学习率
梯度下降方法存在的问题有:
- 不一定能得到全局最优解
- 计算时间过长
因为损失函数是所有训练数据上的损失和,所以时间过长,可以使用随机梯度下降算法来加速过程。该算法在每一轮迭代中随机优化某一条训练数据上的损失函数,当然这样可以进行加速,但是存在更大的不能得到最优解的问题
为了折中这两种算法,可以每次计算一小部分训练数据的损失函数,这一小部分称之为一个batch
已知当我们设置学习率的时候,我们应该首先选取一个较大的学习率,然后在训练的过程中逐渐进行衰减。TensorFlow提供了一种灵活的学习率的设置方法--指数衰减法。tf.train.exponential_decay函数实现了指数衰减学习率,其减小的方法为:
decayed_learning_rate = learning_rate * decay_rate ^ (global_step / decay_steps)
decayed_learning_rate为每一轮优化时使用的学习率,learning_rate为事先设定的初始学习率,decay_rate为衰减系数,decay_steps为衰减速度
decay_steps通常代表完整地使用一遍训练数据所需要的迭代轮数,即总样本数除以每一个batch中的训练样本数,如此,就可以每完整的过完一遍训练数据,学习率就减小一次
使用方法:
global_step = tf.Variable(0)
learning_rate = tf.train.exponential_decay(0.1, global_step, 100, 0.96, staircase=True)
learning_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss=loss, global_step=global_step)
0.01为初始学习率,因设置starcase,所以每训练100轮,学习率乘以0.96
当出现过拟合的情况的时候,可以使用正则化的方法来优化,此时不再直接优化
而是优化
其中,
刻画了模型的复杂程度
表示模型复杂损失在总损失中的比例
正则化范式:
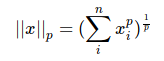
L1正则化会将参数变得更稀疏,而L2不会
TensorFlow对正则化的支持:
loss = tf.reduce_mean(tf.square(y_ - y) + tf.contrib.layers.l2_regularizer(lambda)(w))
TensorFlow会将L2的正则化损失值除以2使得求导得到的结果更简洁
使用滑动平均可以使得模型更具健壮性,TensorFlow提供的方法为tf.train.ExponentialMovingAverage,使用时需要提供一个衰减率,其会维护一个影子变量(shadow variable),其更新方法为:
shadow_variable = decay * shadow_variable + (1 - decay) * variable
其中,decay为衰减率,decay越大,模型越稳定,通常将decay设置为接近1的数,variable为待更新的变量
如果该函数提供了num_updates参数来动态设置decay的大小,那么衰减率将变为:
滑动平均样例:
v1 = tf.Variable(0, dtype=tf.float32)
# step控制衰减率
step = tf.Variable(0, trainable=False)
ema = tf.train.ExponentialMovingAverage(0.99, step)
# 定义一个更新变量滑动平均的操作,每次执行这个操作时,列表中的变量就会被更新
maintain_averages_op = ema.apply([v1])
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
# 通过ema.average(v1)获取滑动平均之后变量的取值
print(sess.run([v1, ema.average(v1)])) # [0.0 0.0]
# 赋值
sess.run(tf.assign(v1, 5))
# 更新v1的滑动取值
sess.run(maintain_averages_op)
print(sess.run([v1, ema.average(v1)])) # [5.0, 4.5]
sess.run(tf.assign(step, 10000))
sess.run(tf.assign(v1, 10))
sess.run(maintain_averages_op)
print(sess.run([v1, ema.average(v1)])) # [10.0, 4.555]
sess.run(maintain_averages_op)
print(sess.run([v1, ema.average(v1)])) # [10.0, 4.60945]
一个mnist数字识别的简单例子,使用TensorFlow完成
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
# mnist = input_data.read_data_sets("/home/fan/dataset/mnist/", one_hot=True)
# print("mnist data info")
# print("Training data size: ", mnist.train.num_examples)
# print("Validating data size: ", mnist.validation.num_examples)
# print("Testing data size: ", mnist.test.num_examples)
# print("Example training data: ", mnist.train.images[0])
# print("Example training data label: ", mnist.train.labels[0])
INPUT_NODE = 784 # 输入层节点数 28 * 28
OUTPUT_NODE = 10 # 区分 0-10
LAYER1_NODE = 500 # 一个有500个节点的隐藏层
BATCH_SIZE = 100 # 一批训练数据个数
LEARNING_RATE_BASE = 0.8
LEARNING_RATE_DECAY = 0.99
REGULARIZATION_RATE = 0.0001 # 正则化项在损失函数中的系数
TRAINING_STEPS = 30000 # 训练轮数
MOVING_AVERAGE_DECAY = 0.99
def inference(input_tensor, avg_class, weights1, biases1, weights2, biases2):
# 当没有提供滑动平均类时,直接使用参数当前的取值
if avg_class is None:
layer1 = tf.nn.relu(tf.matmul(input_tensor, weights1) + biases1)
return tf.matmul(layer1, weights2) + biases2
else:
layer1 = tf.nn.relu(tf.matmul(input_tensor, avg_class.average(weights1)) + avg_class.average(biases1))
return tf.matmul(layer1, avg_class.average(weights2)) + avg_class.average(biases2)
def train(mnist):
x = tf.placeholder(tf.float32, [None, INPUT_NODE], name='x-input')
y_ = tf.placeholder(tf.float32, [None, OUTPUT_NODE], name='y-input')
# 隐藏层参数
weights1 = tf.Variable(tf.truncated_normal([INPUT_NODE, LAYER1_NODE], stddev=0.1))
biases1 = tf.Variable(tf.constant(0.1, shape=[LAYER1_NODE]))
# 输出层参数
weights2 = tf.Variable(tf.truncated_normal([LAYER1_NODE, OUTPUT_NODE], stddev=0.1))
biases2 = tf.Variable(tf.constant(0.1, shape=[OUTPUT_NODE]))
y = inference(x, None, weights1, biases1, weights2, biases2)
global_step = tf.Variable(0, trainable=False)
variable_averages = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY, global_step)
variables_averages_op = variable_averages.apply(tf.trainable_variables())
average_y = inference(x, variable_averages, weights1, biases1, weights2, biases2)
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1))
cross_entropy_mean = tf.reduce_mean(cross_entropy)
regularizer = tf.contrib.layers.l2_regularizer(REGULARIZATION_RATE)
regularization = regularizer(weights1) + regularizer(weights2)
loss = cross_entropy_mean + regularization
learning_rate = tf.train.exponential_decay(LEARNING_RATE_BASE, global_step, mnist.train.num_examples / BATCH_SIZE,
LEARNING_RATE_DECAY)
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
# 每过一遍数据既需要通过反向传播来更新神经网络参数,又要更新每一个参数的滑动平均值,为了一次完成多个操作,
# TensorFlow提供了tf.control_dependencies和tf.group两种机制
with tf.control_dependencies([train_step, variables_averages_op]):
train_op = tf.no_op(name='train')
correct_prediction = tf.equal(tf.argmax(average_y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
with tf.Session() as sess:
tf.global_variables_initializer().run()
validate_feed = {x: mnist.validation.images, y_: mnist.validation.labels}
test_feed = {x: mnist.test.images, y_: mnist.test.labels}
for i in range(TRAINING_STEPS):
if i % 1000 == 0:
validate_acc = sess.run(accuracy, feed_dict=validate_feed)
print("After %d training step(s), validation accuracy using average model is %g" % (i, validate_acc))
xs, ys = mnist.train.next_batch(BATCH_SIZE)
sess.run(train_op, feed_dict={x: xs, y_: ys})
test_acc = sess.run(accuracy, feed_dict=test_feed)
print("After %d training step(s), test accuracy using average model is %g" %(TRAINING_STEPS, test_acc))
def main(argv = None):
# 该语句会自动将数据集下载到相应目录
mnist = input_data.read_data_sets("/home/fan/dataset/mnist/", one_hot=True)
train(mnist)
if __name__ == "__main__":
tf.app.run()
可见最后调用的时候,使用的是tf.app.run(),其意思为通过处理flag解析,然后执行main函数,如果你的函数入口不为main(),假设为test(),那么此处应该为tf.app.run(test()),当然,也等同于直接调用入口函数的效果(此处存疑,不过在上面的代码中是可以的)
在选择优化的时候,我们现在选择的是优化总损失,也可以选择优化交叉熵,但是,如果优化交叉熵的话,会使得模型过拟合从而在面临未知数据的时候表现的没有优化总损失好
变量管理
# 以下二者创建变量的方式等价
v = tf.get_variable("v", shape=[1], initializer=tf.constant_initializer(1.0))
v1 = tf.Variable(tf.constant(1.0, shape=[1]), name="v")
TensorFlow中的变量初始化函数
初始化函数 | 功能 | 主要参数
-- | --
tf.constant_initializer | 将变量初始化为给定常量 | 常量取值
tf.random_normal_initializer | 将变量初始化为满足正态分布的随机值 | 正态分布的均值和方差
tf.truncated_normal_initializer | 将变量初始化为满足正态分布的随机值,但如果随机出来的值偏离平均值超过2个标准差,那么这个数将被重新随机 | 正态分布的均值和标准差
tf.random_uniform_initializer | 将变量初始化为满足平均分布的随机值 | 最大、最小值
tf.uniform_unit_scaling_initializer | 将变量初始化为满足平均分布但不影响输出数量级的随机值 | factor(产生随机值时乘以的系数)
tf.zeros_initializer | 将变量设置为全0 | 变量纬度
tf.ones_initializer | 将变量设置为全1 | 变量纬度
如果要获取一个已经创建的变量,需要通过tf.variable_scope函数来生成一个上下文管理器,并明确指明在这个上下文管理器中,tf.variable将直接获取已经生成的变量
with tf.variable_scope("a"):
v = tf.get_variable("v", shape=[1], initializer=tf.constant_initializer(1.0))
with tf.variable_scope("a", reuse=True):
v1 = tf.get_variable("v", [1])
print(v == v1) # True
如上,当我们想要复用变量的时候,要设置reuse为True,否则则是另外创建
当上下文管理器嵌套的时候,如果内部的上下文管理器不设置reuse值,那么其将会保持和外层值一致
也可以在名称为空的命名空间中直接通过代命名空间名称的变量名来获取其他命名空间下的变量
with tf.variable_scope("", reuse=True):
v1 = tf.get_variable("a/v", [1])
print(v == v1) # True
TensorFlow模型持久化
TensorFlow提供了tf.train.Saver类来保存和还原网络模型
import tensorflow as tf
import os
v1 = tf.Variable(tf.constant(1.0, shape=[1], name='v1'))
v2 = tf.Variable(tf.constant(2.0, shape=[1], name='v2'))
result = v1 + v2
init_op = tf.global_variables_initializer()
saver = tf.train.Saver()
with tf.Session() as sess:
sess.run(init_op)
if not os.path.exists("saveModel"):
os.mkdir("saveModel")
saver.save(sess, 'saveModel/saveTest.ckpt')
如上,saver.save函数将把TensorFlow模型保存到saveModel/saveTest.ckpt文件中,但同时会在saveModel文件下出现额外的三个文件:checkpoint文件保存了一个目录下所有的模型文件列表,.meta文件保存了TensorFlow计算图的结构,.ckpt文件保存了TensorFlow程序中每个变量的取值
加载模型的方法:
v1 = tf.Variable(tf.constant(1.0, shape=[1], name='v1'))
v2 = tf.Variable(tf.constant(2.0, shape=[1], name='v2'))
result = v1 + v2
saver = tf.train.Saver()
with tf.Session() as sess:
saver.restore(sess, "saveModel/saveTest.ckpt")
print(sess.run(result))
以上,通过加载模型而不用初始化变量,从而使得变量变为模型中存储的值
也可以直接加载已经持久化的图:
import tensorflow as tf
saver = tf.train.import_meta_graph("saveModel/saveTest.ckpt.meta")
with tf.Session() as sess:
saver.restore(sess, "saveModel/saveTest.ckpt")
print(sess.run(tf.get_default_graph().get_tensor_by_name("add:0")))
以上程序默认保存和加载了TensorFlow计算图上定义的全部变量
可以提供一个列表给tf.train.Saver来指定需要保存或者加载的变量,如:saver = tf.train.Saver([v1]),如此将只会加载v1变量
可以在保存或加载时给变量重命名
v1 = tf.Variable(tf.constant(1.0, [1]), name="o-v1")
v2 = tf.Variable(tf.constant(2.0, [1]), name="o-v2")
saver = tf.train.Saver({"v1": v1, "v2": v2})



