AD阶段分类论文阅读笔记
A Deep Learning Pipeline for Classifying Different Stages of Alzheimer’s Disease from fMRI Data
-- Yosra Kazemi
阿尔茨海默氏病(AD)是一种不可逆转的渐进性神经障碍,会导致记忆和思维能力的丧失
该论文使用深度学习的方法成功地对AD病的五个阶段进行了分类:非病态健康控制(NC)、显著性记忆关注(SMC)、早期轻度认知损害 (EMCI)、晚期轻度认知损害(LMCI)和阿尔茨海默病(AD)
在进行分类之前,fMRI的数据经过严格的预处理以避免任何噪音;然后,利用AlexNet模型提取从低到高水平的特征并学习
阿尔茨海默病以不同的速率发展,每个个体可能在不同的时间经历不同的症状,在不同阶段的阿尔茨海默氏症中,类别间的差异很低。
阿尔茨海默病是痴呆的主要病因,不同类型的痴呆症包括:老年痴呆(AD)、路易体痴呆、额颞叶紊乱症和血管性痴呆
在阿尔茨海默病中,大脑细胞中某些蛋白质水平的变化会影响神经元在海马体区域的交流能力,因此阿尔茨海默氏症的早期症状是失忆
病人的大脑中有一些不正常的团块和缠结在一起的纤维束,它们分别被称为淀粉样斑块和神经纤维缠结。这些现在被认为是老年痴呆症的一些主要症状
研究人员认为AD病人在出现症状之前的20年或更多年以前,大脑就发生了变化
目前,对于AD的阶段没有很好的定义,一些专家为更好地理解疾病的进展使用了七阶段的模型
- 没有损伤
- 非常轻微的下降
- 轻微下降
- 温和的下降
- 中度严重下降
- 严重下降
- 非常严重下降
阿尔茨海默病协会将七个阶段概括为三个主要阶段:轻度、中度和重读
大多数机器学习特征提取方法的目标是最大化类间方差或最小化类内方差
在这项研究中,使用静息状态fMRI成像来区分阿尔茨海默病不同阶段之间的差异,关注的是大脑在疾病的不同阶段是如何变化的,而不是在活动中是如何变化的
该研究详细介绍:
数据集
使用ADNI数据库中的一个子集来训练和验证CNN分类器
需注意ADNI数据差异:
ADNI的扫描是在两种不同的特斯拉扫描仪上进行的,分别为飞利浦医疗系统和西门子:
飞利浦医疗系统:静息状态fMRI扫描序列(EPI)144卷,场强度=3.0特斯拉,翻转角度=80.0度,TE=30.0 ms,TR=3000.0 ms, 64 × 65矩阵,3.31 mm厚度的6720.0片,延长静息状态fMRI的EPI序列为200卷,场强度=3.0特斯拉,翻转角度=90.0度,TE=30.0 ms, TR=3000.0, 64 × 65矩阵,3.31 mm厚9600.0片
西门子:EPI序列为197卷,场强度=3.0 tesla,翻转角度=80.0度,TE=30.0 ms, TR=2999.99, 448 × 448矩阵,197片3.4 mm厚度
数据集类别信息:

数据预处理
预处理提高了分析的灵敏度,验证了统计模型的有效性
首先将DICOM格式的数据转换为NII格式的数据,使用dcm2nii toolbox
然后从fMRI数据中移除非大脑区域,使用FSL-BET toolbox
抖动修正,使用FSL-MCFLIRT toolbox
切片时序校正,使用Hanning- windowed Sinc插值 -- 证明体素时间序列对所有体素具有参考时序
空间平滑,使用Gaussian kernel of 5mm FWHM -- 保护底层信号的同时降低噪声水平
高通滤波,使用时域高通滤波器,截止频率为0.01 HZ -- 去除低电平无用信号,如呼吸、心跳
空间标准化,FSL‘s调情、注册MNI152标准空间 -- 为了分析数据需要相同的图片标准
MNI152标准空间: 152幅结构图像经过高维非线性注册后的均值
图像变换
为建立合适的数据集,最终将图片转换为PNG格式
方法
基于作者的实验测试,AlexNet与GoogleNet有近似的精确度,但是AlexNet需要的时间要少,因而选择了ALexNet作为CNN分类器
过拟合的原因是:参数和权重数量很大,但是样本量不足
防止过拟合的方法有:
- 增大数据集,降低模型复杂性
- 使用数据增强
- 使用正规化
AlexNet架构
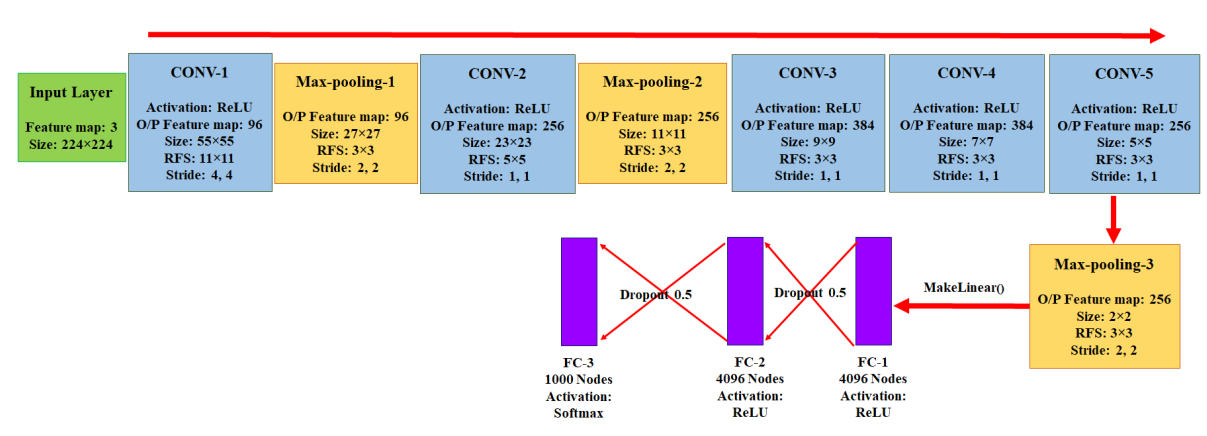
该研究使用的数据集的划分为:training : validation : testing = 0.6 : 0.2 : 0.2
该研究使用Caffe Deep Learning framework来训练模型,同时将数据集转换为Lightning Memory Mapped Database,将图片转换为256 × 256 像素
为在Caffe framework中实现模型,该研究调整AlexNEt模型为30 epochs,使用Caffe Stochastic Gradient Descent(SGD) solver方法
SGD solver方法使用的更新权重W的等式:
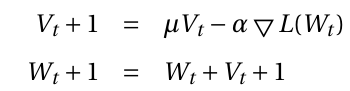
 是一个负梯度,vt是之前的权重更新参数,a是学习率,u是动量超参数
是一个负梯度,vt是之前的权重更新参数,a是学习率,u是动量超参数
初始化参数:

超参数:
学习率变化曲线:

经过多次迭代之后的动量将权重更新的大小乘1 / (1 - u)
最终使用的AlexNet架构:




