回溯算法
解决⼀个回溯问题,实际上就是⼀个决策树的遍历过程。你只需要思考 3 个问题:
- 路径:也就是已经做出的选择
- 选择列表:也就是你当前可以做的选择
- 结束条件:也就是到达决策树底层,⽆法再做选择的条件
回溯算法的框架:
result = []
def backtrack(路径, 选择列表):
if 满⾜结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
【举例 1】
全排列问题:
给定一个没有重复数字的序列,返回其所有可能的全排列。
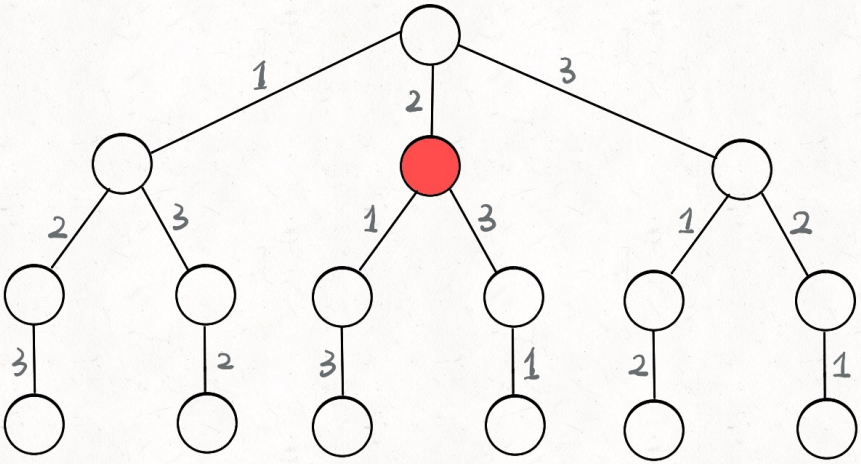
⽐⽅说给三个数[1,2,3],如下图,⽐如说你站在下图的红⾊节点上,则 [2] 就是「路径」,记录你已经做过的选择; [1,3] 就是「选择列表」,表⽰你当前可以做出的选择;「结束条件」就是遍历到树的底层,在这⾥就是选择列表为空的时候。
如此,回溯算法的核心框架可以表示为:
for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加⼊选择列表
我们只要在递归之前做出选择,在递归之后撤销刚才的选择(如树的遍历),就能正确得到每个节点的选择列表和路径,则全排列的详细代码为:
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> res;
vector<int> trace;
traceback(nums, trace, res);
return res;
}
void traceback(vector<int> &nums, vector<int> trace, vector<vector<int>>& res){
if(trace.size() == nums.size()){
res.push_back(trace);
return;
}
for(int item: nums){
if(find(trace.begin(), trace.end(), item) == trace.end()){
trace.push_back(item);
traceback(nums, trace, res);
trace.erase(trace.end()-1);
}
}
}
};
【举例 2】
N皇后问题:
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数 n ,返回所有不同的 n 皇后问题的解决方案。每一种解法包含一个不同的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
注:皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
class Solution {
public:
vector<vector<string>> solveNQueens(int n) {
vector<vector<string>> vvs;
vector<string> vs(n, string(n, '.'));
traceback(0, vs, vvs);
return vvs;
}
void traceback(int row, vector<string>& vs, vector<vector<string>>& vvs){
if(row == vs.size()){
vvs.push_back(vs);
return;
}
for(int i = 0;i < vs.size();i++){
if(!isValid(row, i, vs)) continue;
vs[row][i] = 'Q';
traceback(row+1, vs, vvs);
vs[row][i] = '.';
}
}
bool isValid(int row, int n, vector<string>& vs){
// 同一列
for(int i = 0;i < row;i++)
if(vs[i][n] == 'Q') return false;
// 左上斜线
for(int i = row-1, j = n-1; i >= 0 && j >= 0;i--,j--)
if(vs[i][j] == 'Q') return false;
// 右上斜线
for(int i = row-1, j = n+1; i >= 0 && j < vs.size();i--,j++)
if(vs[i][j] == 'Q') return false;
return true;
}
};




