计算机中使用的数理逻辑学习笔记
布尔代数运算律
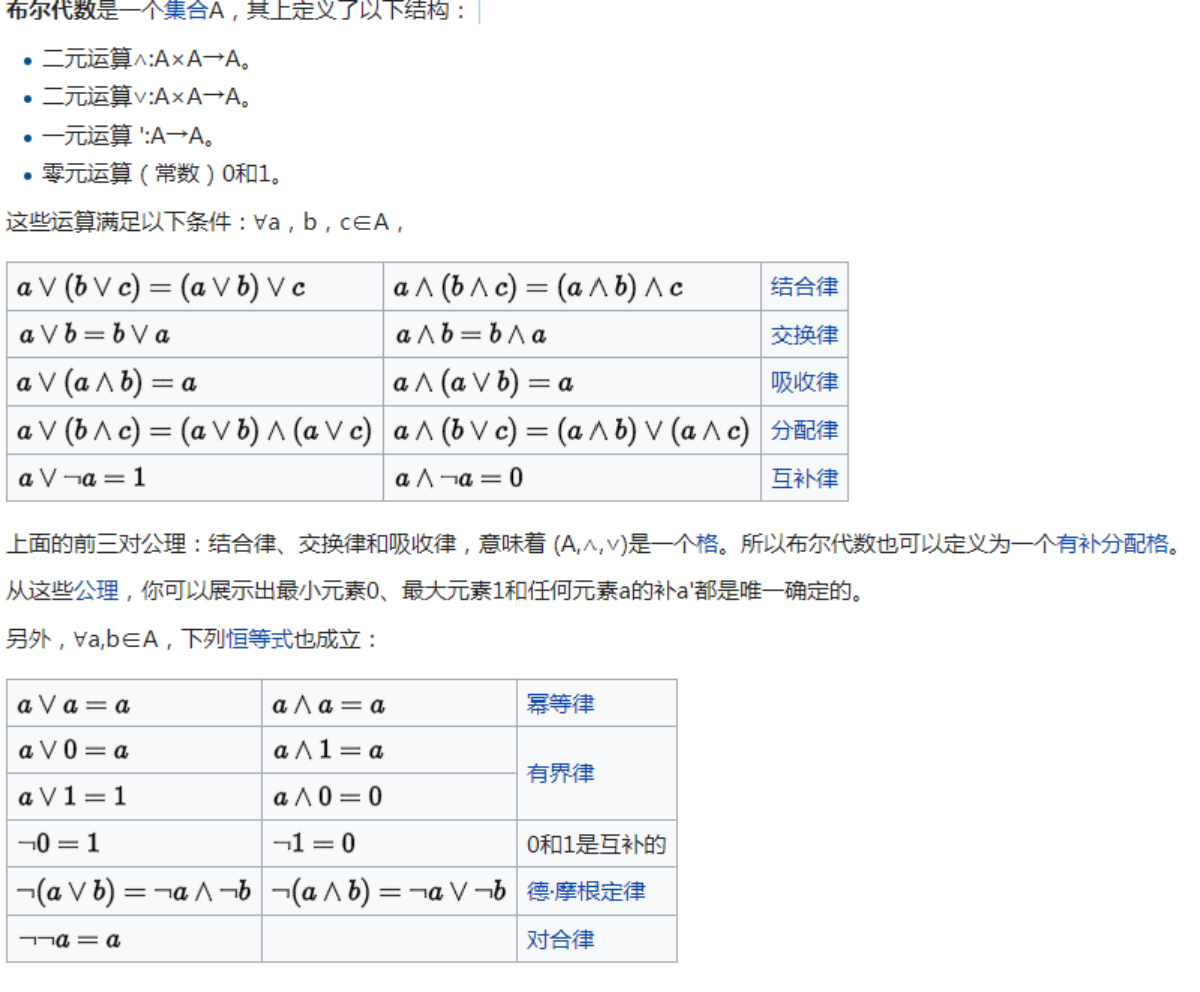
布尔运算等式变换
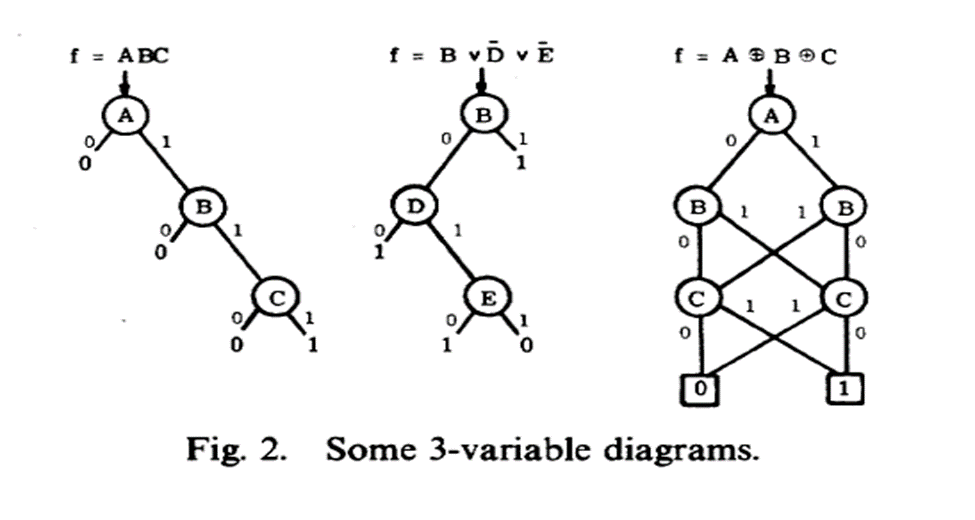
BDD(二元决策树)
BDD描述了一个过程,这个过程按照给定的值(0/1)进行向下搜索,直到终点。
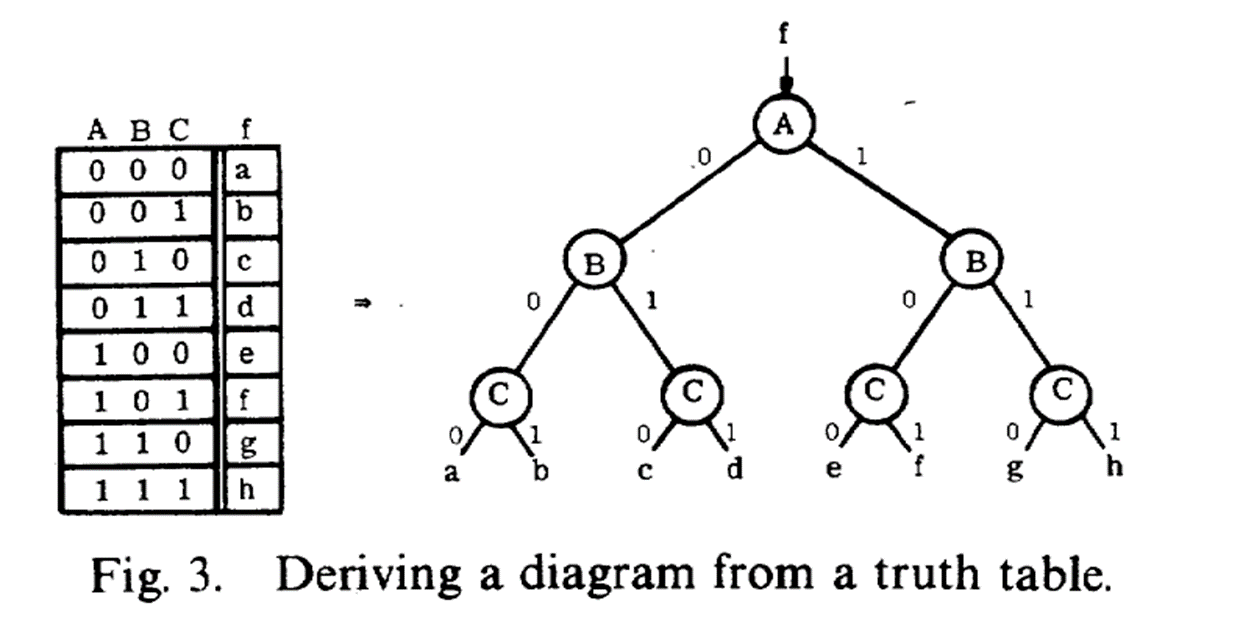
从真值表中派生(Derive)二元决策树:
化简:将冗余的部分去掉
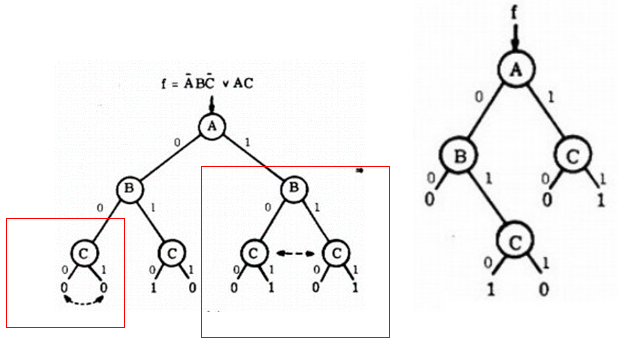
对于左边红框内,因为无论\(C\)取何值,最终的结果总是为0,因此\(C\)的存在对于该分支的结果并没有影响,因此可以将其删除。对于右边红框由\(B\)延伸到\(C\)处时,无论\(B\)取何值,总是延伸到相同的\(C\),因此在这里\(B\)的取值也对该分支没有影响,因此可以直接将\(B\)节点删除,从而得到了右图。
Shannon expansion formula(香农展开)
算法步骤:
- 固定一个变量,画出此变量的节点以及01分支
- 看是否有分支可以合并,如果可以则合并,否则再选取另一个变量转到步骤1
- 直到分支节点处变为0或1,则结束。
即:每次提取一个变量,将原来的表达式扩展为该变量取不同值的形式。
示例:

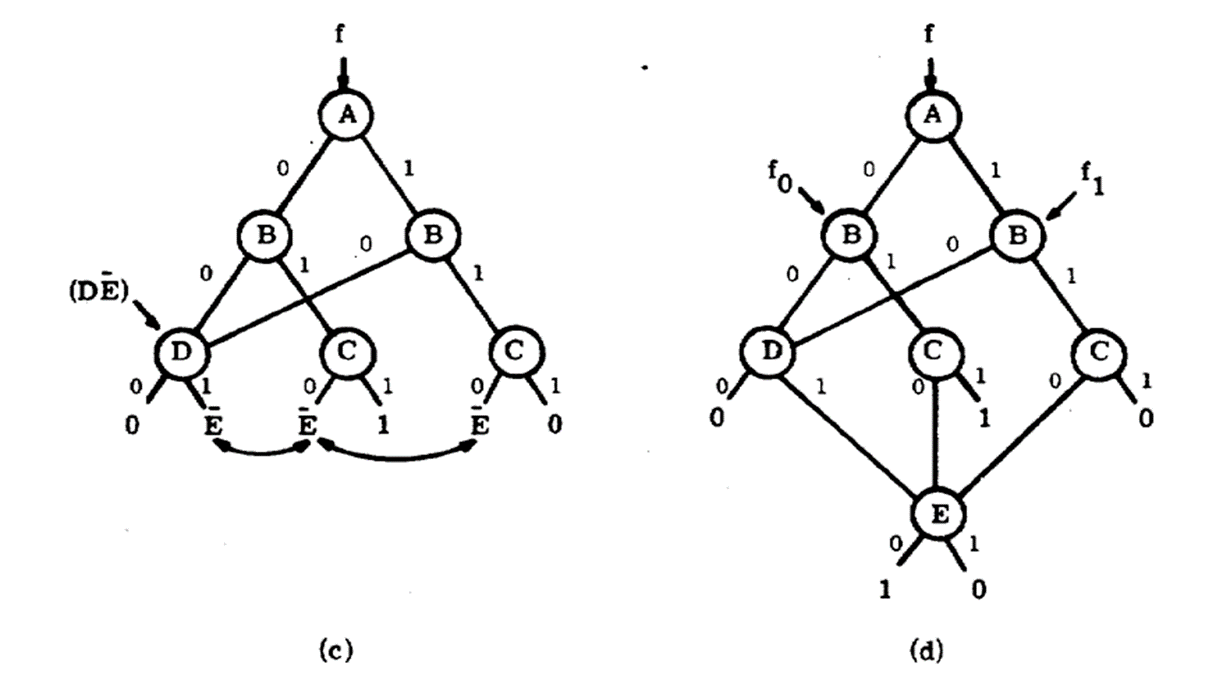
如图a所示,将\(A\)取值为0时,原表达式\(f\)进化为为\(f_0\),将\(A\)取值为1时,\(f\)进化为\(f_1\)。
BDD在计算机中的存储时,每个节点对应一个三元组:(变量名称,指针1,指针2)
其中,变量名称指定变量,指针1,指针2分别指定,当前变量取值分别为0或1时,应该指向的节点。
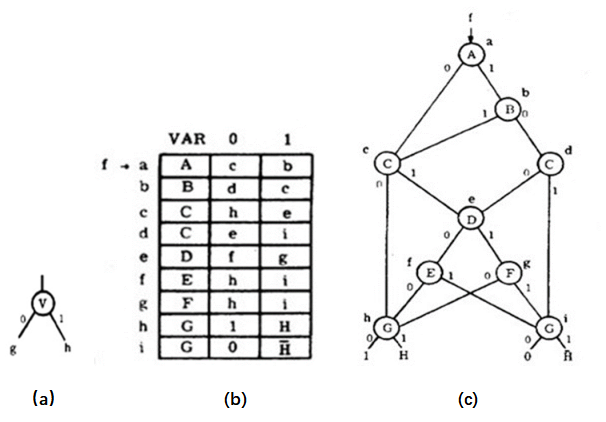
如(a)表示一个节点分支,则其在计算机中的存储可以表示为(V, g, h)。(b)表示了一组存储的三元组。(c)表示了(b)代表的BDD。
计算BDD的输出时,只需要沿着标识路径一直往下走即可,所到达的终止节点的值即为输出结果。
注:
- 一个节点的输出路径有且仅有一条是active path
- 从一个节点到0或1终点,有且仅有一条由active path组成的路径
计算“和的积”与“积的和”的个数
“和的积”的个数:主合取范式中,合取式的个数,即:使输出结果为0的路径数目。
“积的和”的个数:主析取范式中,析取式的个数,即:使输出结果为1的路径数目。
用分支的权值计算:
步骤:
- 最上层结点的两个分支权均赋值为1。
- 其余的结点的两个分支权均赋值为它所有入度权值的和。
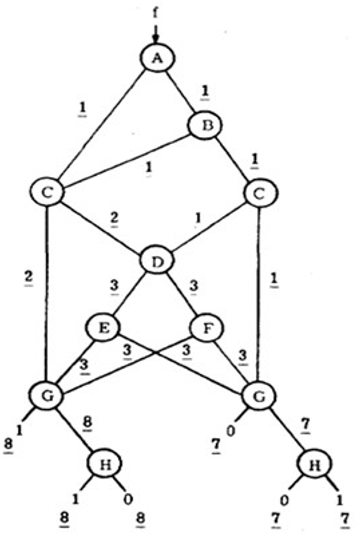
其中, 和的积(0): 8+7+7=22 积的和(1): (8+8+7=23)
图的简化(reduce) (ODBB)
简化后的函数图包含以下性质:
- 不包含左右子节点相同的节点
- 不包含这样的节点:分别以左右子节点为根节点的子图同形
注:在简化的图中,以每一节点为根的子图也是简化的。任意的布尔函数有唯一的简化图可以将其表示,使得图的节点数目最少
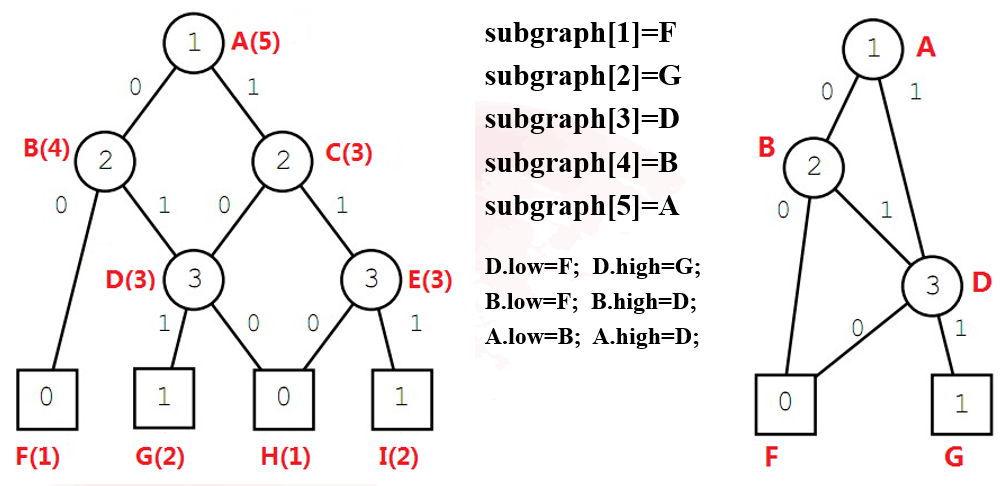
化简思想为:将原图按层排列,从终止节点(底层)依次向上进行标记,最后相同标记的只取一个节点就完成了图的简化。
样例:
第一步:将节点放到各层列表中,此处需要注意的是,要把终止节点全部都放在最后一层
第二步:从终止节点到根节点对每个list进行操作
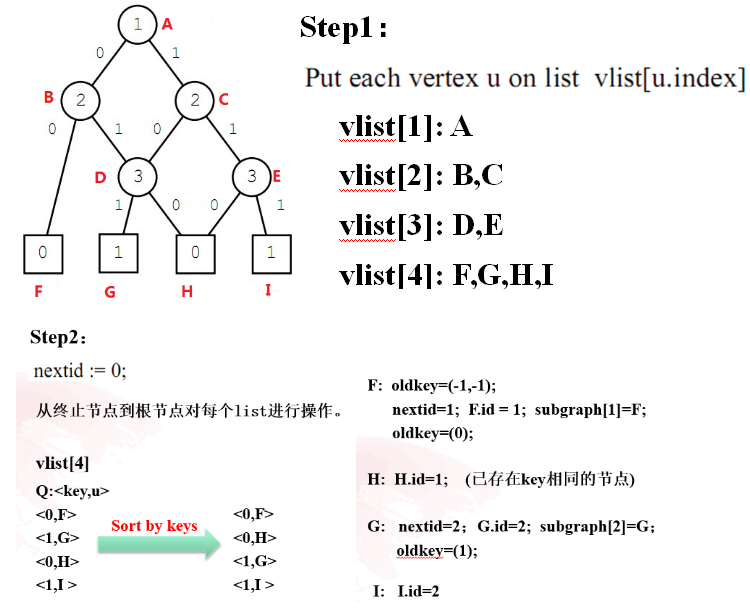
对于每个节点,oldkey的初始化均为(-1,-1),终止节点的oldkey最后应该只有一个0或1值,同时终止节点最终也应该至多只有两个id(1,2)和oldkey(0,1)
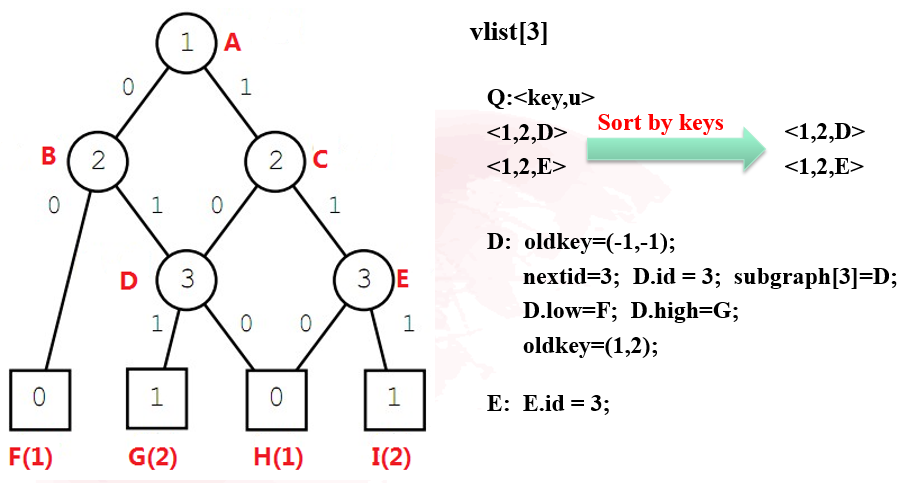
对于非终止节点,其oldkey最后为两个值,前一个值表示其取0时应该指向的节点id,另一个值表示其取1时应该指向的节点id。low,high分别表示其取0和1时指向的节点。
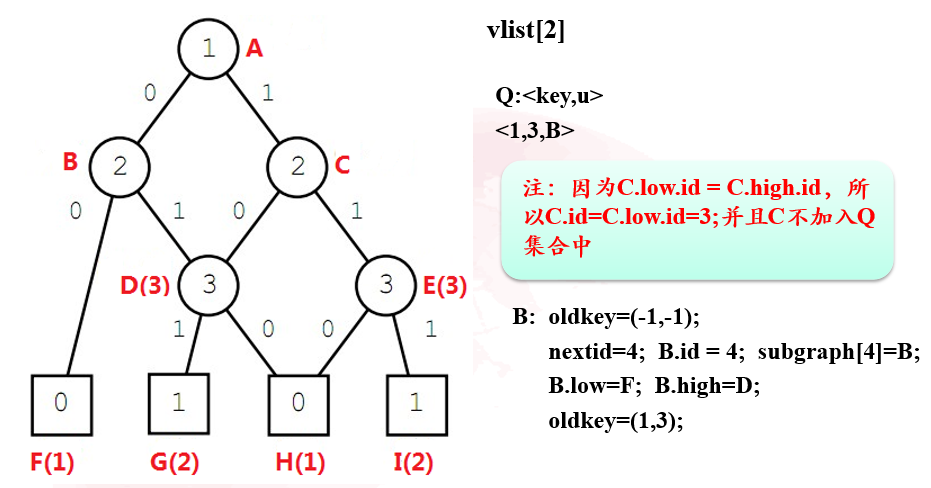
当某个节点的low值和high值相等时,说明该节点的取值对于该分支的最终结果并没有影响,因此可以直接删除该节点。

OBDD的Apply操作是通过深度优先搜索的方法,对一些已知的布尔函数 OBDD 表示进行二元布尔运算得到另外一些布尔函数 OBDD 表示的操作。整个过程从上至下进行,我们需要做的预备工作是给每个节点编号(1,2,3.... 每个都不相同),然后从顶层开始,用两个 OBDD 树的顶层的节点合成一个新的节点,合成的规则就三种:
- 两个节点都为叶节点,可以直接根据布尔运算得出结果,合成的节点也是叶节点。
- 如果有一个节点为非叶子节点,看这两个节点的 index 值是否一样,如果是一样的,比如两个节点都表示 x1,那么新节 点的 index 就是 x1,新节点的左孩子通过两个老节点的左孩子生成,新节点的右节点通过两个老节点的右孩子生成。
- 如果两个节点的 index 值不同,比如 index(u)\(<\)index(v),新节点的 index 为较小的 index(u),新节点的左孩子由 u 的左孩子与 v 生成,新节点的右孩子由 u 的右孩子与 v 生成,当 index(u)\(>\)index(v)反过来做即可。
举例:\(f=(x_1+x_2)*x_3+x_4,g=x_1*x_3^{'}+x_4\),求\(f+g\)的OBDD
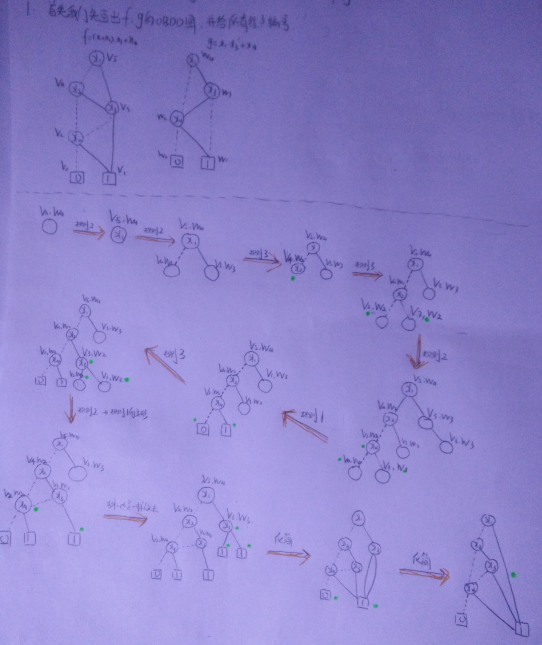
关于 OBDD 的 ITE 的实现过程
ITE操作是一个三元布尔操作符,对于具有相同变量序的三个布尔函数f、g和h,ITE操作可用来实现:if f then g else h。对于相同变量序:\(x_1<x_2<...<x_n\)下的布尔函数\(f,g\)和\(h\),\(ITE(f,g,h)=f\cdot g+f^{'}\cdot h\)
在算法中,常用小写 ite 来表示 ITE。下表给出了一些二元布尔运算的 ITE 操作实现:
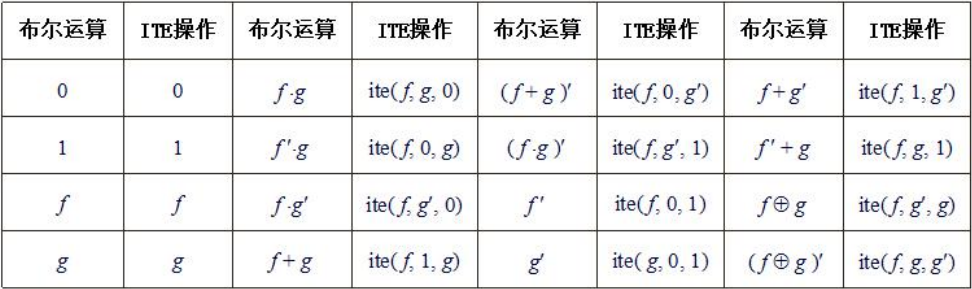
程序转化为逻辑表达式
FDS(Fair Discrete System)
一个Fair Discrete System(FDS) \(D = \lt V, O, \Theta, p, J, C \gt\)包括:
- \(V\):一组有限的类型化状态变量,一个V-state s表示V的一个解释
\( \sum_V \):表示所有的V-states集合 - \(O \subseteq V\): 可观察变量的集合
- $\Theta $:一个初始条件。一个描述初始状态的能够满足的断言
- \(p\):一个过渡关系。一个断言\(p(V, V^{'})\),引用状态变量的当前版本和即将变换成的版本。例如,\(x^{'}=x+1\)对应于赋值\(x:=x+1\)
- \(J={J_1,...,J_k}\):一个公平的(justice)需求集合。确保对于每个\(j_i,i=1,...,k\)的计算包含无限多个\(j_i\)-states。
- \(C=\lbrace <p_1,q_1>,...,<p_n,q_n>\rbrace\):一个包含compassion需求的集合。无限多个\(p_i\)-states意味着无限多个\(q_i\)-states。
例子:

- 首先表示\(V\),状态变量
a) 首先第一行就是程序最上面的初始化,左边两个变量一写,右边写个 natural。
b) 接下来定义$\pi \(,程序有几个部分(用||连接)就定义几个\)\pi \(,每个\)\pi \(对应的元素就是每一行语句\)𝑙_0$ ~ \(𝑙_𝑘\)
- 表示\(\Theta\)
\(\Theta\)表示初始条件,而初始时,每个\(\pi\)都处于第一行语句\(l_0\),再加上变量的初始化,把它们合取即可。
- 表示𝜌:表示𝜌之前得先说明几个定义:
- \(\pi^{'}\)可能在此表示下一个状态
- \(pres(V)\)。对于\(V\)里面的每个元素都可以这样表示:\(e=e^{'}\),然后把它们用合取符号连接起来。上面例子的\(press(V)\)就应该表示为:
- \(at\_l_j\)是一个缩写,表示\(\pi_i = l_j\),\(at^{'}\_l_j\)表示\(\pi_i^{'}=l_j\)
- \(p_I=press(V)\),\(p_{l_0}\)表示语句\(l_0\)转换成逻辑公式之后的一个符号。需要掌握\(p_{l_k}\)
- $p:p_I \vee p_{l_0} \vee p_{l_1} \vee p_{m_0} $
语句的表示
a) 赋值语句样例:\(y := e\)
进行该语句时,需要进行以下状态检查以确定该赋值语句是否能够成立。\(at\_l_j \wedge at^{'}\_l_k \wedge y^{'} = e\wedge pres(V-\lbrace \pi_i,y\rbrace)\)。
进行以上例题中的\(m_0\)赋值语句时,就应该表示成:\(p_{m_0}:\pi_2=m_0 \wedge \pi_2^{'}=m_1 \wedge \pi_1^{'} = \pi_1 \wedge x^{'} = 1 \wedge y^{'} = y\)
b) if语句:if b then \(l_1: S_1\) else \(l_2:S_2\)
如果这里没有else语句,那么\(l_2\)就是跳出if下一步要执行的语句
c) while语句:while b do [\(l_1:S_1\)]
上面例子\(l_0\)就可以表示为
- 表示\(J\):一般把\(!at\_l_j\)这个符号加入\(J\)集合中
上面例子的\(J\)集合可表示为
- 表示\(C\)。一般该集合为\(\empty\)
子句冲突规则
SAT
SAT: 给定一个命题公式,确定是否存在变量赋值以使该公式计算为真,这称为布尔可满足性问题。结果是,找到一个满足条件的解决方案或者证明不存在解决方案。
SAT问题的基本形式指给定一个命题变量集合\(X\)和一个\(X\)上的合取范式\(\varphi (X)\),判断是否存在一个真值赋值\(t(X)\),使得\(\varphi (X)\)为真。如果能找到,则称\(\varphi (x)\)是可满足的(satisfiable),否则称\(\varphi (x)\)是不可满足的(unsatisfiable)。SAT问题的模型发现形式指当\(\varphi (x)\)可满足时,给出使公式\(\varphi (x)\)可满足的一组赋值。
实际生产中的 NP 难题可以转化为 SAT 问题进行求解,因此,首先要进行规约和编码,目前 SAT 问题编码多采用 CNF 形式。DIMACS 作为标准格式广泛用于 CNF 布尔公式,也被历届 SAT 国际竞赛采用。 DIMACS 文件用字符 c 引导的注释文字行开始。紧接注释之后的一行 p cnf 表示该实例是 CNF 形式的公式,nbvar 指公式包含的变量数目,nbclauses 指公式包含的子句数目,要求1至 nbvar 之间的每个变量至少在某个子句中出现一次。然后下面各行是子句序列,每个子句由一系列互不相同的介于 -nbvar 和 nbvar 的非空数字组成,并以 0 结束。正的数字表示相应序号变量的正文字形式,负的数字表示对应序号变量的负文字形式。
最近几年的SAT国际竞赛结果证明,预处理技术对SAT求解器性能至关重要。早期的预处理技术使用原始 DPLL (DavisPutnamLogemannLoveland,简称DPLL)提出的单元传播和纯文字规则,后来发展了一些更复杂的技术如超二元解析、单元子句和探针等。
命题逻辑基于SAT Solver的DPLL可满足性判定算法
合取范式样例:\((p∨q∨r)∧(p∨┐q∨r)∧(┐p∨q∨r)\)
析取范式样例:\((p∧q∧r)∨(p∧q∧┐r)∨(p∧┐q∧r)∨(┐p∧q∧r)∨(┐p∧┐q∧r)\)
DPLL(Davis-Putnam-Logemann-Loveland)算法,是一种完备的、以回溯为基础的算法,用于解决在合取范式(CNF)中命题逻辑的布尔可满足性问题;也就是解决CNF-SAT问题。
DPLL 的核心思想就是依次对 CNF 实例的每个变量进行赋值,其搜索空间可以用一个二叉树来表示,树中的每个节点对应一个变量,取值只能为 0 或 1,左右子树分别表示变量取 0 或 1 的情况,从二叉树中根节点到叶子节点的一条路径就表示 CNF 实例中的一组变量赋值序列,DPLL 算法就是对这棵二叉树从根节点开始进行 DFS(深度优先搜索) 遍历所有的通路,以找到使问题可满足的解。
预处理:将公式转换为对应的合取范式(CNF)
DPLL 框架
- Iterative Description(迭代描述)
status = preprocess(); //预操作
if (status!=UNKNOWN) return status;
while(1) {
decide_next_branch(); //变量决策环节
while (true) {
status = deduce(); //推理环节(BCP)
if (status == CONFLICT) { blevel = analyze_conflict(); //冲突分析
if (blevel == 0) return UNSATISFIABLE; else backtrack(blevel);
//智能回溯,对应
}else if (status == SATISFIABLE) return SATISFIABLE;
else break;
}
}
- Recursive description(递归描述)
DPLL(formula, assignment){
necessary = deduction(formula, assignment);
new_asgnmnt = union(necessary, assignment);
if (is_satisfied(formula, new_asgnmnt))
return SATISFIABLE;
else if (is_conflicting(formula, new_asgnmnt))
return CONFLICT;
var = choose_free_variable(formula, new_asgnmnt);
asgn1 = union(new_asgnmnt, assign(var, 1));
if (DPLL(formula, asgn1)==SATISFIABLE)
return SATISFIABLE;
else {
asgn2 = union (new_asgnmnt, assign(var, 0));
return DPLL(formula, asgn2);
}
}
基于迭代的实现相对于基于递归的实现有以下优势:
- 递归速度慢且容易发生溢出,相对于迭代就有很多自身的劣势。
- 迭代具有非时间顺序回溯(智能回溯)的优势。
- 递归需要更多的内存存储空间。
以下讨论基于迭代框架。
算法框图:
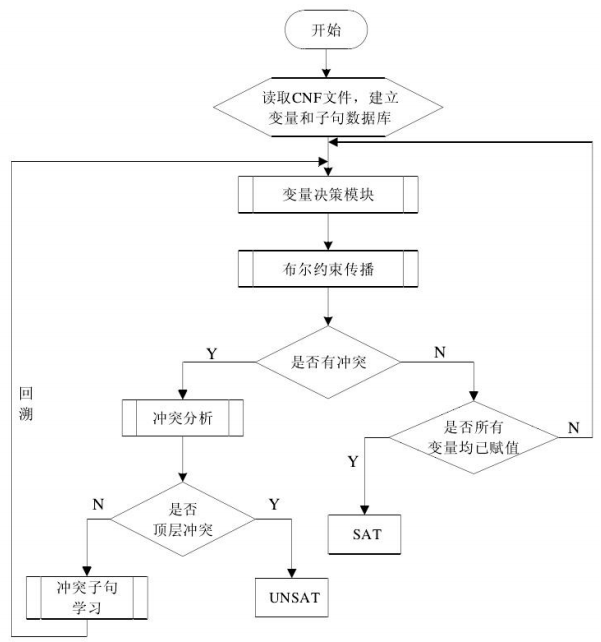
算法流程:
首先执行的是 preprocess()这个预处理操作,其实就是对 CNF 实例进行各种化简减轻后续的求解工作量。如果预处理不能直接 得出结果的话,就进行后面的 decide_next_branch()操作,这就是变量决策操作,它会分析从 哪个变量开始赋值是最合适的。对变量赋值以后,会执行一个deduce() 操作,可以管它叫推理操作,目的是识别该赋值所导致的必要赋值。 当然不正确的赋值可能会产生错误,这就会产生冲突,我们需要 analyze_conflict()分析这个冲 突得到冲突发生的根源位置,然后通过 backtrack()回溯到这个位置,为这个变量赋另外一个值, 继续往下搜索,如此循环,直到找到满足 SAT 的一组真值指派。如果回溯到了最顶层还没有解 决问题的话,那就表示这个 CNF 实例是不可满足的。
变量决策(decide_next_branch())
基于这样的一个事实:先对哪个变量进行赋值,会直接影响二叉搜索树的规模大 小,也就会影响求解时间,所以如何快速有效地决策出下一个将要赋值的变量,这很重要。以下将介绍四种变量决策方式:
- MOM(JW)方法
- Literal Count Heuristics 方法
- VSIDS 方法
- 一个改进的方法--(A Fast and Robust SAT Solver)
- MOM 法或者 JW 法
思想: 在一个子句中, 只要一个文字得到满足,那么这个子句就得到满足了。
所以,如果一个子句的长度越长(含有字母数越多),那么可以使得该子句满足的文字数目也就越多,这个子句也就越容易满足,所以它就不是所谓的“矛盾的主要方面”,我们不需要过于关注这个子句;然而,如果一个子句长度很小,那它就很不容易被满足,所以我们要优先考虑它们,给予它们更高的权重, 这样做的目的就是让那些不容易被满足的子句优先得到满足。
具体的方法是求解出和变量 \(l\) 相对应的 \(J\) 值,哪个变量 \(J\) 值大就选哪个先赋值,变量对应的 \(J\) 值的计算公式如下:
其中 \(l\) 表示变量,\(Ci\) 表示包含变量 \(l\) 的子句,共有 \(m\) 个子句, \(n_i\) 表示这个子句的长度。它体现出了 MOM 算法的两个关键点:“最短的子句”和“出现频率最高的变量”,”最短子句”体现在长度越短(\(n\) 越小), \(2^{-n_i}\) 的值就越大,它能给 \(J\) 值的贡献就越多;”出现频率最高的变量”体现在 \(l\) 出现次数越多的话,相加的项数就越多,\(J\) 值就更容易变的很大。
- Literal Count Heuristics 方法
它主要是统计已经给某些字母赋值但仍然没有得到满足 的子句的数量,这个数量依赖于变量赋值,所以每次换变量的时候,所有自由变量都需要重 新统计这个数量,效率较低。 - VSIDS,Variable State Independent Decaying Sum(独立变量状态 衰减和策略)
具体操作步骤如下:
- 为每一个变量设定一个 score,这个 score 的初始值就是该变量在所有子句集中出现的次数
- 每当一个包含该字母的冲突子句被添加进数据库,该字母的 score 就会加 1
- 哪个变量的 socre 值最大,就从这个变量开始赋值
* 另外,为了防止一些变量长时间得不到赋值,经过一定时间的决策后,每一个变量的 score 值都会被 decay,具体方式是把 score 值除以一个常数(通常为 2-4 左右)
推理(deduce())
当一个变量被赋值后,可以通过推理来减少一些不必要的搜索,加快效率。推理过程主要依赖于 Unit clause rule(单元子句规则),所谓单元子句就是:在这个子句中,除了一个文字未赋值 外,其他所有的文字都被赋值并体现为假,这样的子句就是 Unit clause(单元子句),剩下的 这个文字就是 unit literal(单元文字)。很容知道,在单元子句中,这最后一个文字必须体现 为真,整个子句才能被满足,把所有的单元文字都赋值并体现为真的过程就是 BCP(布尔约束 传播)。
BCP 的目标就是识别出单元子句并对单元文字赋值,能够减少搜索空间或提前逼出冲突。
以下将介绍三种BCP实现方法:
- counters 方法
- head/tail list 方法
- 2-literal watching 方法
counters 方法
具体做法是是为每个变量设置两个 lists,分别用来保存所有包含这个变量的正负字母的子句,并且每个子句都设置两个计数器,分别统计体现为真的字母数和体现为假的字母数。如果体现为假的字母等于总字母数,那就产生了冲突;如果体现为假的字母数比总字母数少 1,那就出现了单元子句,就需要对单元文字进行自动赋值。
举例
注:用\(!\)取代了逻辑非,因为不知道逻辑非怎么弄出来
初始的时候,1-8 号子句各有两个计数器(分别记录赋值为 0 和 1 的文字数量),一开始所有计数器的值都是 0。变量 \(m\) 有链表分别用来保存所有包含 \(m\) 和 \(!m\) 的子句,包含 \(m\) 的 链表中有子句 2,3,4,5,而包含 \(!m\) 的链表中有子句 1,7,8,其余变量也均有这样的两个链表。当给 \(m\) 赋 0 时,包含 \(m\) 的链表中的子句 2,3,4,5 的 0 计数器就会更新,数量加 1, 包含 \(!m\) 的链表中的子句 1,7,8 的 1 计数器也会更新,数量加 1;如果再给 \(p\) 赋 0 的话,包 含 \(p\) 的链表中的子句 1,2,3,8 的 0 计数器就也会更新,数量加 1,此时 2,3 两个子句的 0 计数器数量变为 2,比总文字数 3 少 1,均成为了单元子句,2 可以推出 \(q\) 必须赋 1,而 3 可以 推出 \(q\) 必须赋 0,产生冲突,BCP 完成任务。
head/tail list 方法
它为每个子句设置两个引用指针,分别是头指针和尾指针,初始时,头指针指向子句第一个文字,尾指针指向最后一个文字,每个子句的文字存放在一个数组中。对于一个变量 \(v\),设置有四个链表,分别装有句头是 \(v\) 的子句,句头是非 \(v\) 子句,句尾是 \(v\) 的子句, 句尾是非 \(v\) 的子句,分别标记为 clause_of_pos_head(v),clause_of_pos_tail(v), clause_of_neg_head(v),clause_of_neg_tail(v)。假设有 \(m\) 个子句的话,所有变量的四个链表中就共存放着 \(2m\) 个子句,无论后面这些子句怎么调换位置,子句总数是不变的。
因为是合取式,因此一共有2m个子句
假设某变量 \(v\) 被赋值为 1,那么所有句头和句尾为 \(v\) 的子句就都可以忽略了,因为他们已经被满足了。而对于句头或句尾是非 \(v\) 的子句,就需要移动头尾指针寻找下一个未被赋值的字母,头指针往后移,尾指针往前移,移动时可能会发生以下四种情况:
- 第一个遇到的文字 \(l\) 已经体现为真了,那么子句就已经满足了,什么都不用做,忽略这个子句就行了。
- 第一个遇到的文字 \(l\) 是未赋值的,且不是句尾,那么就把这个子句 \(c\) 从 \(v\) 的链表中移除,放入到 \(l\) 的对应的链表中。
- 如果头尾之间只剩一个变量未赋值,其他文字都体现为假了,就出现了单元子句,直接推断出单元文字的取值。
- 如果头尾之间所有文字都体现为假,那产生冲突,需要回溯。当一个变量被赋值的时候,平均有 m/n 个子句需要更新(m 为子句数,n 为变量数)。
举例
初始时,我们可以将各个子句填入变量的链表中,如下表所示:

此时,头尾指针分别指向每个子句的头部和尾部。当我们给 \(m\) 赋值为 0 的时候,\(m\) 的 clause_of_neg_head(m)链表中的子句 1,7,8 就可以忽略不看了,因为已经被满足,把它们标注为绿色,而 clause_of_pos_head(m) 中的子句 2,3,4,5 还没有被满足,这些子句头指针需要后移一位,转移后这些子句的头指针指向的文字就不是 \(m\) 了,所以需要将表格中 2,3,4,5 的位置换一下,更换位置的子句用红色标注,这次赋值后结果如下:
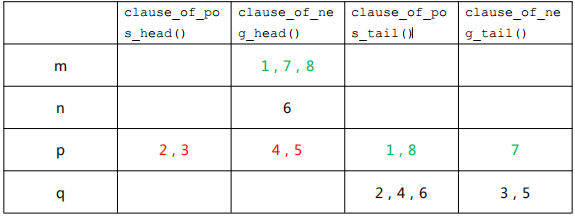
以此类推,当我们再给 \(p\) 赋 0 的时候,4,5 就可以不用考虑了,2,3 的头指针需再后移一位,2,3 在表格中的位置也需要更换,如下表所示:

此时已经满足条件(3)了,形成了两个单元子句,2 可以推出 \(q\) 必须赋 1,而 3 可以推 出 \(q\) 必须赋 0,产生冲突,BCP 完成任务。
2-literal watching
这个方法与 H/T 类似,也要为每个子句关联两个指针,与 H/T 不同之处是,这两个指针没有先后次序,也就没有所谓的头和尾的概念,这样设置会带来很多好 处,比如初始时这两个指针的位置可以是任意的(H/T 必须放在头和尾的位置),移动时也可 以向前后两个方向移动(H/T 中头指针只能向后移,尾指针只能向前移),回溯时无需改动指针的位置(W/T 回溯时需要把指针变回原来的位置)。但这种设置也有弊端,即只有遍历完所 有子句的文字后,才能识别出单元子句。相对应的,每个变量 v 也设置了两个 list 来分别存放以 watching 指针分为 v 以及非 v 的子句。接下来的操作都与 W/T 类似,当某个变量 v 赋值为 1 的话,watching 指针为 v 的子句可以忽略,watching 指针为非 v 的子句开始移动指针。
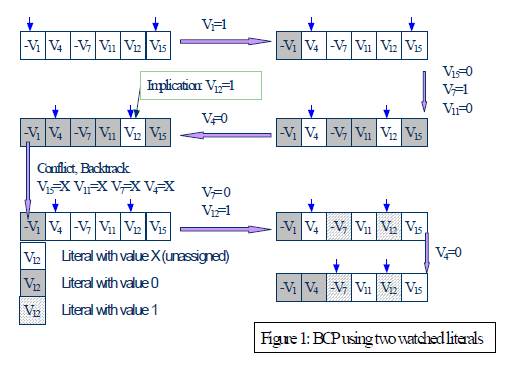
冲突分析与学习(analyze_conflict())
目的: 是找到冲突产生的原因,这就是分析的过程;并告诉 SAT 处 理器这些搜索空间是会产生冲突的,以后不要再踩这些坑了,这就是学习的过程。
早期解决冲突的方法就是回到上一层,将变量取值翻转,继续往下进行搜索,这也叫时序回 溯。但是这样做的结果很可能是冲突依旧存在,因为上一层的赋值也许并不是冲突产生的根本原 因,从而白白浪费一次计算的时间,效率非常低。目前主流的 SAT 处理器都采用基于冲突分析和学习的非时序回溯算法,它可以智能地分析 出冲突产生的根本原因,并回跳多个决策层,并把会导致冲突的子句加入到子句集中。
以下为一次冲突分析和学习的例子:
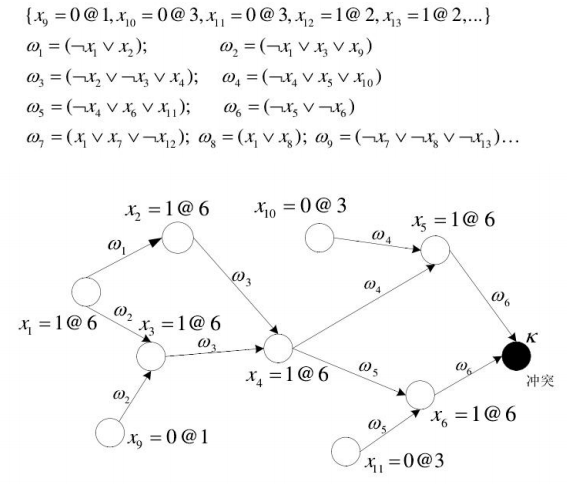
从图中我们可以看出,导致冲突产生的根本原因是第 1 层中将 \(x_9\) 赋为 0,在第 3 层中 将 \(x_{10}\) 赋为 0,在第 3 层中将 \(x_{11}\) 赋为 0,在第 6 层中将 \(x_1\) 赋为 1(\(x_1\)=1@6 表示在第 6 层将 x1 赋值为 1)。由此我们可以直接回溯到第 3 层进行重新赋值,而不是仅仅回溯到上一层,并且我们知道$(x_9 = 0) \cap (x_{10} = 0) \cap (x_{11} = 0) \cap (x_1 = 1) \(会导致冲突,我们就可以添 加子句\)w_{10} = (x_9 \cup x_{10} \cup x_{11} \cup !x_1)$ 添加进子句库中,在接下里的搜索过程中就能预防相同的变量赋值再次出现。
相关代码:
analyze_conflict(){
cl = find_conflicting_clause(); // 找到冲突子句 cl
while (!stop_criterion_met(cl)) {
lit = choose_literal(cl); // 选择一个文字
var = variable_of_literal( lit ); //这个文字所对应的变量命名为var
ante = antecedent( var ); // ante 为一个单元子句
cl = resolve(cl, ante, var);
// resolve()返回一个子句,除了 var 所对应的文字,这子句需要包含 cl 和 ante 中的
// 所有文字,其中 cl 是一个冲突子句,ante 是一个单元子句,所以返回的 cl 也是一个冲突子句
}
add_clause_to_database(cl);
back_dl = clause_asserting_level(cl);
return back_dl;
}
数据的存储方式
数据存储方式主要包括以下三种:
- 早期的链表和指针数组的存储方式
- 数组方式
- trie 存储方式
各个方法优缺点:
数组方式:数组采用连续空间存储,内存利用率和存储效率更高,局部访问能力更强。连续存储能提高,cache 命中率,从而增加计算速度。但不灵活。
链表方式:便于对子句进行增加和删除操作,存储效率低。因为缺少局部访问能力,往往会造成缓存丢失。
head/tail 和 2-literal watching 都被称为“膨胀数据结构”,它们都采用数组存储子句,最具竞争力。
以下主要介绍Tire数据存储方式。
Tire 是以三叉树的方式存储,它的每个内部节点都是都是一个变量的索引,从根节点到叶节点路径上的所有变量组成一个子句。每个节点的三条孩子边分别被标记为 Pos(positive)、Neg(negative)和 DC(dont care),例如节点 v 的 Pos 边表示文字 v,Neg 边表示文字 !v ,DC 边表示没有这个变量的文字。Tire 的叶节点是 T 或者 F,T 表示 CNF 实例中有这个子句,F 表示没有这个子句。下面是文中给出的一个例子:
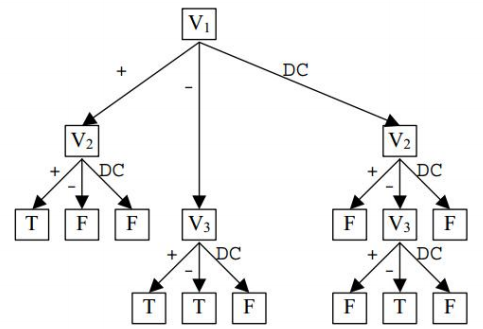
从图中我们可以清楚地看出这个 CNF 实例中有哪些子句,以 \(V_1\) 的左孩子的三条路径举例,第一条路径从根节点到叶节点为\((V_1,+),(V_2,+),T,\)表示\((V_1+V_2)\)这个子句是存在的;第二条路径从根节点到叶节点为\((V_1,+),(V_2,-),F,\)表示\((V_1+ !v_2)\) 这个子句是不存在的;第三条路径从根节点到叶节点为\((V_1,+),(V_2,DC),T,\)表 示\((V1)\)这个子句是不存在的,以此类推,可以得出所有的子句,$ (V_1+V_2)(V_1^{'}+V_3) (V_1^{'} +V_3{'})(V_2+V_3^{'})$。
Alloy
Alloy搜索的方法是:我给定一个定义域范围,对这个范围里所有的定义值都进行检查。本质是找语句中为假的可能,证明命题为假,因为为假说明命题一定错。
基础语法
sig: 类似于class
pred: 用来定义谓词
举例:
sig Platform {}
// there are "Platform" things
sig Man{ceiling, floor: platform}
// each Man has a ceiling and a floor Platform
pred Above(m, n: Man){
m.floor = n.ceiling
}
// Man m is "above" Man n if m's floor is n's ceiling
其中m,n:Man表示m,n都是Man的实例
fact: 用来定义已知条件
举例:
fact {
all m: Man | some n: Man | Above (n, m)
}
// one Man's ceiling is another Man's floor
该示例表示对于任意人来说,都存在某个人在他的上面
assert:表示假设
check: 用于检验
assert BelowToo{
all m: Man | some n: Man | Above(m, n)
}
// one Man's floor is another Man's ceiling ?
check BelowToo for 2
// check "one Man's floor is another MAn's ceiling"
// counterexample(反例) with 2 or less platform and men?
for 2:表示范围,用于举例的实例个数。这里表示有2个Man和两个platform。我们的目标是找出不满足BelowToo的反例来证明该命题是错误的。这里一共有2^4种可能,首先第一步,我们就要排除掉不满足fact的,因为fact是已知条件,如果不满足fact,则不考虑。然后再在剩下的结果中找出不满足假设的,若找到,则证明假设有错误。
找出的一个反例如下:
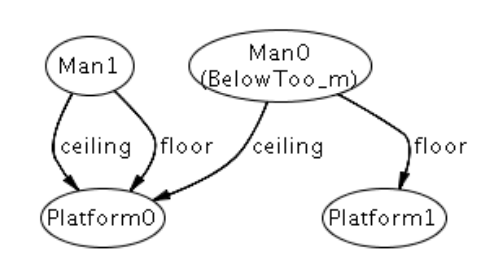
从此可以看出对于Man1,Man0在他的下面,但是对于Man0来说,没有人在他下面,所以这种情况就不满足假设。
注:当我们举例时要注意考虑所有情况,而不是自己假设存在的合理情况,比如这里,Man1就在自己的上面,但是它依旧符合fact
abstract:定义抽象,同java
all x: e | F // all: F holds for every x in e
all x: e1, y: e2 | F
all x, y: e | F
all disj x, y: e | F
some: F holds for at least one x in e
no: F holds for no x in e
one: F holds for exactly one x in e
lone: F holds for at most one x in e
set: any number
disj: short of distinct
举例:
some n: Name, a: Address | a in n.address
// some name maps to some address — address book not empty
no n: Name | n in n.^address
// no name can be reached by lookups from itself — address book acyclic
all n: Name | lone a: Address | a in n.address
// every name maps to at most one address — address book is functional
all n: Name | no disj a, a': Address | (a + a') in n.address
// no name maps to two or more distinct addresses — same as above
RecentlyUsed: set Name
// RecentlyUsed is a subset of the set Name
^: 表示传递闭包
+: 表示并集
-: 表示差集
in: 表示子集
.: 表示点乘,和数据库中的left join相同,但是结果中会去掉相同的那一项
#r: r中的元组数
&: intersection,交集
=: 表示判等
->: 交叉商,笛卡尔乘积
[]: 相当于按key取值
~: 转置
*: 自反传递闭包
{(N0)} + {(N1)} = {(N0), (N1)}
{(N0)} = {(N1)} = false
{(N0)} in none = false
{N0}.{N0, N1} = {N1}
{(N1), (N2)} & {(N0), (N2)} = {(N2)}
{(N0, A0), (N1, A1)} & {(N0, A0), (N1, A2)} = {(N0, A0)}
{(N0), (N1)} -> {(A0), (A1)} = {(N0, A0), (N0, A1), (N1, A0), (N1, A1)}
e1[e2] = e2.e1
a.b.c[d] = d.(a.b.c)
{(N0, A0), (N1, A0), (N2, A2)}[{(N1)}] = {(A0)}
~{(N0, N1), (N1, N2), (N2, N3)} = {(N1, N0), (N2, N1), (N3, N2)}
^{(N0, N1), (N1, N2), (N2, N3)} = {(N0, N1), (N0, N2), (N0, N3), (N1, N2), (N1, N3), (N2, N3)}
*{(N0, N1), (N1, N2), (N2, N3)} = {(N0, N0), (N0, N1), (N0, N2), (N0, N3), (N1, N1),
(N1, N2), (N1, N3), (N2, N2), (N2, N3), (N3, N3)}
<:: 域约束,第一个集合中元组后面的值在在后面指定的集合中
:>: 范围约束,后面集合中元组前面的一个值在后面指定的集合中
++: 相当于继承+重载
p ++ q = p – (domain(q) <: p) + q
{(N0, N1), (N1, N2), (N2, A0)} :> {(A0)} = {(N2, A0)}
{(N0, N1), (N1, N2), (N2, A0)} :> {(N0), (N1), (N2)} = {(N0, N1), (N1, N2)}
{(N0), (N1)} <: {(N0, N1), (N1, N2), (N2, A0)} = {(N0, N1), (N1, N2)}
{(N0, N1), (N1, N2), (N2, A0)} ++ {(N0, N1), (N1, A0)} = {(N0, N1), (N1, A0), (N2, A0)}
let: 定义局部变量
if f then e1 else e2: if语句
all n: Name |
some n.workAddress => n.address = n.workAddress
else n.address = n.homeAddress
all n: Name |
let w = n.workAddress, a = n.address |
some w => a = w else a = n.homeAddress
all n: Name |
let w = n.workAddress |
n.address = if some w then w else n.homeAddress
all n: Name |
n.address = let w = n.workAddress |
if some w then w else n.homeAddress
团
团与最大团:无向图G中任何两个节点均有边连接节点子集称为团。若C是无向图G的一个团,并且不能再加进任何一个G的结点使其成为一个更大的团,则称此C为最大团。也就是最大团就是不能被其他团所包含的一个团。

团:
{X2,X4},{X1,X2},{X3,X5},{x1,x3},{x2,x5},
最大团:
{X2,X4},{X1,X2},{X3,X5},{x1,x3},
条件随机场
判别模型: 根据所提供的features进行学习,最后在不同的数据分类之间画出了一个明显或者比较明显的边界。
生成模型: 先从训练样本数据中,学习所有的数据的分布情况,最终确定一个联合分布,来作为所有的输入数据的分布。对于新的样本数据(inference)对应的结果,通过学习到的模型的联合分布 ,再结合新样本的特征,通过条件概率就能计算出来 。
有向图的联合概率分布:
例如:
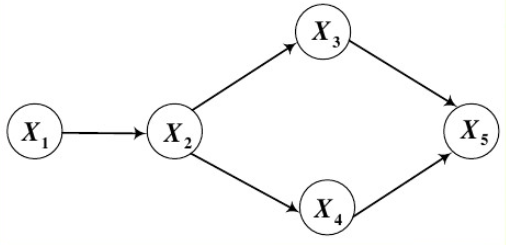
图中的概率如下:
基于计数器的BCP算法是一种容易理解与实现的 BCP 算法。假设每个子句(clause)拥有两个计数器(counter),一个用于子句中的值1字面量(literal)的计数,一个用于子句中的值0字面量的计数。每个变量(variable)都有两个列表,其中包含所有子句,其中该变量分别显示为正值和负值。当为变量分配一个值时,包含此字面量的所有子句将更新其计数器。设实例具有m个子句(clause)和n个变量(variable),并且平均每个子句具有l个字面值(literal)。那么每当给一个变量赋值时,有多少个计数器(counter)需要更新。简要概述分析过程。
答:l/n表示每个变量平均在每个子句中出现的次数,然后乘以子句的数量m,所以,有一个变量被赋值的时候,会有平均 ml/n 个计数器需要更新,在回溯的时候,每取消一个变量赋值,也会平均有 ml/n 个计数器的更新。
参考链接
© 12/28/2019 contributed by Fan zhonghao



