ResNet 论文研读笔记
Deep Residual Learning for Image Recognition
摘要
深度神经网络很难去训练,本文提出了一个残差学习框架来简化那些非常深的网络的训练,该框架使得层能根据其输入来学习残差函数而非原始函数。本文提出证据表明,这些残差网络的优化更简单,而且通过增加深度来获得更高的准确率
引言
深度网络很好的将一个端到端的多层模型中的低/中/高级特征以及分类器整合起来,特征的等级可以通过所堆叠层的数量来丰富。有结果显示,模型的深度发挥着至关重要的作用
在深度的重要性的驱使下,出现了一个新的问题:训练一个更好的网络是否和堆叠更多的层一样简单呢?解决这一问题的障碍便是困扰人们很久的梯度消失/梯度爆炸,这从一开始便阻碍了模型的收敛。归一初始化(normalized initialization)和中间归一化(intermediate normalization)在很大程度上解决了这一问题,它使得数十层的网络在反向传播的随机梯度下降(SGD)上能够收敛。当深层网络能够收敛时,一个退化问题又出现了:随着网络深度的增加,准确率达到饱和(不足为奇)然后迅速退化。意外的是,这种退化并不是由过拟合造成的,并且在一个合理的深度模型中增加更多的层却导致了更高的错误率
深层"plain"网络的在CIFAR-10上的错误率

退化的出现(训练准确率)表明了并非所有的系统都是很容易优化的。本文提出了一种深度残差学习框架来解决这个退化问题。方法是让这些层来拟合残差映射,而不是让每一个堆叠的层直接来拟合所需的底层映射。假设所需的底层映射为\(H(x)\),让堆叠的非线性层来拟合另一个映射:\(F(x):=H(x)−x\)。 因此原来的映射转化为:\(F(x)+x\),研究者推断残差映射比原始未参考的映射(unreferenced mapping)更容易优化,在极端的情况下,如果某个恒等映射是最优的,那么将残差变为0比用非线性层的堆叠来拟合恒等映射更简单
公式 F(x)+x 可以通过前馈神经网络的“shortcut连接”来实现,Shortcut连接就是跳过一个或者多个层。shortcut 连接只是简单的执行恒等映射,再将它们的输出和堆叠层的输出叠加在一起。恒等的shortcut连接并不增加额外的参数和计算复杂度。完整的网络仍然能通过端到端的SGD反向传播进行训练,并且能够简单的通过公共库(例如,Caffe)来实现而无需修改求解器
一个残差网络构建块(Fig.2)

本文表明
- 极深的残差网络是很容易优化的,但是对应的“plain”网络(仅是堆叠了层)在深度增加时却出现了更高的错误率
- 深度残差网络能够轻易的由增加层来提高准确率,并且结果也大大优于以前的网络
深度残差学习
残差学习
将\(H(x)\)看作一个由部分堆叠的层来拟合的底层映射,其中\(x\)是这些层的输入。假设多个非线性层能够逼近复杂的函数,这就等价于这些层能够逼近复杂的残差函数,例如,\(H(x) - x\)。我们明确地让这些层来估计一个残差函数:\(F(x):=H(x)−x\)而不是\(H(x)\)。因此原始函数变成了:\(F(x)+x\)。尽管这两个形式应该都能够逼近所需的函数,但是前者更易学习。使用这种表达方式的原因是之前提到的退化问题,使用残差学习的方式重新表达后,如果恒等映射是最优的,那么求解器将驱使多个非线性层的权重趋向于零来逼近恒等映射。如果最优函数更趋近于恒等映射而不是0映射,那么对于求解器来说寻找关于恒等映射的扰动比学习一个新的函数要容易的多,实验表明,学习到的残差函数通常只有很小的响应,说明了恒等映射提供了合理的预处理
通过捷径进行identity mapping
在堆叠层上采取残差学习算法,一个构件块如上图(Fig.2)所示,其定义为(Eq.1)
其中\(x\)和\(y\)分别表示层的输入和输出。函数\(F(x, {Wi})\)代表着学到的残差映射,该shortcut连接没有增加额外的参数和计算复杂度
在Eq.1中,\(x\)和\(F\)的维度必须相同,如果不同,可以通过shortcut连接执行一个线性映射\(W_s\) 来匹配两者的维度(Eq.2)
实验表明,恒等映射已足够解决退化问题,并且是经济的,因此\(W_s\)只是用来解决维度不匹配的问题
不仅是对于全连接层,对于卷积层残差连接也是同样适用的。函数\(F(x, {W_i})\)可以表示多个卷积层,在两个特征图的通道之间执行元素级的加法
网络架构
VGG、普通网络与残差网络的配置对比
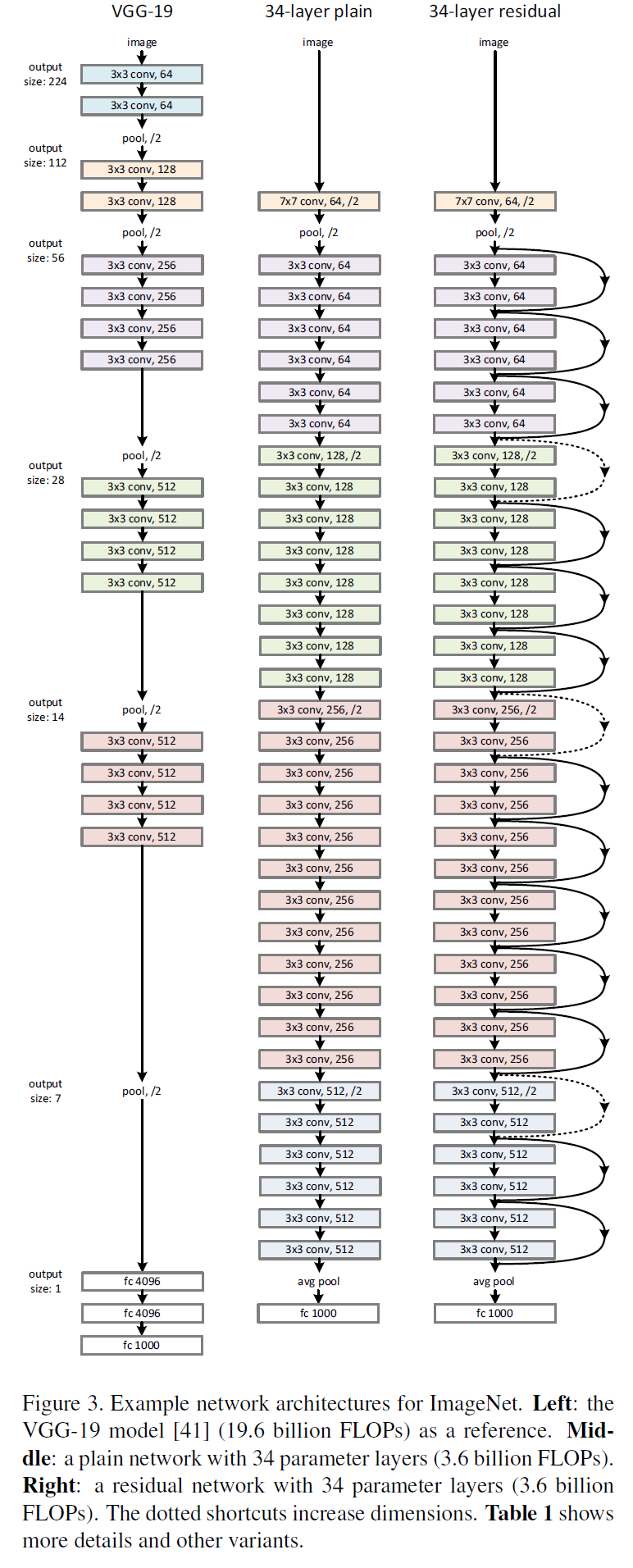
详细架构
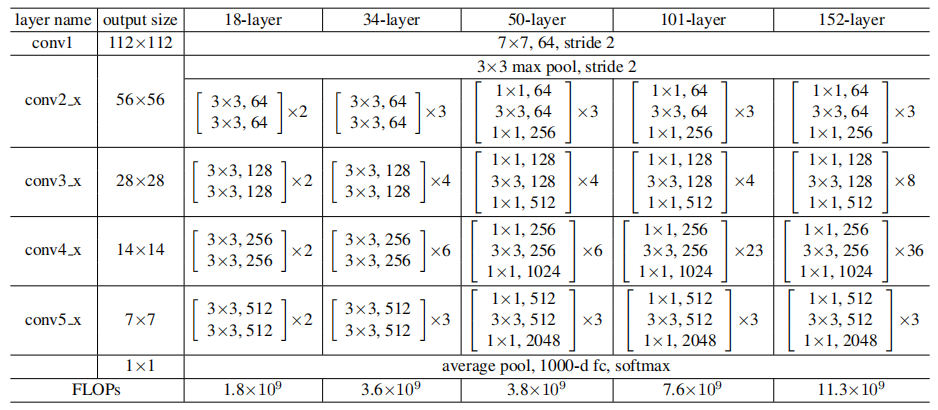
普通网络
卷积层主要为3*3的滤波器,并遵循以下两点要求
- 输出特征尺寸相同的层含有相同数量的滤波器
- 如果特征尺寸减半,则滤波器的数量增加一倍来保证每层的时间复杂度相同
直接通过stride为2的卷积层来进行下采样。在网络的最后是一个全局的平均pooling层和一个1000 类的包含softmax的全连接层。加权层的层数为34
残差网络
在普通网络的基础上,插入shortcut连接,将网络变成了对应的残差版本。如果输入和输出的维度相同时,可以直接使用恒等shortcuts(Eq.1)(残差连接实线部分),当维度增加时(残差连接虚线部分),考虑两个选项
- shortcut仍然使用恒等映射,在增加的维度上使用0来填充,这样做不会增加额外的参数
- 使用Eq.2的映射shortcut来使维度保持一致(通过1*1的卷积)
对于这两个选项,当shortcut跨越两种尺寸的特征图时,均使用stride为2的卷积
实验
普通网络
实验表明34层的网络比18层的网络具有更高的验证错误率,比较了训练过程中的训练及验证错误率之后,观测到了明显的退化现象----在整个训练过程中34 层的网络具有更高的训练错误率,即使18层网络的解空间为34层解空间的一个子空间
残差网络
实验观察到以下三点
- 34层的ResNet比18层ResNet的结果更优。更重要的是,34 层的ResNet在训练集和验证集上均展现出了更低的错误率。这表明了这种设置可以很好的解决退化问题,并且可以由增加的深度来提高准确率
- 与对应的普通网络相比,34层的ResNet在top-1 错误率上降低了3.5%,这得益于训练错误率的降低,也验证了在极深的网络中残差学习的有效性
- 18层的普通网络和残差网络的准确率很接近,但是ResNet 的收敛速度要快得多
错误率比较
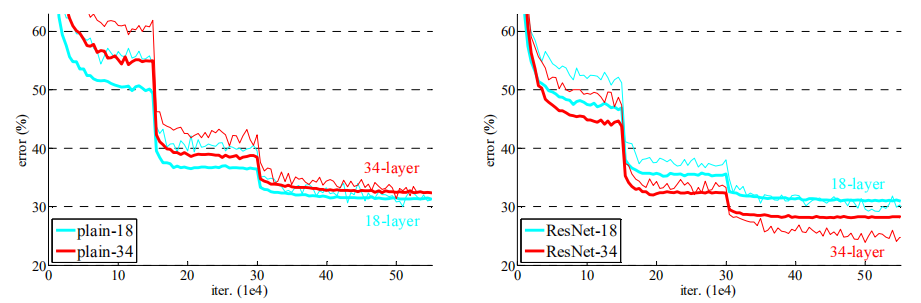
如果网络"并不是特别深"(如18层),现有的SGD能够很好的对普通网络进行求解,而ResNet能够使优化得到更快的收敛
恒等 vs 映射 Shortcuts
已经验证了无参数的恒等shortcuts是有助于训练的。接下来研究映射shortcut(Eq.2),比较了三种选项
- 对增加的维度使用0填充,所有的shortcuts是无参数的
- 对增加的维度使用映射shortcuts,其它使用恒等shortcuts
- 所有的都是映射shortcuts
实验表明三种选项的模型都比普通模型要好,2略好于1,研究者认为这是因为1中的0填充并没有进行残差学习。3略好于2,研究者将其归结于更多的(13个)映射shortcuts所引入的参数,实验结果也表明映射shortcuts对于解决退化问题并不是必需的,因此为了减少复杂度和模型尺寸,在之下的研究中并不使用模型3。恒等shortcuts因其无额外复杂度而对以下介绍的瓶颈结构尤为重要
深度瓶颈结构
将构建块修改为瓶颈设计。对于每一个残差函数\(F\),使用了三个叠加层而不是两个,这三层分别是1*1、3*3 和1*1 的卷积,1*1 的层主要负责减少然后增加(恢复)维度,剩下的3*3的层来减少输入和输出的维度
构建块(Fig.5),这两种设计具有相似的时间复杂度
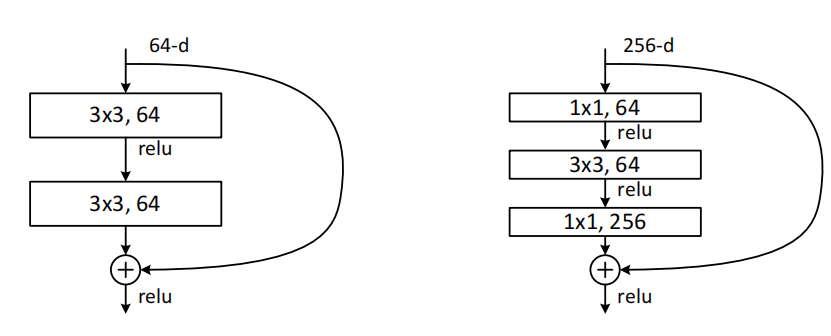
无参数的恒等shortcuts对于瓶颈结构尤为重要。如果使用映射shortcuts来替代Fig.5(右)中的恒等shortcuts,将会发现时间复杂度和模型尺寸都会增加一倍,因为shortcut连接了两个高维端,所以恒等shortcuts对于瓶颈设计是更加有效的
层响应分析
在CIFAR-10上层响应的标准方差(std)
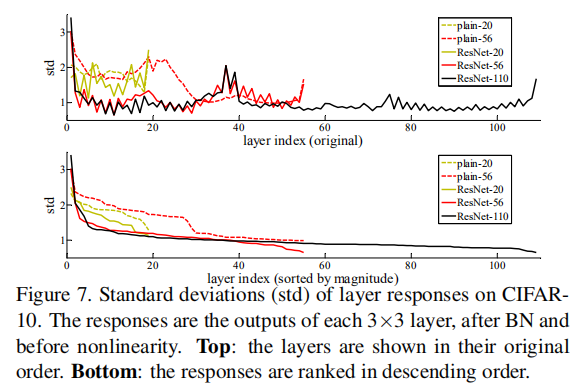
以标准方差来展示层响应,响应是每一个3*3卷积层的BN之后、非线性层(ReLU/addition)之前的输出,实验表明ResNets的响应比它对应的普通网络的响应要小,即残差函数比非残差函数更接近于0,同时越深的ResNet的响应幅度越小。当使用越多层时,ResNets中单个层对信号的改变越少
总结
网络随着深度的增加,训练误差和测试误差非但没有降低,反而变大了,然而这种问题的出现并不是因为过拟合,该现象被称为退化问题(degradation problem),本文即是为了解决深度神经网络中产生的退化问题
\(x\)作为我们的输入,期望的输出是\(H(x)\),如果我们直接把输入\(x\)传到输出作为初始结果,那么我们需要学习的目标就变成了\(F(X) = H(x) - x\)。Resnet相当于将学习目标改变了,不再是学习一个完整的输出\(H(x)\),而是\(H(x)-x\),即残差,进行这样的改变不会计算量和参数,却能使网络更容易优化。然后,ResNet就是在原来网络的基础上,每隔2层(或者3层,或者更多)的输出\(F(x)\)上再加上之前的输入\(x\)。这样做,整个网络就可以用SGD方法进行端对端的训练,用目前流行的深度学习库(caffe等)也可以很容易地实现
本文提出的深度残差学习架构,其中的构建块为
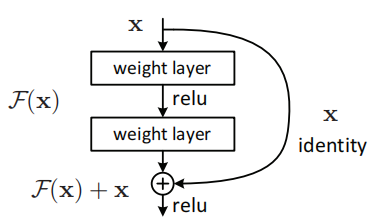
该结构的思想就是:如果增加的层能够改善恒等映射,更深的网络应该不会比对应的浅层网络的训练误差大。如果恒等映射是最优的,训练会驱使增加的非线性层的权重趋于0以靠近恒等映射
这种网络的优点有
- 更容易优化
- 网络越深,准确率越高
参考文献
[论文阅读] Deep Residual Learning for Image Recognition(ResNet)
Deep Residual Learning for Image Recognition(残差网络)
推荐阅读
对ResNet本质的一些思考




