直线与圆的最值问题（高二）
专题：直线+圆 \(\qquad \qquad\) 题型：最值问题 \(\qquad \qquad\) 难度系数：★★★
题目
已知\(P\)为圆\(C：x^2+y^2=1\)上的动点，直线\(l_1：kx-y-3k=0\)恒过定点\(A\)，\(Q\)为直线\(l_2：x-y+3=0\)上的动点，则\(|PA|+3|PQ|\)的最小值为 \(\underline{\quad \quad}\) .
思考痕迹
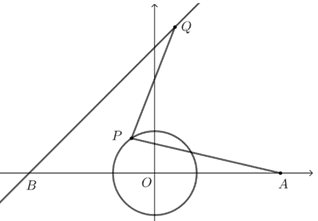
- 最值问题，常见方法就代数法和几何法；设元引入参数，把问题转化为函数问题，计算难度很大，故舍去；采取几何法；
- 几何法，脑子过下常见的几何模型：将军饮马、三点共线、垂线段最短、圆外点与圆上点的距离、胡不归等；
- 把\(|PA|+3|PQ|\)化为两条线段之和，可把\(|PA|+3|PQ|\)中的“\(3|PQ|\)”或\(\left|PA\right|+3\left|PQ\right|=3(\dfrac{1}{3}|PA|+|PQ|)\)中“\(\dfrac{1}{3}\left|PA\right|\)” 用一线段表示；
- 两动点问题，想化为一动点问题：先当动点\(P\)为一定点，确定动点\(Q\)什么情况下\(|PA|+3|PQ|\)最小值，再把点\(P\)动起来，操作起来行不通；
- 利用题中图象的对称性，看下能否得到\(|PB|\)与\(|PA|\)有无什么关系，貌似没有.
错解
基于以上几点，作了一些尝试.
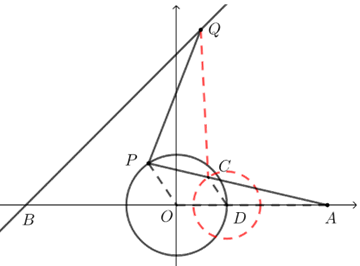
在线段\(PA\)上取点\(C\)，使得\(|PC|=\dfrac{1}{3}\left|PA\right|\)，
则\(\left|PA\right|+3\left|PQ\right|=3(\dfrac{1}{3}|PA|+|PQ|)=3|PC|+|PQ|≥3|CQ|\)①，
因为\(D(1,0)\)，\(A(3,0)\)，易得\(\left|CD\right|=\dfrac{1}{3}\left|OP\right|=\dfrac{1}{3}\)，
即点\(C\)在以点\(D\)为圆心，半径为\(\dfrac{1}{3}\)的圆上，
则\(\left|CQ\right|_{min}\)等于点\(D(1,0)\)到直线\(l_2：x-y+3=0\)的距离减去半径，即\(2\sqrt2-\dfrac{1}{3}\)；
则\(\left|PA\right|+3\left|PQ\right|\)的最小值\(6\sqrt2-1\).
错因分析
推导过程式子①中\(3|PC|+|PQ|≥3|CQ|\)，当\(C\)、\(P\)、\(Q\)三点共线时取到的；
而\(\left|CQ\right|_{min}\)是当\(DQ\bot\)直线\(l_2\)时取到的，
但它们不能同时取到，故答案不对.
详解
最后想到了“阿氏圆模型”
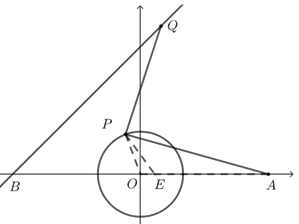
取点\(E(\dfrac{1}{3},0)\)，
因为\(\dfrac{\left|OE\right|}{\left|OP\right|}=\dfrac{\left|OP\right|}{\left|OA\right|}=\dfrac{1}{3}\)，且\(\angle POE=\angle AOP\)，所以\(∆POE \sim ∆AOP\)，
所以\(\left|PE\right|=\dfrac{1}{3}\left|PA\right|\).
则\(\left|PA\right|+3\left|PQ\right|=3(\dfrac{1}{3}|PA|+|PQ|)=3|PE|+|PQ|≥3|EQ|\)，
显然当\(EQ\bot\)直线\(l_2\)时，\(\left|EQ\right|\)取到最小值\(d=\dfrac{|\dfrac{1}{3}+3|}{\sqrt2}=\dfrac{5\sqrt2}{3}\)，
所以\(\left|PA\right|+3\left|PQ\right|\)的最小值为\(5\sqrt2\).
内容补充---阿氏圆
阿波罗尼斯圆定理
如图，\(P\)是平面上一动点，\(A\)、\(B\)是两定点，\(PA＝kPB(k>0\)且\(k\neq1)\)，则\(P\)点的轨迹是圆.
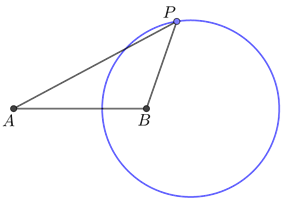
阿氏圆模型
“\(PA+k·PB\)”型最值问题.
当\(k=1\)时，即可转化为“\(PA+PB\)”之和最值问题，如 “将军饮马”模型.
当\(k\neq1\)时，常规的轴对称思想无法使用.因此我们想要通过转化，把题目变为我们熟悉的模型，在这个过程中产生了两种模型. 当动点P在直线上运动的类型称之为“胡不归”模型；点\(P\)在圆周上运动的类型称之为“阿氏圆”模型.
如下图，\(⊙O\)的半径为\(r\)，点\(A\)、\(B\)都在\(\odot O\)外，\(P\)是\(\odot O\)上一动点，已知\(r=k·OB\)， 连接\(PA\)、\(PB\)，则当“\(PA+k·PB\)”的值最小时，\(P\)点的位置如何确定？
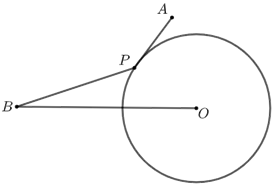
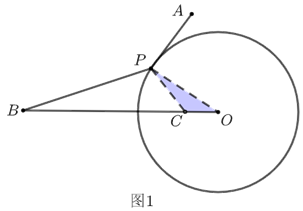
解析 如图1，在线段\(OB\)上截取\(OC\)使\(OC=k·OP\)，
则有\(\triangle BPO\)与\(\triangle PCO\)相似(利用对应边成比例)，由此可得\(k·PB=PC\)(转化成功).
故本题求“\(PA+k·PB\)”的最小值可以转化为“\(PA+PC\)”的最小值，
故当\(A\)、\(P\)、\(C\)三点共线时，“\(PA+PC\)”值最小.如图2.
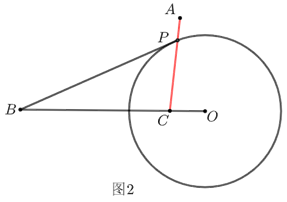
做题时最关键步骤就是“转化\(k·PB\)”，
即在\(OB\)上找到点\(C\)，使得\(\dfrac{OC}{OP}=\dfrac{OP}{OB}\).
