二次函数与圆的综合（初三）

专题：二次函数+圆 \(\qquad \qquad\) 题型：隐圆+轨迹 \(\qquad \qquad\) 难度系数：★★★★★
 

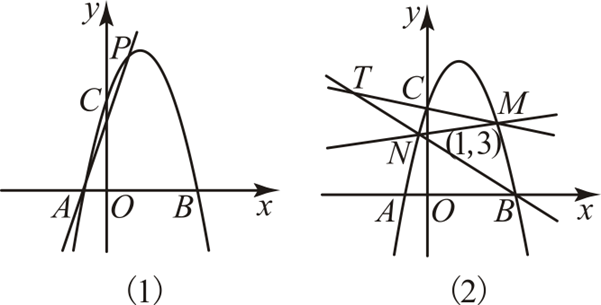
（2024年湖北模拟预测）如图，抛物线\(y=-x^2+3x+4\)与\(x\)轴分别交于\(A\)，\(B\)两点（点\(A\)在点\(B\)的左侧），与\(y\)轴交于点\(C\)．

(1)直接写出\(A\)，\(B\)，\(C\)三点的坐标；

(2)如图（1），\(P\)是抛物线上异于\(A\)，\(B\)的一点，将点\(B\)绕点\(P\)顺时针旋转\(45°\)得到点\(Q\)，若点\(Q\)恰好在直线上，求点\(P\)的坐标；

(3)如图（2），\(M\)，\(N\)是抛物线上异于\(B\)，\(C\)的两个动点，直线\(BN\)与直线\(CM\)交于点\(T\)，若直线\(MN\)经过定点\(\left(1,3\right)\)，求证：点\(T\)的运动轨迹是一条定直线．

 

【详解】
（1）解：对于抛物线\(y=-x^2+3x+4\)，当\(x=0\)时，\(y=4\)，则\(C\left(0,4\right)\)，

当\(y=0\)，即\(-x^2+3x+4=0\)，解得：\(x_1=-1\)，\(x_2=4\)\(∴ A\left(-1,0\right),B\left(4,0\right)\).
 

（2）解：

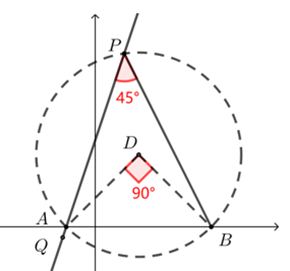
典型的“定弦定角的隐圆问题”，依题意可知，点\(P\)在以\(AB=5\)为弦，圆周角为\(\angle APB=45°\)的上，则点\(P\)为抛物线与\(\odot D\)的交点，即\(PD\)等于圆的半径.

如图所示，以\(AB\)为斜边向上作等腰直角三角形\(\triangle ABD\)，

\(∵A\left(-1,0\right),B\left(4,0\right)\)，则\(AB=5\)，\(∴x_D=\dfrac{-1+4}{2}=\dfrac{3}{5}\)，\(y_D=\dfrac{1}{2}AB=\dfrac{5}{2}\)，

\(∴D\left(\dfrac{3}{2},\dfrac{5}{2}\right)\)
确定圆心\(D\)坐标和求半径.

依题意，\(\angle APB=45° =\dfrac{1}{2}\angle ADB\)，

\(∴P\)是半径为\(\dfrac{5}{2}\sqrt2\)的\(\odot D\)与抛物线的交点，

设\(P\left(m,-m^2+3m+4\right)\)，其中\(-1<m<4\)，

\(∴\left(m-\dfrac{3}{2}\right)^2+\left(-m^2+3m+4-\dfrac{5}{2}\right)^2=\left(\dfrac{5}{2}\sqrt2\right)^2\)，

由\(PD=r=\dfrac{5}{2}\sqrt2\)，通过设元求点\(P\)坐标.

整理得\(\left(m+1\right)\left(m-4\right)\left(m-2\right)\left(m-1\right)=0\)，解得：\(m=\pm1,2,4\)，

\(∵-1<m<4\)，\(∴m=1\)或\(m=2\)，

则\(P\left(1,6\right)\)或\(P\left(2,6\right)\)；
 

（3）要点1：要证“点\(T\left(m,n\right)\)的运动轨迹是一条定直线”，即只需要证明\(m,n\)存在一次函数关系或\(m,n\)其中一个是定值．

要点2：要确定动点\(T\)的轨迹，需要了解它运动的源头和它是如何产生的；

方法1 ：逆向思考，动点\(T\)是直线\(NB\)和\(MC\)的交点，则可设法求出两条直线的方程，再联立便可知\(m,n\)的关系；

要求直线\(NB\)和\(MC\)方程，这可设点\(M(x_1,y_1)\)和\(N(x_2,y_2)\)，由直线\(MN\)联立抛物线可知\(x_1,y_1,\ x_2,y_2\)的关系；

\(x_1,y_1,\ x_2,y_2\)表示\(m,n\)便可得到\(m,n\)的关系，确定轨迹.

方法2 ：设点\(T\left(m,n\right)\)，由点\(T\)和点\(C\)得到直线\(MC\)的方程，由点\(T\)和点\(B\)得到直线\(NB\)的方程；

两条直线方程分别与抛物线联立方程得到点\(M，N\)的坐标；

再利用直线\(MN\)过点\((1,3)\)得到\(m,n\)的关系从而确定轨迹.

解：设\(T\left(m,n\right)\)，

\(∵B(4,0)\)，\(C\left(0,4\right)\)，

设直线\(TB,TC\)的解析式分别为\(y_1=k_1x+b_1\)，\(y_2=k_2x+b_2\)，

利用高中的直线的点斜式方程，求解会简单些.

\(\therefore\left\{\begin{array}{l} 4 k_1+b_1=0 \\ m k_1+b_1=n \end{array}\right.\)，\(\left\{\begin{array}{c} b_2=4 \\ m k_2+b_2=n \end{array}\right.\)，

解得：\(\left\{\begin{array}{l} k_1=\dfrac{n}{m-4} \\ b_2=\dfrac{4 n}{4-m} \end{array}\right.\)，\(\left\{\begin{array}{c} k_2=\dfrac{n-4}{m} \\ b_2=4 \end{array}\right.\)，

\(\therefore y_1=\dfrac{n}{m-4} x+\frac{4 n}{4-m}\)，\(y_2=\dfrac{n-4}{m} x+4\)

联立\(\left\{\begin{array}{l} y_1=\frac{n}{m-4} x+\frac{4 n}{4-m} \\ y=-x^2+3 x+4 \end{array}\right.\)，\(\left\{\begin{array}{c} y_2=\frac{n-4}{m} x+4 \\ y=-x^2+3 x+4 \end{array}\right.\)，

消去\(y\)得：\(x^2+\left(\dfrac{n}{m-4}-3\right) x-4+\dfrac{4 n}{4-m}=0\)，\(x^2+\left(\dfrac{n-4}{m}-3\right) x=0\)，

\(\therefore x_B+x_N=3-\dfrac{n}{m-4}\)，即\(x_N=-\dfrac{n}{m-4}-1\)，

由\(x^2+\left(\dfrac{n-4}{m}-3\right) x=0\)可得\(x_M=3-\dfrac{n-4}{m}\)，

两直线方程与抛物线联立，可求点\(M，N\)的坐标；而仅求它们横坐标会简单些，不要死求，注意到点\(B,C\)是定点，用韦达定理简单些.

依题意，直线\(MN\)的解析式为\(y=k(x-1)+3\)，即\(y=kx-k+3\)，

联立\(\left\{\begin{array}{c} y=k x-k+3 \\ y=-x^2+3 x+4 \end{array}\right.\)，则\(x^2+\left(k-3\right)x-\left(k+1\right)=0\)，

\(∴x_M+x_N=3-k\)，\(x_M\cdot x_N=-k-1\)，

利用韦达定理是常规手段.

\(\therefore\left\{\begin{array}{c} \left(-\dfrac{n}{m-4}-1\right)\left(3-\dfrac{n-4}{m}\right)=-k-1 \\ -\dfrac{n}{m-4}-1+3-\dfrac{n-4}{m}=3-k \end{array}\right.\)，

消去\(k\)得：\(\dfrac{n}{m-4}+\dfrac{n-4}{m}+1=\left(\dfrac{n}{m-4}+1\right)\left(3-\dfrac{n-4}{m}\right)-1\)，

解得：\(n=-m+4\)（与直线\(BC\)重合，故舍去）或\(n=m+8\).

即点\(T\)的运动轨迹是一条定直线\(y=x+8\)．

消参\(k\)得\(m,n\)的关系式，确定动点\(T\)的轨迹.