8.3 简单几何体的表面积和体积

$\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }$【高分突破系列】高一数学下学期同步知识点剖析精品讲义！
$\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}$

必修第二册同步拔高，难度3颗星！

模块导图

知识剖析

柱体

1 棱柱
体积：$V=Sh$(其中$h$是棱柱的高)

2 圆柱
(1) 侧面积：$S=2πrh$
(2) 全面积：$S=2πrh+2πr^2$
(3) 体积：$V=Sh=πr^2 h$ (其中$r$为底圆的半径，$h$为圆柱的高)

锥体

① 棱锥
棱锥体积：$V=\dfrac{1}{3} S h$(其中$h$为圆柱的高)；

② 圆锥
(1) 圆锥侧面积：$S=πrl$
(2) 圆锥全面积：$S=\pi r(r+l)$ (其中$r$为底圆的半径，$l$为圆锥母线)
(3) 圆锥体积：$V=\dfrac{1}{3} S h=\dfrac{1}{3} \pi r^{2} h$ (其中$r$为底圆的半径，$h$为圆柱的高)

台体

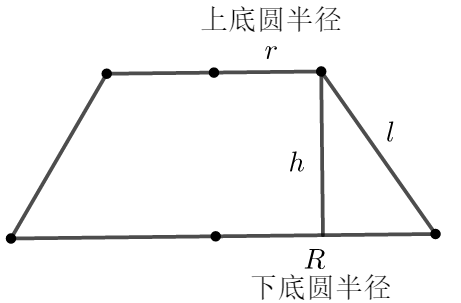
① 圆台表面积 $S=\pi\left({r^{\prime}}^{2}+r^{\prime 2}+r^{\prime} l+r l\right)$
其中是上底面圆的半径，$r$是下底面圆的半径，$l$是母线的长度.
② 台体体积 $V=\dfrac{1}{3}\left(S^{\prime}+\sqrt{S S^{\prime}}+S\right) h$
其中$S， S^{\prime}$分别为上，下底面面积，$h$为圆台的高.

球体

面积$S=4πR^2$，体积$V=\dfrac{4}{3} \pi R^{3}$ （其中$R$为球的半径）

经典例题

【题型一】几何体的表面积

【典题1】 已知正四棱柱$ABCD－A_1 B_1 C_1 D_1$中$AB=2$，$AA_1=3$，$O$为上底面中心．设正四棱柱$ABCD－A_1 B_1 C_1 D_1$与正四棱锥$O－A_1 B_1 C_1 D_1$的侧面积分别为$S_1$，$S_2$，则$\dfrac{S_{2}}{S_{1}}=$ $\underline{\quad \quad}$．

【解析】 如图，

正四棱柱$ABCD－A_1 B_1 C_1 D_1$中，$AB=2$，$AA_1=3$，
则正四棱柱$ABCD－A_1 B_1 C_1 D_1$的侧面积分别为$S_1=4×2×3=24$；
正四棱锥$O－A_1 B_1 C_1 D_1$的斜高为$\sqrt{1^{2}+3^{2}}=\sqrt{10}$．
$∴$正四棱锥$O－A_1 B_1 C_1 D_1$的侧面积$S_{2}=4 \times \dfrac{1}{2} \times 2 \times \sqrt{10}=4 \sqrt{10}$．
$\therefore \dfrac{S_{2}}{S_{1}}=\dfrac{4 \sqrt{10}}{24}=\dfrac{\sqrt{10}}{6}$．
【点拨】 注意侧面积和全面积的区别．

【典题2】 一个底面半径为$2$，高为$4$的圆锥中有一个内接圆柱，该圆柱侧面积的最大值为（　　）
A. $2 \pi$ $\qquad \qquad \qquad \qquad$ B. $\qquad \qquad \qquad \qquad$$4 \pi$ $\qquad \qquad \qquad \qquad$D. $5 \pi$
【解析】

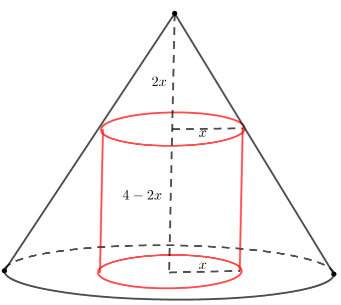
圆锥的底面半径为$2$，高为$4$，
$∴$内接圆柱的底面半径为$x$时，它的上底面截圆锥得小圆锥的高为$2x$
因此，内接圆柱的高 $h=4-2x$；
$∴$圆柱的侧面积为：$S=2 \pi x(4-2 x)=4 \pi\left(2 x-x^{2}\right) \quad(0<x<2)$
令$t=2x-x^2$，当$x=1$时$t_{\max }=1$；
所以当$x=1$时，$S_{\max }=4 \pi$．
即圆柱的底面半径为$1$时，圆柱的侧面积最大，最大值为$4π$．
故选：$C$．
【点拨】
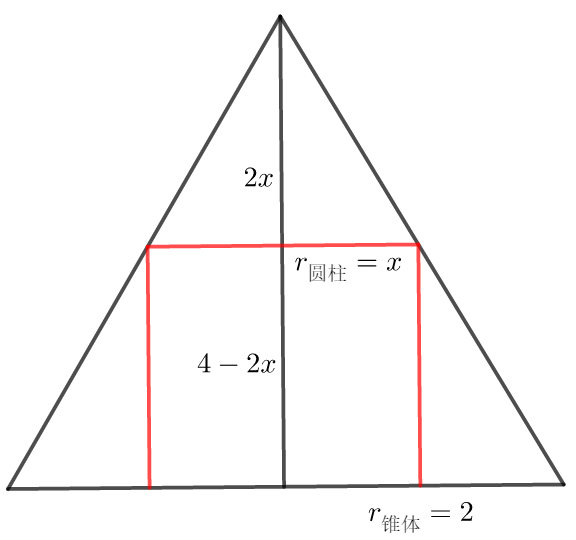
① 圆柱的侧面积$S=2πrh$，则需要知道圆柱的高$h$与底圆半径$r$；
② 在处理圆锥、圆柱问题时，要清楚母线、高、底圆的半径之间的关系，则要看轴截面(如下图)，此时由相似三角形的性质可以得到每个量的关系.

【典题3】 一个圆台上、下底面半径分别为$r$、$R$，高为$h$，若其侧面积等于两底面面积之和，则下列关系正确的是(　　)
A. $\dfrac{2}{h}=\dfrac{1}{R}+\dfrac{1}{r}$ $\qquad \qquad \qquad \qquad$ B. $\dfrac{1}{h}=\dfrac{1}{R}+\dfrac{1}{r}$
C. $\dfrac{1}{r}=\dfrac{1}{R}+\dfrac{1}{h}$ $\qquad \qquad \qquad \qquad$D. $\dfrac{2}{R}=\dfrac{1}{r}+\dfrac{1}{h}$
【解析】 设圆台的母线长为$l$，
根据题意可得圆台的上底面面积为$S_{\text {上 }}=\pi r^{2}$，圆台的下底面面积为$S_下=πR^2$，
$∵$圆台的侧面面积等于两底面面积之和，
$∴$侧面积$S_{\text {侧 }}=\pi\left(r^{2}+R^{2}\right)=\pi(r+R) l \text {， }$，解之得$l=\dfrac{r^{2}+R^{2}}{r+R}$
$\because l=\sqrt{h^{2}+(R-r)^{2}}$
$\therefore \dfrac{r^{2}+R^{2}}{r+R}=\sqrt{h^{2}+(R-r)^{2}}$，
$\therefore\left(\dfrac{r^{2}+R^{2}}{r+R}\right)^{2}=h^{2}+(R-r)^{2}$
$\therefore \dfrac{2}{h}=\dfrac{1}{R}+\dfrac{1}{r}$．故选 $A$．
【点拨】 在处理圆台问题时，要清楚母线、上底圆半径、下底圆半径、高之间的关系，则要看轴截面(如下图)，有$l=\sqrt{h^{2}+(R-r)^{2}}$.

【题型二】几何体的体积

【典题1】 正方形$ABCD$被对角线$BD$和以$A$为圆心，$AB$为半径的圆弧$\widehat{D B}$分成三部分，绕$AD$旋转，所得旋转体的体积$V_1$、$V_2$ 、$V_3$之比是(　　)

A. $ 2: 1: 1$ $\qquad \qquad \qquad$ B. $1: 2: 1$ $\qquad \qquad \qquad$C. $1: 1: 1$ $\qquad \qquad \qquad$ D. $2: 2: 1$
【解析】 设正方形$ABCD$的边长为$1$，可得
图$1$旋转所得旋转体为以$AD$为轴的圆锥体，高$AD=1$且底面半径$r=1$
$∴$该圆锥的体积为$V_{1}=\dfrac{1}{3} \pi \times A B^{2} \times A D=\dfrac{1}{3} \pi$；
图$2$旋转所得旋转体，是以$AD$为半径的一个半球，减去图$1$旋转所得圆锥体而形成，
∴该圆锥的体积为$V_{2}=V_{\text {半球 }}-V_{1}=\dfrac{1}{2} \times \dfrac{4}{3} \pi \times A D^{2}-V_{1}=\dfrac{1}{3} \pi$；
图$3$旋转所得旋转体，是以$AD$为轴的圆柱体，减去图$2$旋转所得半球而形成，
$∴$该圆锥的体积为$V_{3}=\pi \times A B^{2} \times A D-V_{\text {半球 }}=\pi-\dfrac{2}{3} \pi=\dfrac{1}{3} \pi$
综上所述$V_{1}=V_{2}=V_{3}=\dfrac{1}{3} \pi$，
由此可得图中$1、2、3$三部分旋转所得旋转体的体积之比为$1∶1∶1$．故选 $C$．
【点拨】
① 圆锥是由直角三角形以某一直角边为轴旋转得到；圆柱是由矩形以某一边为轴旋转得到；球是由半圆以直径为轴旋转得到;
② 求解不规则图形可用“割补法”.

【典题2】 如图，圆锥形容器的高为$h$，圆锥内水面的高为$h_1$，且$h_{1}=\dfrac{1}{3} h$，若将圆锥的倒置，水面高为$h_2$，则$h_2$等于(　　)

A. $\dfrac{2}{3} h$ $\qquad \qquad \qquad \qquad$B. $\dfrac{19}{27} h$ $\qquad \qquad \qquad \qquad$ C. $\dfrac{\sqrt[3]{6}}{3} h$ $\qquad \qquad \qquad \qquad$ D. $\dfrac{\sqrt[3]{19}}{3} h$
【解析】方法一设圆锥形容器的底面积为$S$，则未倒置前液面的面积为$\dfrac{4}{9} S$．
$∴$水的体积$V=\dfrac{1}{3} S h-\dfrac{1}{3} \times \dfrac{4}{9} S \times\left(h-h_{1}\right)=\dfrac{19}{81} S h$．
设倒置后液面面积为$S′$，则$\dfrac{S^{\prime}}{S}=\left(\dfrac{h_{2}}{h}\right)^{2}$，$\therefore S^{\prime}=\dfrac{S h_{2}^{2}}{h^{2}}$ ．
$∴$水的体积$V=\dfrac{1}{3} S^{\prime} h_{2}=\dfrac{S h_{2}^{3}}{3 h^{2}}$．
$\therefore \dfrac{19}{81} S h=\dfrac{S h_{2}^{3}}{3 h^{2}}$，解得$h_{2}=\dfrac{\sqrt[3]{19} h}{3}$．
故选$D$．
方法二设容器为圆锥$1$，高为$h$，体积为$V$;倒置前液面上的锥体为圆锥$2$，高为$h^{\prime}=h-h_{1}$，体积为$V_1$；倒置后液面以下的锥体为圆锥$3$，高为$h_2$，体积为$V_2$.
$\because \dfrac{h_{1}}{h}=\dfrac{1}{3}$ $\therefore \dfrac{h^{\prime}}{h}=\dfrac{2}{3}$
$\therefore \dfrac{V-V_{\text {水 }}}{V}=\left(\dfrac{2}{3}\right)^{3}=\dfrac{8}{27} \Rightarrow \dfrac{V_{\text {水 }}}{V}=\dfrac{19}{27}，$，
在倒置后，又有$\dfrac{V_{\text {水 }}}{V}=\left(\dfrac{h_{2}}{h}\right)^{3}$ ，
$\therefore\left(\dfrac{h_{2}}{h}\right)^{3}=\dfrac{19}{27} \Rightarrow h_{2}=\dfrac{\sqrt[3]{19} h}{3}$.
【点拨】
① 涉及圆台的表面积和体积，可把圆台补全为圆锥；

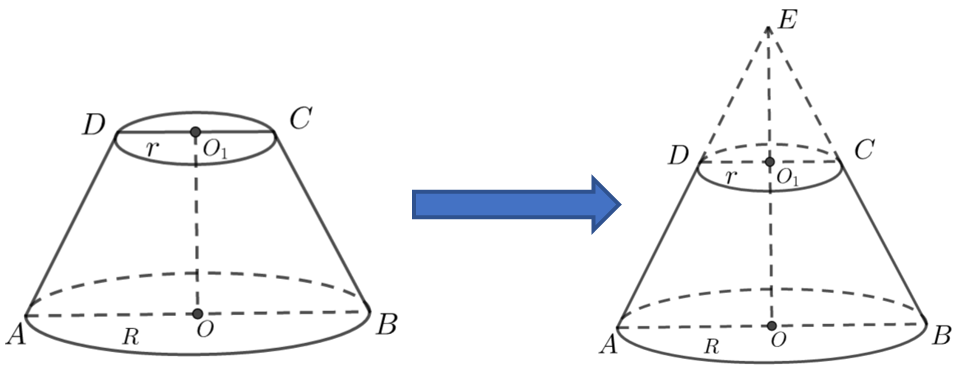
② 两个相似几何体，若相似比为$a$，则对应线段比为$a$，对应的平面面积比为$a^2$，对应的几何体体积比是$a^3$.

【典题3】 已知球的直径$SC=4$，$A$，$B$是该球球面上的两点，$AB=2$，$∠ ASC=∠BSC=45°$，则棱锥$S-ABC$的体积$V=$ $\underline{\quad \quad}$ .
【解析】 由题可知$AB$一定在与直径$SC$垂直的小圆面上，作过$AB$的小圆交直径$SC$于$D$，
如图所示，

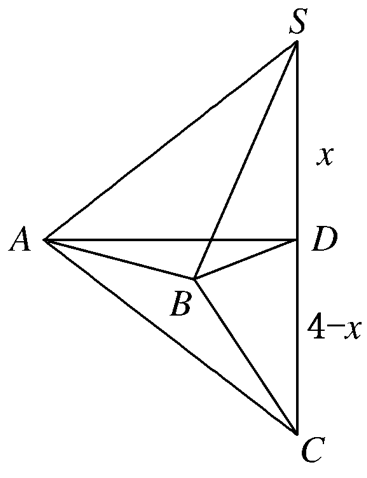
设$SD=x$，则$DC=4－x$，
此时所求棱锥即分割成两个棱锥$S-A B D$和$C-A B D$，
在$△SAD$和$△SBD$中，由已知条件可得$AD=BD=x$，
又因为$SC$为直径，所以$∠SBC=∠SAC=90°$，
所以$∠DBC=∠DAC=45°$，
所以在$△BDC$中，$BD=4－x$，
所以$x=4－x$，解得$x=2$，所以$AD=BD=2$，
所以$\triangle A B D$为正三角形，
所以$V=\dfrac{1}{3} S_{\triangle A B D} \times 4=\dfrac{4 \sqrt{3}}{3}$.
【点拨】
① 圆内直径所对的圆周角为$90°$；
② 若垂直于三棱锥的某棱长的截面面积为$S$，棱长长$h$，则三棱锥的体积为$\dfrac{1}{3} S h$．

【题型三】与球有关的切、接问题

【典题1】 已知三棱锥$D-ABC$的四个顶点在球$O$的球面上，若$AB=AC=BC=DB=DC=1$，当三棱锥$D－ABC$的体积取到最大值时，球$O$的表面积为（　　）
A. $\dfrac{5 \pi}{3}$ $\qquad \qquad \qquad \qquad$B. $2 \pi$ $\qquad \qquad \qquad \qquad$C. $5 \pi$ $\qquad \qquad \qquad \qquad$ D. $\dfrac{20 \pi}{3}$
【解析】 　如图，当三棱锥$D-ABC$的体积取到最大值时，则平面$ABC⊥$平面$DBC$，取$BC$的中点$G$，连接$AG$，$DG$，则$AG⊥BC$，$DG⊥BC$，分别取$△ABC$与$△DBC$的外心$E$，$F$，分别过$E$，$F$作平面$ABC$与平面$DBC$的垂线，相交于$O$，则$O$为四面体$ABCD$的球心，由$AB=AC=BC$$=DB=DC=1$，得正方形$OEGF$的边长为$\dfrac{\sqrt{3}}{6}$，则$O G=\dfrac{\sqrt{6}}{6}$
$∴$四面体$A-BCD$的外接球的半径$R=\sqrt{O G^{2}+B G^{2}}=\sqrt{\left(\dfrac{\sqrt{6}}{6}\right)^{2}+\left(\dfrac{1}{2}\right)^{2}}=\sqrt{\dfrac{5}{12}}$
$∴$球$O$的表面积为$=4 \pi \times\left(\sqrt{\dfrac{5}{12}}\right)^{2}=\dfrac{5 \pi}{3}$，故选：$A$．

【典题2】 如图，在一个底面边长为$2$，侧棱长为$\sqrt{10}$的正四棱锥$P－ABCD$中，大球$O_1$内切于该四棱锥，小球$O_2$与大球$O_1$及四棱锥的四个侧面相切，则小球$O_2$的体积为$\underline{\quad \quad}$．

【解析】 设$O$为正方形$ABCD$的中心，$AB$的中点为$M$，连接$PM$，$OM$，$PO$，则$OM=1$，$P M=\sqrt{P A^{2}-A M^{2}}=\sqrt{10-1}=3$，$P O=\sqrt{9-1}=2 \sqrt{2}$，
如图，在截面$PMO$中，设$N$为球$O_1$与平面$PAB$的切点，

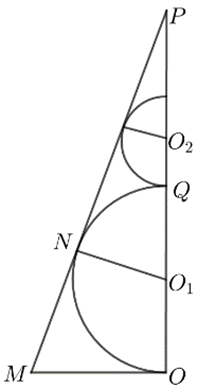
则$N$在$PM$上，且$O_1 N⊥PM$，设球$O_1$的半径为$R$，则$O_1 N=R$，
因为$\sin \angle M P O=\dfrac{O M}{P M}=\dfrac{1}{3}$，
所以$\dfrac{N O_{1}}{P O_{1}}=\dfrac{1}{3}$，则$PO_1=3R$，$P O=P O_{1}+O O_{1}=4 R=2 \sqrt{2}$，
所以$R=\dfrac{\sqrt{2}}{2}$，
设球$O_1$与球$O_2$相切与点$Q$，
则$PQ=PO－2R=2R$，设球$O_2$的半径为$r$，
同理可得$PQ=4r$，所以$r=\dfrac{R}{2}=\dfrac{\sqrt{2}}{4}$，
故小球$O_2$的体积$V=\dfrac{4}{3} \pi r^{3}=\dfrac{\sqrt{2}}{24} \pi$，
故答案为 $\dfrac{\sqrt{2}}{24} \pi$．

巩固练习

1(★) 如图$1$所示，一只封闭的圆柱形水桶内盛了半桶水(桶的厚度忽略不计)，圆柱形水桶的底面直径与母线长相等，现将该水桶水平放置后如图$2$所示，设图$1$、图$2$中水所形成的几何体的表面积分别为$S_1$ 、$S_2$，则$S_1$与$S_2$的大小关系是(　　)

A．$S_1≤S_2$ $\qquad \qquad \qquad$ B．$S_1 <S_2$ $\qquad \qquad \qquad$ C．$S_1>S_2$ $\qquad \qquad \qquad$ D．$S_1≥S_2$

2(★) 若一个圆锥的母线长为$4$，且其侧面积为其轴截面面积的$4$倍，则该圆锥的高为(　　)
A. $\pi$ $\qquad \qquad \qquad \qquad$ B. $\dfrac{3 \pi}{2}$ $\qquad \qquad \qquad \qquad$ C. $\dfrac{2 \pi}{3}$ $\qquad \qquad \qquad \qquad$ D. $\dfrac{\pi}{2}$

3(★★) 某广场设置了一些石凳供大家休息，这些石凳是由正方体截去八个一样大的四面体得到的(如图)．则该几何体共有$\underline{\quad \quad}$个面；如果被截正方体的棱长是$50cm$，那么石凳的表面积是$\underline{\quad \quad}$$cm^2$．

4(★★) 直角梯形的上、下底和不垂直于底的腰的长度之比为$12 \sqrt{3}$，那么以垂直于底的腰所在的直线为轴，将梯形旋转一周，所得的圆台上、下底面积和侧面面积之比是$\underline{\quad \quad}$ .

5(★★) 如图，四面体各个面都是边长为$1$的正三角形，其三个顶点在一个圆柱的下底面圆周上，另一个顶点是上底面圆心，圆柱的侧面积是$\underline{\quad \quad}$.

6(★★) 一竖立在地面上的圆锥形物体的母线长为$4m$，侧面展开图的圆心角为$\dfrac{2 \pi}{3}$，则这个圆锥的体积等于$\underline{\quad \quad}$.

7(★★) 如图①，一个圆锥形容器的高为$a$，内装有一定量的水．如果将容器倒置，这时所形成的圆锥的高恰为$\dfrac{a}{2}$(如图②)，则图①中的水面高度为$\underline{\quad \quad}$ .

8(★★★) 半径为$2$的球$O$内有一个内接正三棱柱，则正三棱柱的侧面积的最大值为$\underline{\quad \quad}$.

9(★★★) 如图所示，在边长为$5+\sqrt{2}$的正方形$ABCD$中，以$A$为圆心画一个扇形，以$O$为圆心画一个圆，$M$、$N$，$K$为切点，以扇形为圆锥的侧面，以圆$O$为圆锥底面，围成一个圆锥，则圆锥的全面积与体积分别是$\underline{\quad \quad}$与$\underline{\quad \quad}$．

10(★★★) 已知四面体$ABCD$的棱长满足$AB=AC=BD=CD=2$，$BC=AD=1$，现将四面体$ABCD$放入一个主视图为等边三角形的圆锥中，使得四面体$ABCD$可以在圆锥中任意转动，则圆锥侧面积的最小值为$\underline{\quad \quad}$．

11(★★★) 在直三棱柱$ABC－A_1 B_1 C_1$中，平面$ABC$是下底面．$M$是$BB_1$上的点，$AB=3$，$BC=4$，$AC=5$，$CC_1=7$，过三点$A$、$M$、$C_1$作截面，当截面周长最小时，截面将三棱柱分成的上、下两部分的体积比为$\underline{\quad \quad}$ .

12(★★★) 如图，在直三棱柱$ABC－A_1 B_1 C_1$中，$AB=1$，$BC=2$，$BB_1=3$，$∠ABC=90°$，点$D$为侧棱$BB_1$上的动点，当$AD+DC_1$最小时，三棱锥$D－ABC_1$的体积为$\underline{\quad \quad}$．

13(★★★) 已知$△SAB$是边长为$2$的等边三角形，$∠ACB=45°$，当三棱锥$S－ABC$体积最大时，其外接球的表面积为$\underline{\quad \quad}$ .

14(★★★) 如图，在$△ABC$中，$AB=BC=2$，$∠ABC=120°$．若平面$ABC$外的点$P$和线段$AC$上的点$D$，满足$PD=DA$，$PB=BA$，则四面体$PBCD$的体积的最大值是$\underline{\quad \quad}$．

参考答案

【答案】 $B$
【解析】 设圆柱的底面半径为$r$，图$1$水的表面积为$S_1=2πr^2+2πr\cdot r=4πr^2$．
对于图$2$，
上面的矩形的面积的长是$2r$，宽是$2r$．则面积是$4r^2$．
曲面展开后的矩形长是$πr$，宽是$2r$．则面积是$2πr^2$．
上下底面的面积的和是$π×r^2$．
图$2$水的表面积$S_2=(4+3π) r^2$．
显然$S_1 <S_2$．
故选$B$．
【答案】 $A$
【解析】 设圆锥的底面圆半径为$r$，高为$h$；
由圆锥的母线长为$4$，所以圆锥的侧面积为$\pi r \cdot 4=4 \pi r$；
又圆锥的轴截面面积为$\dfrac{1}{2} \cdot 2 r \cdot h=r h$，
所以$4πr=4rh$，解得$h=π$；
所以该圆锥的高为$π$．
故选：$A$．
【答案】 $14$，$10000$
【解析】 由题意知，截去的八个四面体是全等的正三棱锥，$8$个底面三角形，再加上$6$个小正方形，所以该几何体共有$14$个面；
如果被截正方体的棱长是$50cm$，那么石凳的表面积是
$S_{\text {表面积 }}=8 \times \dfrac{1}{2} \times 25 \sqrt{2} \times 25 \sqrt{2} \times \sin 60^{\circ}$$+6 \times 25 \sqrt{2} \times 25 \sqrt{2}=10000\left(\mathrm{~cm}^{2}\right)$．
故答案为：$14$，$10000$．
【答案】 $1: 4: 3 \sqrt{3}$
【解析】 由题意可设直角梯形上底、下底和不垂直于底的腰为$x， 2 x， \sqrt{3} x$；
则圆台的上、下底半径和母线长分别为$x， 2 x， \sqrt{3} x$，如图所示；

所以上底面的面积为$S_{\text {上底 }}=\pi \cdot x^{2}$；下底面的面积为$S_{\text {下底 }}=\pi \cdot(2 x)^{2}=4 \pi x^{2}$；
侧面积为$S_{\text {侧面 }}=\pi(x+2 x) \cdot \sqrt{3} x=3 \sqrt{3} \pi x^{2}$；
所以圆台的上底、下底面积和侧面面积之比是$\pi x^{2}: 4 \pi x^{2}: 3 \sqrt{3} \pi x^{2}=1: 4: 3 \sqrt{3}$．
【答案】 $\dfrac{2 \sqrt{2} \pi}{3}$
【解析】 如图所示，过点$P$作$PE⊥$平面$ABC$，$E$为垂足，点$E$为的等边三角形$ABC$的中心．
$A E=\dfrac{2}{3} A D$，$A D=\dfrac{\sqrt{3}}{2}$．
$\therefore A E=\dfrac{2}{3} \times \dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{3}}{3}$．
$\therefore P E=\sqrt{P A^{2}-A E^{2}}=\dfrac{\sqrt{6}}{3}$．
设圆柱底面半径为$R$，则$2 R=\dfrac{1}{\sin 60^{\circ}}=\dfrac{2}{\sqrt{3}}$，
$∴$圆柱的侧面积$=2 \pi R \cdot P E=\dfrac{2}{\sqrt{3}} \pi \times \dfrac{\sqrt{6}}{3}=\dfrac{2 \sqrt{2} \pi}{3}$，
【答案】 $\dfrac{128 \sqrt{2}}{81} \pi m^{3}$
【解析】 设圆锥的底面半径为$r$，
圆锥形物体的母线长$l=4m$，侧面展开图的圆心角为$\dfrac{2 \pi}{3}$，
故$2 \pi r=\dfrac{2 \pi}{3}$，解得$r=\dfrac{4}{3} m$，
故圆锥的高$h=\sqrt{l^{2}-r^{2}}=\dfrac{8}{3} \sqrt{2} m$，
故圆锥的体积$V=\dfrac{1}{3} \pi r^{2} h=\dfrac{128 \sqrt{2}}{81} \pi m^{3}$．
【答案】 $\left(1-\dfrac{\sqrt[3]{7}}{2}\right) a$
【解析】 令圆锥倒置时水的体积为$V′$，圆锥体积为$V$，
则$\dfrac{V^{\prime}}{V}=\left(\dfrac{a}{2}\right)^{3} \div a^{3}=\dfrac{1}{8}$，$\therefore \dfrac{V_{\text {空 }}}{V_{\text {锥 }}}=\dfrac{7}{8}$，倒置后$V_{\text {水 }}=\dfrac{1}{8} V$，
设此时水高为$h$，则$h^{3} a^{3}=\dfrac{7}{8}$，$\therefore h=\left(1-\dfrac{\sqrt[3]{7}}{2}\right) a$．
故原来水面的高度为$\left(1-\dfrac{\sqrt[3]{7}}{2}\right) a$．
【答案】 $12 \sqrt{3}$
【解析】 如图所示，设正三棱柱上下底面的中心分别为$O_1$，$O_2$，底面边长与高分别为$x$，$h$，
则$O_{2} A=\dfrac{\sqrt{3}}{3} x$，在$Rt△OAO_2$中，$\dfrac{h^{2}}{4}+\dfrac{x^{2}}{3}=4$，
化为$h^{2}=16-\dfrac{4}{3} x^{2}$，
$\because S_{\text {侧 }}=3 x h$，$\therefore S_{\text {侧 }^{2}}^{2}=9 x^{2} h^{2}=12 x^{2}\left(12-x^{2}\right) \leq 12\left(\dfrac{x^{2}+12-x^{2}}{2}\right)^{2}=432$．
当且仅当$x^2=12－x^2$，即$x=\sqrt{6}$时取等号，
此时$S_{\text {侧 }}=12 \sqrt{3}$．
【答案】 $10 \pi， \dfrac{2 \sqrt{30}}{3} \pi$
【解析】 设圆锥的母线长为$l$，底面半径为$r$，高为$h$，

由已知条件可得$\left\{\begin{array}{l} l+r+\sqrt{2} r=(5+\sqrt{2}) \times \sqrt{2} \\ \dfrac{2 \pi r}{l}=\dfrac{\pi}{2} \end{array}\right.$，
解得$r=\sqrt{2}$，$l=4 \sqrt{2}$，
$\therefore S=\pi r l+\pi r^{2}=10 \pi$，
又$\because h=\sqrt{l^{2}-r^{2}}=\sqrt{30}$，$\therefore V=\dfrac{1}{3} \pi r^{2} h=\dfrac{2 \sqrt{30}}{3} \pi$．
故答案为$10 \pi， \dfrac{2 \sqrt{30}}{3} \pi$
【答案】 $\dfrac{27 \pi}{4}$
【解析】 因为四面体$ABCD$的棱长满足$AB=AC=BD=CD=2$，$BC=AD=1$，所以可以把其放到长宽高分别为$a$，$b$，$c$的长方体中，四面体的棱长是长方体的面对角线，
$∴a^2+b^2=2^2$，①；$b^2+c^2=2^2$，②；$c^2+a^2=1^2$，③
故四面体的外接球半径R满足：$8R^2=2^2+2^2+1^2=9$；
$\therefore R^{2}=\dfrac{9}{8}$．
$∵$四面体$ABCD$放入一个主视图为等边三角形的圆锥中，
使得四面体$ABCD$可以在圆锥中任意转动，
要想圆锥的侧面积最小；
故需满足四面体的外接球恰好是圆锥的内切球；
作圆锥的轴截面，如图：设$BE=r$，则$AB=2r$，$A E=\sqrt{3} r$；
可得：$OB^2=OE^2+EB^2$；
$\therefore R^{2}=(\sqrt{3} r-R)^{2}+r^{2} \Rightarrow r=\sqrt{3} R$；
故圆锥侧面积的最小值为：$\pi r l=2 \pi r^{2}=2 \pi \cdot 3 R^{2}=\dfrac{27 \pi}{4}$．
故答案为：$\dfrac{27 \pi}{4}$．
　
11 【答案】 $\dfrac{11}{10}$
【解析】 由$AB=3$，$BC=4$，$AC=5$，得$AB^2+BC^2=AC^2$，$∴AB⊥BC$．
将平面$ABB_1 A_1$ 与平面$BCC_1 B_1$放在一个平面内，
连接$AC_1$，与$BB_1$的交点即为$M$，此时$BM=3$，
设四棱锥$A－BCC_1M$的体积为$V_1$，
则$V_{1}=\dfrac{1}{3} \times \dfrac{1}{2} \times(3+7) \times 4 \times 3=20$，
三棱柱$ABC－A_1 B_1 C_1$的体积$V=\dfrac{1}{2} \times 4 \times 3 \times 7=42$．
$∴$当截面周长最小时，截面将三棱柱分成的上、下两部分的体积比为$\dfrac{V-V_{1}}{V_{1}}=\dfrac{11}{10}$．

12【答案】 $\dfrac{1}{3}$
【解析】 将直三棱柱$ABC－A_1 B_1 C_1$展开成矩形$ACC_1 A_1$，如图，
连结$AC_1$，交$BB_1$于$D$，此时$AD+DC_1$最小，
$∵AB=1$，$BC=2$，$BB_1=3$，$∠ABC=90°$，点$D$为侧棱$BB_1$上的动点，
$∴$当$AD+DC_1$最小时，$BD=1$，
此时三棱锥$D－ABC_1$的体积
$V_{D-A B C_{1}}=V_{C_{1}-A B D}=\dfrac{1}{3} \times S_{\triangle A B D} \times B_{1} C_{1}$
$=\dfrac{1}{3} \times \dfrac{1}{2} \times A B \times B D \times B_{1} C_{1}$$=\dfrac{1}{3} \times \dfrac{1}{2} \times 1 \times 1 \times 2=\dfrac{1}{3}$．

13 【答案】 $\dfrac{28 \pi}{3}$
【解析】 由题可知，平面$CAB⊥$平面$SAB$，且$CA=CB$时，三棱锥$S－ABC$体积达到最大，如右图所示，

则点$D$，点$E$分别为$△ASB$，$△ACB$的外心，并过两个三角形的外心作所在三角形面的垂线，两垂直交于点$O$．
$∴$点$O$是此三棱锥外接球的球心，$AO$即为球的半径．
在$△ACB$中，$AB=2$，$∠ACB=45°⇒∠AEB=90°$，
由正弦定理可知，$\dfrac{A B}{\sin \angle A C B}=2 A E$，$\therefore A E=E B=E C=\sqrt{2}$，
延长$CE$交$AB$于点$F$，延长$SD$交$AB$于点$F$，
$∴$四边形$EFDO$是矩形，且$OE⊥$平面$ACB$，则有$OE⊥AE$，
又∵OE=DF=1/3 SF=1/3×√3/2 AB=√3/3，
$\therefore O A=\sqrt{O E^{2}+A E^{2}}=\sqrt{\dfrac{7}{3}}$．
$\therefore S_{\text {球表面积 }}=4 \pi R^{2}=4 \pi \times\left(\sqrt{\dfrac{7}{3}}\right)^{2}=\dfrac{28 \pi}{3}$．
14 【答案】 $\dfrac{1}{2}$
【解析】 如图，$M$是$AC$的中点．
①当$A D=t<A M=\sqrt{3}$时，如图，此时高为$P$到$BD$的距离，也就是$A$到$BD$的距离，即图中$AE$，

$D M=\sqrt{3}-t$，由$\triangle A D E \backsim \triangle B D M$，
可得$\dfrac{h}{1}=\dfrac{t}{\sqrt{(\sqrt{3}-t)^{2}+1}}$，$\therefore h=\dfrac{t}{\sqrt{(\sqrt{3}-t)^{2}+1}}$，
$V=\dfrac{1}{3} \cdot \dfrac{1}{2} \cdot(2 \sqrt{3}-t) \cdot 1 \cdot \dfrac{t}{\sqrt{(\sqrt{3}-t)^{2}+1}}$$=\dfrac{1}{6} \cdot \dfrac{3-(\sqrt{3}-t)^{2}}{\sqrt{(\sqrt{3}-t)^{2}+1}}， \quad t \in(0， \sqrt{3})$
②当$A D=t>A M=\sqrt{3}$时，如图，此时高为$P$到$BD$的距离，也就是$A$到$BD$的距离，即图中$AH$，

$D M=t-\sqrt{3}$，由等面积，可得$\dfrac{1}{2} \cdot A D \cdot B M=\dfrac{1}{2} \cdot B D \cdot A H$，
$\therefore \dfrac{1}{2} \cdot t \cdot 1=\dfrac{1}{2} \sqrt{(t-\sqrt{3})^{2}+1}$，
$\therefore h=\dfrac{t}{\sqrt{(\sqrt{3}-t)^{2}+1}}$，
$\therefore V=\dfrac{1}{3} \cdot \dfrac{1}{2} \cdot(2 \sqrt{3}-t) \cdot 1 \cdot \dfrac{t}{\sqrt{(\sqrt{3}-t)^{2}+1}}$$=\dfrac{1}{6} \cdot \dfrac{3-(\sqrt{3}-t)^{2}}{\sqrt{(\sqrt{3}-t)^{2}+1}}， \quad t \in(\sqrt{3}， 2 \sqrt{3})$
综上所述，$V=\dfrac{1}{6} \cdot \dfrac{3-(\sqrt{3}-t)^{2}}{\sqrt{(\sqrt{3}-t)^{2}+1}}， \quad t \in(0，2 \sqrt{3})$
令$m=\sqrt{(\sqrt{3}-t)^{2}+1} \in[1，2)$，则$V=\dfrac{1}{6} \cdot \dfrac{4-m^{2}}{m}$
$∴m=1$时，$V_{\max }=\dfrac{1}{2}$．
故答案为$\dfrac{1}{2}$．