8.1-8.2 空间几何体的结构特征、直观图
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高一数学下学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
必修第二册同步拔高,难度3颗星!
模块导图
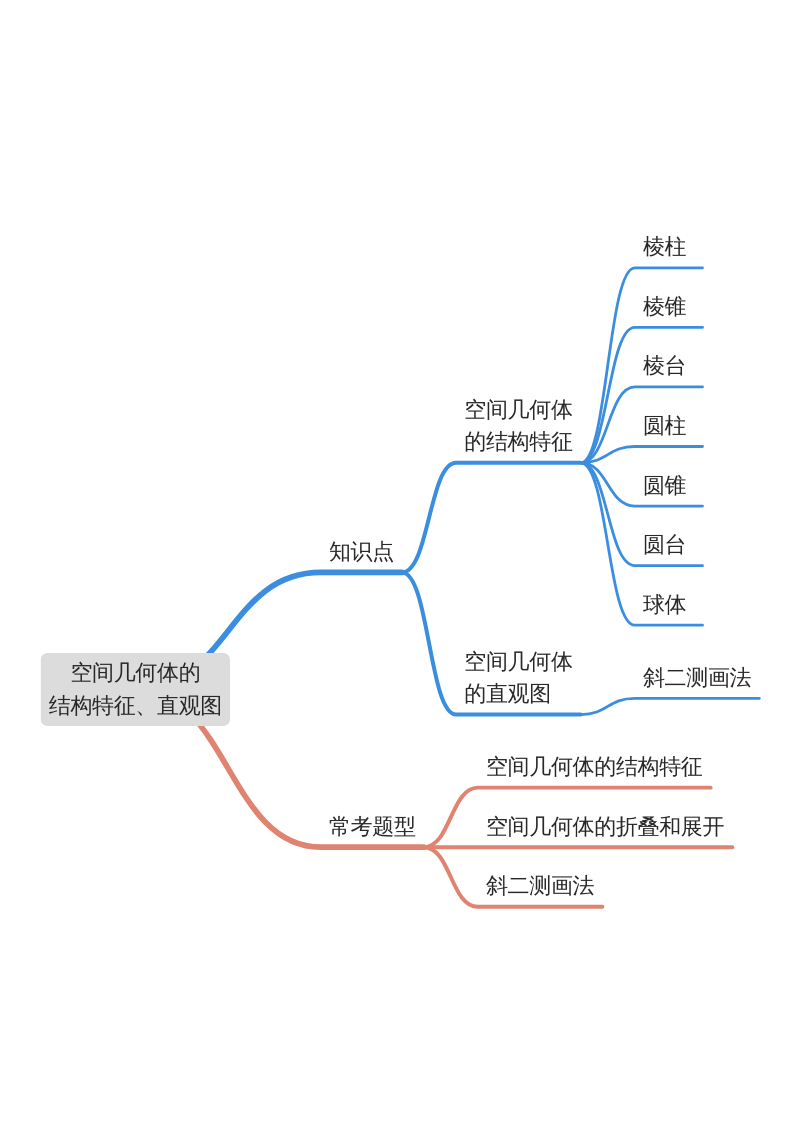
知识剖析
空间几何体的结构特征
1 空间几何体
多面体 由若干个平面多边形围成的几何体;
旋转体 由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体.
2 棱柱
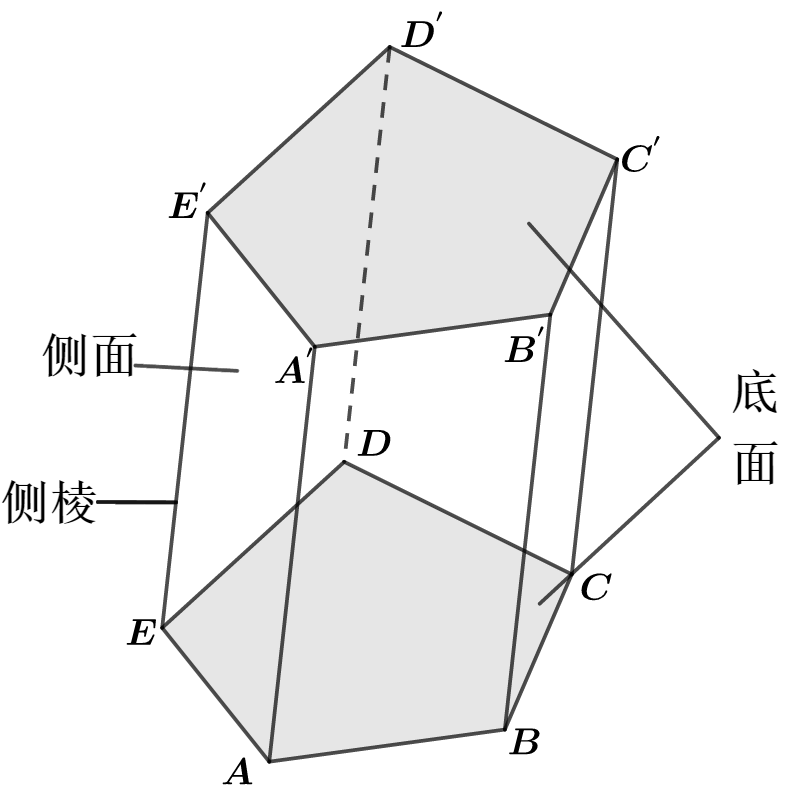
(1)概念
有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱.
(2)性质
① 侧棱都相等,侧面是平行四边形;
② 两个底面与平行于底面的截面是全等的多边形;
③ 过不相邻的两条侧棱的截面是平行四边形;
④ 直棱柱的侧棱长与高相等,侧面与对角面是矩形.
(3)分类
① 按底面多边形的边数分为:三棱柱,四棱柱等.
② 按侧棱是否垂直低面分为斜棱柱,直棱柱(底面是正多边形的直棱柱,叫正棱柱;底面是平行四边形的四棱柱也叫做平行六面体)
3 棱锥
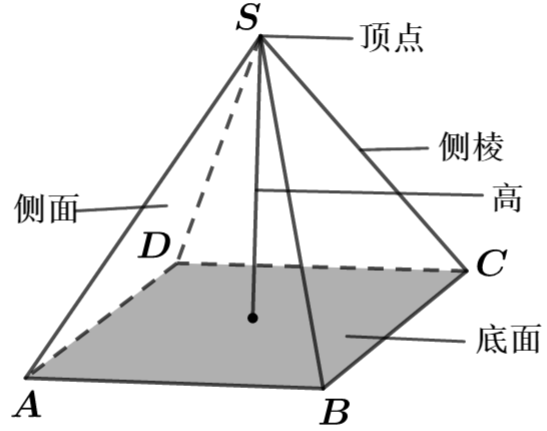
(1)概念
有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥.
如果有一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥.
(2)性质
① 平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的距离与顶点到底面的距离之比;
② 正棱锥各侧棱相等,各侧面是全等的等腰三角形;
③ 正棱锥中六个元素,即侧棱、高、斜高、侧棱在底面内的射影、斜高在底面的射影、底面边长一半,构成四个直角三角形.)
(3)常见棱锥
① 正三棱锥是底面是等边三角形,三个侧面是全等的等腰三角形的三棱锥.
② 正四面体是每个面都是全等的等边三角形的三棱锥,正四面体是特殊的正三棱锥.
** (4)侧面展开图**
正\(n\)棱锥的侧面展开图是有\(n\)个全等的等腰三角形组成的.
4 棱台
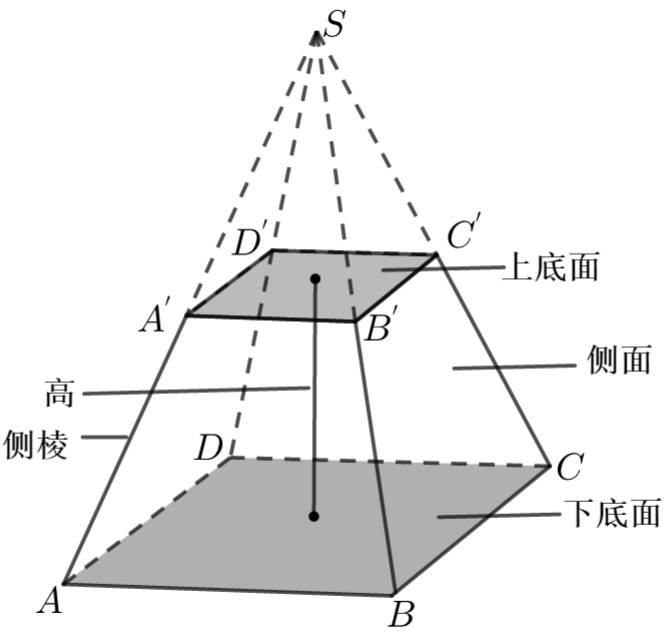
(1)用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台.
(2)棱台的分类:由三棱锥、四棱锥……截得的棱台分别叫做三棱台、四棱台…….
(3)正棱台:由正棱锥截得的棱台叫做正棱台,正棱台各侧棱都相等,各侧面都是全等的等腰梯形.
5 圆柱
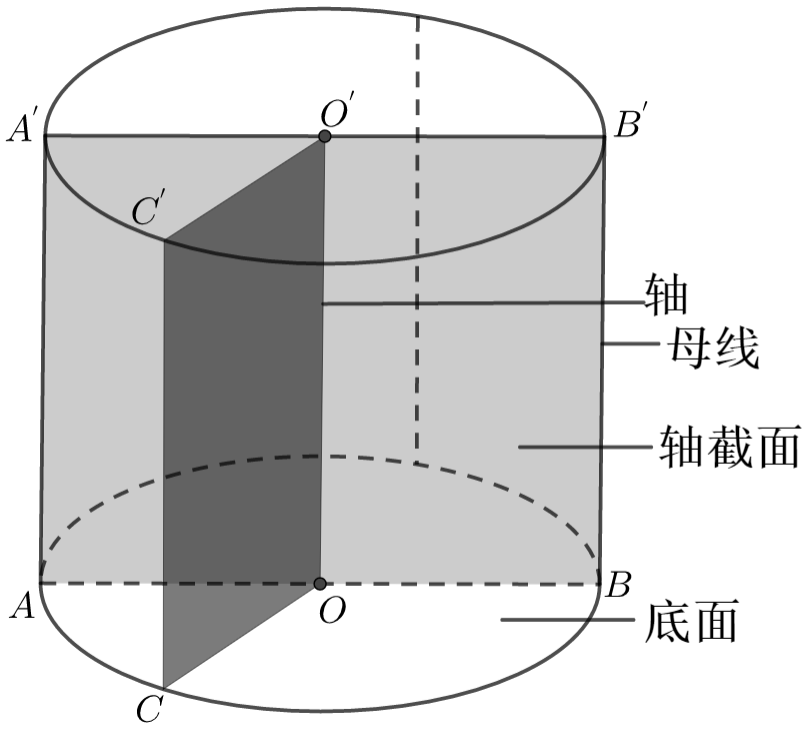
(1)概念
以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱.
(2)性质
上、下底及平行于底面的截面都是等圆;过轴的截面(轴截面)是全等的矩形.
(3)侧面展开图
圆柱的侧面展开图是以底面周长和母线长为邻边的矩形.
6 圆锥
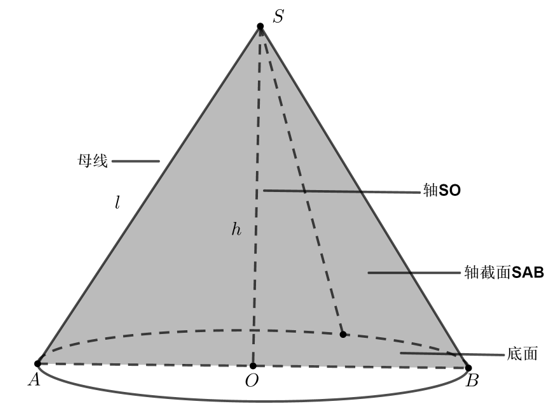
(1)概念
以直角三角形的一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆锥.
(2)性质
平行于底面的截面都是圆,截面直径与底面直径之比等于顶点到截面的距离与顶点到底面的距离之比;
轴截面是等腰三角形;如右图:三角形\(SAB\)
如上图:\(l^{2}=h^{2}+r^{2}\).
(3)侧面展开图
圆锥的侧面展开图是以顶点为圆心,以母线长为半径的扇形.
7圆台
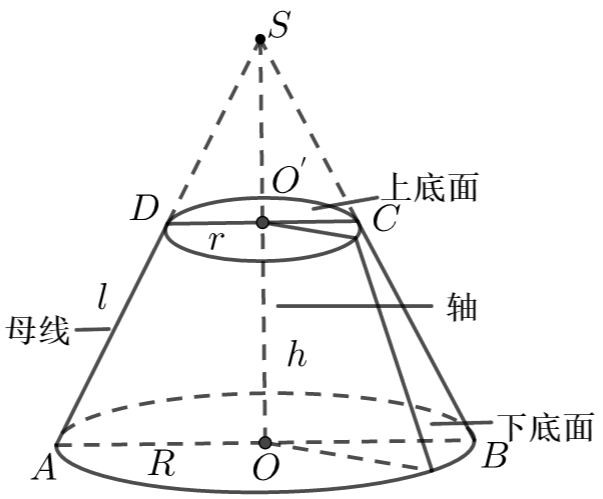
(1)概念
用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台.
8 球体
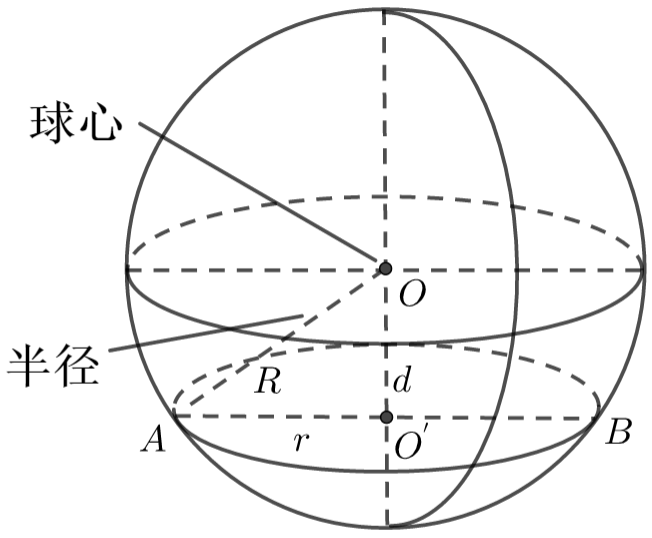
(1)概念
以半圆的直径所在直线为旋转轴,半圆旋转一周形成的旋转体叫做球体,简称球.
(2)性质
① 球心与截面圆心的连线垂直于截面;
② \(R^{2}=r^{2}+d^{2}\)(其中,球心到截面的距离为\(d\)、球的半径为\(R\)、截面的半径为\(r\)).
空间几何体的直观图
1 空间几何体的直观图
用来表示空间几何体的平面图形叫做空间几何体的直观图,常用斜二测画法画它们的直观图.
2 用斜二测画法画水平放置的平面图形的直观图,一般步骤如下:
① 建立平面直角坐标系: 在已知平面图形中取互相垂直的\(x\)轴和\(y\)轴,两轴相交于点\(O\).
② 画出斜坐标系: 在画直观图的纸上(平面上)画出对应的\(x'\)轴和\(y'\)轴, 两轴相交于点\(O'\),且使\(∠x'O'y' =45\)度(或\(135\)度), 它们确定的平面表示水平平面.
③ 画对应图形: 在已知图形平行于\(x\)轴的线段, 在直观图中画成平行于\(x'\)轴, 长度保持不变.在已知图形平行于\(y\)轴的线段, 在直观图中画成平行于\(y'\)轴, 且长度为原来一半.
④ 对于一般线段,要在原来的图形中从线段的各个端点引垂线,再按上述要求画出这些线段,确定端点,从而画出线段.
⑤ 擦去辅助线: 图画好后,要擦去\(x'\)轴,\(y'\)轴及为画图添加的辅助线.
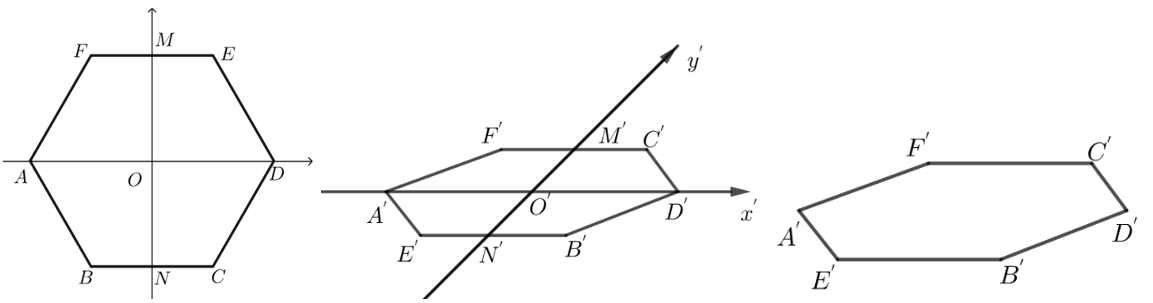
3 斜二测画法口诀
平行依旧垂改斜,横等纵半竖不变,眼见为实遮为虚.
4 斜二侧画法的面积是原来图形面积的\(\dfrac{\sqrt{2}}{4}\)倍.
(原来的高变成了\(45°\)的线段,且长度是原高的一半,因此新图形的高是这个一半线段的\(\dfrac{\sqrt{2}}{2}\)倍,故新高是原来高的\(\dfrac{\sqrt{2}}{4}\),而横向长度不变,所以面积变为原面积的\(\dfrac{\sqrt{2}}{4}\).)
经典例题
【题型一】空间几何体的结构特征
【典题1】 给出下列命题:
① 底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
② 若有两个侧面垂直于底面,则该四棱柱为直四棱柱;
③ 一个棱锥可以有两个侧棱和底面垂直;
④ 一个棱锥可以有两个侧面和底面垂直;
⑤ 所有侧面都是正方形的四棱柱一定是正方体.
其中正确的命题是( )
A. $ (1) (2) $ \(\qquad \qquad \qquad \qquad\)B. $ (1) $ \(\qquad \qquad \qquad \qquad\) C. $ (2) (3) $ \(\qquad \qquad \qquad \qquad\)D. $ (4) $
【解析】 对于①,底面是等边三角形,侧面都是等腰三角形的三棱锥不一定是正三棱锥,如图所示,
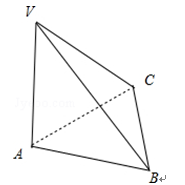
若\(AB=BC=AC=VA\),且\(VA⊥\)平面\(ABC\),但三棱锥\(V-ABC\)表示正三棱锥,\(∴\)①错误;
对于②,当有两个侧面垂直于底面时,该四棱柱不一定为直四棱柱,
如两个侧面不是相邻的时,侧棱与底面不一定垂直,\(∴\)②错误;
对于③,一个棱锥不能有两条侧棱和底面垂直,否则,这两条侧棱互相平行,\(∴\)③错误;
对于④,一个棱锥可以有两个侧面和底面垂直,如①中图形,\(∴\)④正确;
对于⑤,所有侧面都是正方形的四棱柱不一定是正方体,
\(∵\)各相邻侧面并不一定都互相垂直,\(∴\)⑤错误.
综上,正确的命题是④.
故选:\(D\).
【点拨】
① 正三棱锥是底面是等边三角形,三个侧面是全等的等腰三角形的三棱锥.
正四面体是每个面都是全等的等边三角形的三棱锥,正四面体是特殊的正三棱锥;
② 若判断含“一定”“都是”之类绝对性字眼的命题是错误,举一个反例就行,比如判断命题②、⑤;若命题是含“可能”字眼的,便举个正例,比如判断命题④;
③ 判断命题③,利用了反证法.
【典题2】 如图所示,在一个长方体的容器中,里面装有少量水,现在将容器绕着其底部的一条棱倾斜,在倾斜的过程中:
(1)水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)水的形状也不断变化,可能是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底部的一个顶点,水面的形状,水的形状有何变化?

【解析】 (1)不对;水面的形状就是用一个与棱(将长方体倾斜时固定不动的棱)平行的平面截长方体时截面的形状,可以是矩形,但不可能是其他非矩形的平行四边形.易得四边形\(FGHE\)是平行四边形,
又\(∵B_1 C_1⊥\)平面\(CC_1 D_1 D\),
\(GF//B_1 C_1⇒GF⊥\)平面\(CC_1 D_1 D⇒GF⊥HG\)
\(∴\)四边形\(FGHE\)是矩形;
(2)不对;水的形状就是用与棱(将长方体倾斜时固定不动的棱)平行的平面将长方体截去一部分的几何体,此几何体是棱柱,水比较少时,是三棱柱;水多时,可能是四棱柱或五棱柱,但不可能是棱台或棱锥.
(3)用任意一个平面去截长方体,其截面形状可以是三角形、四边形、五边形、六边形,因而水面的形状可以是三角形、四边形、五边形、六边形;水的形状可以是棱锥、棱柱,但不可能是棱台.
【点拨】
本题中水的形状就是用与棱(将长方体倾斜时固定不动的棱)平行的平面将长方体截去一部分的几何体,第一要注意多种情况的考虑,比如可以想象平面\(α\)逐渐往上升,截面会出现多少种情况;第二要有什么量是不变的,主要就是平面\(FGHE\)均与平面\(BB_1 A_1 A\)、平面\(CC_1 D_1 D\)垂直的关系.
巩固练习
1 (★) 给出下列三个命题
①有四个相邻侧面互相垂直的棱柱是直棱柱;
②各侧面都是正方形的四棱柱是正方体;
③底面是正三角形,各侧面都是等腰三角形的三棱锥是正三棱锥.
其中真命题的个数是 ( )
A. \(1\) \(\qquad \qquad \qquad \qquad\) B. \(2\) \(\qquad \qquad \qquad \qquad\)C. $ 3$ \(\qquad \qquad \qquad \qquad\)D. \(0\)
2 (★) 一个棱柱是正四棱柱的条件是( )
A、底面是正方形,有两个侧面是矩形
B、底面是正方形,有两个侧面垂直于底面
C、底面是菱形,且有一个顶点处的三条棱两两垂直
D、每个侧面都是全等矩形的四棱柱
3 (★★) 在一个棱长为的正方体内,你认为最多放入的直径为的球的个数为 ( )
A. \(64\) \(\qquad \qquad \qquad \qquad\) B. \(65\) \(\qquad \qquad \qquad \qquad\)C. \(66\) \(\qquad \qquad \qquad \qquad\)D. \(67\)
4 (★★) 如图是由三根细铁杆\(PA、PB、PC\)组成的支架,三根杆的两两夹角都是\(60°\),一个半径为\(1\)的球放在支架上,则球心\(O\)到点\(P\)的距离为( )

A. \(\sqrt{2}\) \(\qquad \qquad \qquad \qquad\) B. \(\sqrt{3}\) \(\qquad \qquad \qquad \qquad\)C. \(2\) \(\qquad \qquad \qquad \qquad\)D. \(\dfrac{3}{2}\)
参考答案
-
【答案】 \(D\)
【解析】 四个侧面互相垂直的棱柱并不能保证侧棱一定垂直于底面,故①错误;
当底面是菱形时,各侧面也可以是正方形,故②错误;
当锐角为\(60°\)的菱形沿短的对角线折成本棱锥时,有可能不是正三棱锥,
举个特殊的三棱锥底面是正三角形,一个为等腰三角形的侧面与底面垂直,
这时三侧面中,有一个是正三角形,两个是等腰三角形,故③错误.故选 \(D\). -
【答案】 \(D\)
【解析】 上、下底面都是正方形,且侧棱垂直于底面的棱柱叫做正四棱柱.
故\(A\)和\(B\)错在有可能是斜棱柱,
\(C\)错在上下底面有可能不是正方形,
\(D\):底面是菱形,且有一个顶点处的三条棱两两垂直能保证上、下底面都是正方形,且侧棱垂直于底面.
故选\(D\). -
【答案】 \(C\)
【解析】 根据球体的特点,最多应该是放\(5\)层,第一层能放\(16\)个;
第\(2\)层放在每\(4\)个小球中间的空隙,共放\(9\)个;第\(3\)层继续往空隙放,可放\(16\)个;
第\(4\)层同第\(2\)层放\(9\)个;第\(5\)层同第\(1、3\)层能放\(16\)个,
所以最多可以放入小球的个数\(16+9+16+9+16=66\) (个).故选\(C\). -
【答案】 \(B\)
【解析】 连接\(OP\)交平面\(ABC\)于\(O′\),
\(∵\)三根铁杆的两两夹角都是\(60°\),\(∴△ABC\)和\(△PAB\)为正三角形,
\(\therefore O^{\prime} A=\dfrac{\sqrt{3}}{3} A B=\dfrac{\sqrt{3}}{3} P A\),
\(\because A O^{\prime} \perp P O\),\(O A \perp P A\),
\(\therefore \triangle A O^{\prime} P \backsim \triangle O A P\),\(\therefore \dfrac{A O r}{A P}=\dfrac{O A}{O P}\),\(\therefore O P=\sqrt{3} O A\)
\(∵\)半径\(OA=1\),\(\therefore O P=\sqrt{3}\).
故选\(B\).

【题型二】空间几何体的折叠和展开
【典题1】 如图,在长方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(AB=BC=1\),\(A A_{1}=\sqrt{3}\),点\(E\)为棱\(AB\)上的动点,则\(D_1 E+CE\)的最小值为( )
A. \(2 \sqrt{2}\) \(\qquad \qquad \qquad \qquad\) B. \(\sqrt{10}\) \(\qquad \qquad \qquad \qquad\) C. \(2+\sqrt{2}\) \(\qquad \qquad \qquad \qquad\)D. \(\sqrt{5}+1\)

【解析】 画出几何体的图形,连结\(D_1 A\),延长至\(G\),使得\(AG=AD\),连结\(C_1 B\),延长至\(F\),使得\(BF=BC\),连结\(EF\),则\(ABFG\)为正方形,

连结\(D_1 F\),则\(D_1 F\)为\(D_1 E+CE\)的最小值,\(D_{1} F=\sqrt{1+9}=\sqrt{10}\)
\(∴D_1 E+CE\)取最小值 .故选:\(B\).
【点拨】 此题属于“最短路径问题”:要让线段\(D_1 E\)与\(EF\)共面,其实就是把平面\(ABCD\)沿着线段\(AB\)展开到与平面\(D_1 C_1 BA\)共面,则\(D_1 E+CE\)的最小值显然是\(D_1 F\),把立体几何问题转化为平面几何问题.
【典题2】 小红去礼品店给大毛买了一盒生日礼物,礼盒是长、宽、高分别为\(20cm、20cm、5cm\)的长方体.为美观起见,礼品店服务员用彩绳做了一个新颖的捆扎.如图所示,彩绳以\(A\)为起点,现沿着\(AB→BC→CD→DE\)\(→EF→FG→GH→HA\)环绕礼盒进行捆扎,其中分别为下底面各棱的中点,\(C、D、G、H\)分别为上底面各棱上一点,则所用包装彩绳的最短长度为( )

A. $ (40+15 \sqrt{2}) \mathrm{cm}$ \(\qquad \qquad \qquad \qquad\) B. $ (40+30 \sqrt{2}) \mathrm{cm}$
C. $ (40+15 \sqrt{5}) \mathrm{cm}$ \(\qquad \qquad \qquad \qquad\) D. $ (40+30 \sqrt{5}) \mathrm{cm}$
【解析】 由\(A、B、E、F\)分别为下底面各棱的中点,可得\(AB+EF=20+20=40\),由对称性可得要求所用包装彩绳的最短长度,可求\(BC+CD+DE\)的最小值,可将\(BC,CD,DE\)所在的平面展开到一个平面上,如图所示可得\(B,C,D,E\)四点共线时,\(BC+CD+DE\)的和取得最小值\(15 \sqrt{2}\),则所用包装彩绳的最短长度为\(40+30 \sqrt{2} \mathrm{~cm}\).故选\(B\).

巩固练习
1 (★) 下面图形中是正方体展开图的是( )

2 (★★) 如图一个封闭的立方体,它\(6\)个表面各标出\(1、2、3、4、5、6\)这\(6\)个数字,现放成下面\(3\)个不同的位置,则数字\(1、2、3\)对面的数字是 ( )

A.\(4、5、6\) \(\qquad \qquad \qquad\) B.\(6、4、5\) \(\qquad \qquad \qquad\) C.\(5、6、4\) \(\qquad \qquad \qquad\) D.\(5、4、6\)
3 (★★) 北方的冬天户外冰天雪地,若水管裸露在外,则管内的水就会结冰从而冻裂水管,给用户生活带来不便.每年冬天来临前,工作人员就会给裸露在外的水管“保暖” 在水管外面包裹保温带,用一条保温带盘旋而上一次包裹到位.某工作人员采用四层包裹法(除水管两端外包裹水管的保温带都是四层) 如图\(1\)所示是相邻四层保温带的下边缘轮廓线,相邻两条轮廓线的间距是带宽的四分之一.设水管的直径与保温带的宽度都为\(4cm\).在图\(2\)水管的侧面展开图中,此保温带的轮廓线与水管母线所成的角的余弦值是(保温带厚度忽略不计)( )

A. \(\dfrac{1}{4}\) \(\qquad \qquad \qquad \qquad\)B. \(\dfrac{1}{4 \pi}\) \(\qquad \qquad \qquad \qquad\) C. $ \dfrac{\sqrt{1+4 \pi^{2}}}{1+4 \pi^{2}}$ \(\qquad \qquad \qquad \qquad\) D. $ \dfrac{\sqrt{1+16 \pi^{2}}}{1+16 \pi^{2}}$
4 (★★) 如图,把边长为\(a\)的正方形剪去图中的阴影部分,沿图中所画的折成一个正三棱锥,则这个正三棱锥的高是( )

A. \(\dfrac{1}{3} \sqrt{3+2 \sqrt{3}} a\) \(\qquad \qquad\)B. $ \dfrac{1}{3} \sqrt{3-\sqrt{3}} a$ \(\qquad \qquad\) C. \(\dfrac{1}{3} \sqrt{2+\sqrt{3}} a\) \(\qquad \qquad\)D. \(\dfrac{1}{3} \sqrt{3+3 \sqrt{3}} a\)
5 (★★★) 如图所示,在正三棱柱\(ABC-A_1 B_1 C_1\)中,\(AB=2\),\(AA_1=2\),由顶点\(B\)沿棱柱侧面(经过棱\(AA_1\))到达顶点\(C_1\),与\(AA_1\)的交点记为\(M\).求:

(1)三棱柱侧面展开图的对角线长;
(2)从\(B\)经\(M\)到\(C_1\)的最短路线长及此时\(\dfrac{A_{1} M}{A M}\)的值.

参考答案
- 【答案】 \(A\)
【解析】 由正方体表面展开图性质知\(A\)是正方体的展开图;
\(B\)折叠后第一行两个面无法折起来,而且下边没有面,故不能折成正方体;
\(C\)缺少一个正方形;\(B\)折叠后有一个面重合,另外还少一个面,故不成正方体.故选\(A\). - 【答案】 \(D\)
【解析】 第一个正方体已知\(1,2,3\)第二个正方体已知\(1,3,4\)第三个正方体已知\(2,3,5\)且不同的面上写的数字各不相同,则可知\(1\)对面标的是\(5\),\(2\)对面标的是\(4\),\(3\)对面标的是\(6\),故选\(D\). - 【答案】 \(D\)
【解析】 过点\(A\)作\(AE⊥D′B′\),垂足为\(E\),
其展开图如图所示

由水管直径为\(4cm\),所以水管的周长为\(AE=4πcm\),
则\(∠AB'E=α\),
又\(B E=\dfrac{1}{4} \times 4=1\),\(A B^{\prime}=\sqrt{1^{2}+(4 \pi)^{2}}=\sqrt{1+16 \pi^{2}}\)
所以\(\cos \angle \alpha=\dfrac{B^{\prime} E}{A B^{\prime}}=\dfrac{1}{\sqrt{1+16 \pi^{2}}}=\dfrac{\sqrt{1+16 \pi^{2}}}{1+16 \pi^{2}}\).
故选\(D\). - 【答案】 \(D\)
【解析】 折叠之后的正三棱锥如图,其中\(PA=PB=PC=a\),
\(A B=A C=B C=b\),\(A O=\dfrac{2}{3} A D=\dfrac{2}{3} \cdot \dfrac{\sqrt{3}}{2} b=\dfrac{\sqrt{3}}{3} b\),
\(\therefore P O=\sqrt{P A^{2}-A O^{2}}=\sqrt{a^{2}-\dfrac{1}{3} b^{2}}\),①
\(\because \angle P A C=30^{\circ}\),
\(\therefore A C^{2}=P A^{2}+P C^{2}-2 P A \cdot P C \cdot \cos 30^{\circ}\),
即\(b^{2}=2 a^{2}-\sqrt{3} a^{2}=(2-\sqrt{3}) a^{2}\),
代入①,得\(P O=\sqrt{\dfrac{1+\sqrt{3}}{3}} a=\dfrac{1}{3} \sqrt{3+3 \sqrt{3}} a\).
故选 \(D\). - 【答案】 \((1) 2 \sqrt{10} (2) 1\)
【解析】 沿侧棱\(B B_{1}\)将正三棱柱的侧面展开,得到一个矩形\(B B_{1} B_{1}^{\prime} B^{\prime}\).
(1)矩形\(B B_{1} B_{1}^{\prime} B^{\prime}\)的长\(B B^{\prime}=6\),宽\(B B_{1}=2\).
所以三棱柱侧面展开图的对角线长为\(\sqrt{6^{2}+2^{2}}=2 \sqrt{10}\).
(2)由侧面展开图可知:当\(B,M,C_1\)三点共线时,由\(B\)经\(M\)到点\(C_1\)的路线最短.
所以最短路线长为\(B C_{1}=\sqrt{4^{2}+2^{2}}=2 \sqrt{5}\).
显然\(R t \triangle A B M \cong R t \triangle A_{1} C_{1} M\),
所以\(A_1 M=AM\),即\(\dfrac{A_{1} M}{A M}=1\).
【题型三】 斜二测画法
【典题1】 如图,\(\triangle A^{\prime} B^{\prime} C^{\prime}\)是\(△ABC\)的直观图,其中\(A'B'=A'C'\),\(A'B'∥x'\)轴,\(A'C'∥y'\)轴,那么\(△ABC\)是( )

A.等腰三角形 \(\qquad \qquad \qquad\)B.钝角三角形\(\qquad \qquad \qquad\) C.等腰直角三角形\(\qquad \qquad \qquad\) D.直角三角形
【解析】 根据斜二测画法中平行与坐标轴的直线,平行关系不变,且平行于\(x\)轴的线段,长度不变,平行于\(y\)轴的线段,长度变为原来的一半,
\(∴\)直观图\(\triangle A^{\prime} B^{\prime} C^{\prime}\)的原来图形\(△ABC\)是直角三角形,且\(AC=2AB\),不是等腰直角三角形.
故选:\(D\).
【点拨】 斜二测法:平行于\(x\)轴的线段,长度不变,平行于\(y\)轴的线段,长度变为原来的一半.
【典题2】 梯形\(A_1 B_1 C_1 D_1\)(如图)是一水平放置的平面图形\(ABCD\)的直观图(斜二测),若\(A_1 D_1∥y'\)轴,\(A_1 B_1∥x'\)轴,\(A_{1} B_{1}=\dfrac{2}{3} C_{1} D_{1}=2\),\(A_1 D_1=1\),则平面图形\(ABCD\)的面积是( )

A. \(5\) \(\qquad \qquad \qquad \qquad\)B. \(10\) \(\qquad \qquad \qquad \qquad\) C. \(5 \sqrt{2}\) \(\qquad \qquad \qquad \qquad\)D. \(10 \sqrt{2}\)
【解析】 方法一 如图,根据直观图画法的规则,
直观图中\(A_1 D_1∥O'y'\),\(A_1 D_1=1\),\(⇒\)原图中\(AD∥Oy\),
从而得出\(AD⊥DC\),且\(AD=2A_1 D_1=2\),
直观图中\(A_1 B_1∥C_1 D_1\),\(A_{1} B_{1}=\dfrac{2}{3} C_{1} D_{1}=2\),
⇒原图中\(AB∥CD\),\(A B=\dfrac{2}{3} C D=2\),
即四边形\(ABCD\)上底和下底边长分别为\(2\),\(3\),高为\(2\),如图.
故其面积\(S=\dfrac{1}{2}(2+3) \times 2=5\);
故选:\(A\).

方法二 \(∵∠A_1 D_1 O_1=45^°\),\(∴\)梯形的高\(h=A_{1} D_{1} \cos 45^{\circ}=\dfrac{\sqrt{2}}{2}\)
\(\therefore S_{\text {梯形 } A_{1} B_{1} C_{1} D_{1}}=\dfrac{5 \sqrt{2}}{4}\)
\(∴\)平面图形\(ABCD\)的面积是\(\dfrac{5 \sqrt{2}}{4} \times 2 \sqrt{2}=5\).
【点拨】 斜二侧画法的面积是原来图形面积的\(\dfrac{\sqrt{2}}{4}\)倍,原来图形的面积是斜二侧画法的面积的\(2 \sqrt{2}\)倍.
巩固练习
1 (★) 如图所示的是水平放置的三角形直观图,\(D'\)是\(\triangle A^{\prime} B^{\prime} C^{\prime}\)中\(B'C'\)边上的一点,且\(D'\)离\(B'\)比\(D'\)离\(C'\)近,又\(A'D'∥y'\)轴,那么原\(△ABC\)的\(AB\)、\(AD\)、\(AC\)三条线段中( )

A.最长的是\(AB\),最短的是\(AC\) \(\qquad \qquad \qquad \qquad\)B.最长的是\(AC\),最短的是\(AD\)
C.最长的是\(AD\),最短的是\(AC\) \(\qquad \qquad \qquad \qquad\)D.最长的是\(AB\),最短的是\(AD\)
2 (★) 利用斜二测画法画出\(△ABO\)的直观图(如图),已知\(O'B'=2\),\(A'B'∥y'\)轴,过\(A'\)作\(A'C'⊥x\)轴于\(C'\),若\(△ABO\)的面积为\(4\),则\(A'C'\)的长为( )

A. \(8 \sqrt{2}\) \(\qquad \qquad \qquad \qquad\) B. \(4 \sqrt{2}\) \(\qquad \qquad \qquad \qquad\)C. \(2 \sqrt{2}\) \(\qquad \qquad \qquad \qquad\)D. \(\sqrt{2}\)
3 (★) 正三角形\(ABC\)的边长为\(2cm\),如图,\(\triangle A^{\prime} B^{\prime} C^{\prime}\)为其水平放置的直观图,则\(\triangle A^{\prime} B^{\prime} C^{\prime}\)的周长为( )

A. \(8 \mathrm{~cm}\) \(\qquad \qquad \qquad\) B. \(6 \mathrm{~cm}\) \(\qquad \qquad \qquad\) C. $ (2+\sqrt{6}) \mathrm{cm}$ \(\qquad \qquad \qquad\)D. $ (2+2 \sqrt{3}) \mathrm{cm}$
参考答案
- 【答案】 \(B\)
【解析】 由题意得到原\(△ABC\)的平面图为:
其中,\(AD⊥BC\),\(BD<DC\),所以\(AC>AB>AD\),
所以\(△ABC\)的\(AB、AC、AD\)三条线段中最长的是\(AC\),最短的是\(AD\).
故选:\(B\).

- 【答案】 \(D\)
【解析】 根据斜二测画法知,\(O^{\prime} B^{\prime}=2\),\(∴OB=2\),
又\(△ABO\)的面积为\(S_{\triangle A B O}=\dfrac{1}{2} \times 2 \times 2 B^{\prime} A^{\prime}=4\),
\(∴B′A′=2\),
\(\therefore A^{\prime} C^{\prime}=B^{\prime} A^{\prime} \sin 45^{\circ}=2 \times \dfrac{\sqrt{2}}{2}=\sqrt{2}\).
故选:\(D\). - 【答案】 \(C\)
【解析】 正\(△ABC\)的边长为\(2cm,\),
则它的直观图\(\triangle A^{\prime} B^{\prime} C^{\prime}\)中,\(A^{\prime} B^{\prime}=2\),\(O^{\prime} C^{\prime}=\dfrac{1}{2} \cdot 2 \cdot \sin 60^{\circ}=\dfrac{\sqrt{3}}{2}\);
\(\therefore B^{\prime} C^{\prime 2}=O^{\prime} B^{\prime 2}+O^{\prime} C^{\prime 2}-2 O^{\prime} B^{\prime} \cdot O^{\prime} C^{\prime} \cdot \cos 45^{\circ}\) \(=1+\dfrac{3}{4}-2 \times 1 \times \dfrac{\sqrt{3}}{2} \times \dfrac{\sqrt{2}}{2}=\dfrac{7-2 \sqrt{6}}{4}=\left(\dfrac{\sqrt{6}-1}{2}\right)^{2}\) ,
\(\therefore B^{\prime} C^{\prime}=\dfrac{\sqrt{6}-1}{2}\);
又\(A^{\prime} C^{\prime 2}=O^{\prime} A^{\prime 2}+O^{\prime} C^{\prime 2}-2 O^{\prime} A^{\prime} \cdot O^{\prime} C^{\prime} \cdot \cos 135^{\circ}\)
\(=1+\dfrac{3}{4}-2 \times 1 \times \dfrac{\sqrt{3}}{2} \times\left(-\dfrac{\sqrt{2}}{2}\right)\)\(=\dfrac{7+2 \sqrt{6}}{4}=\left(\dfrac{\sqrt{6}+1}{2}\right)^{2}\)
\(\therefore A^{\prime} C^{\prime}=\dfrac{\sqrt{6}+1}{2}\);
\(\therefore \triangle A^{\prime} B^{\prime} C^{\prime}\)的周长为\(2+\dfrac{\sqrt{6}-1}{2}+\dfrac{\sqrt{6}+1}{2}=(2+\sqrt{6})(\mathrm{cm})\).
故选:\(C\).


