8.4 平面与空间点、直线、面之间的位置关系

\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】高一数学下学期同步知识点剖析精品讲义！
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}\)

必修第二册同步拔高，难度3颗星！

模块导图

知识剖析

平面

无限延展，无边界.
判断一张纸是一个平面(×)；
平面\(ABCD\)就是四边形\(ABCD\) (×)；
两个平面可相交于一点 (×).
原因均是平面是无限延展的.

三个基本事实与三个推论

1 基本事实1
不共线的三点确定一个平面.

注 “确定”的意思是“有且只有”，过不共线三点的平面有且只有一个，故说确定一个平面.
判断三点确定一个平面 (×)；原因是三点未必共线.
用途:用于确定平面.

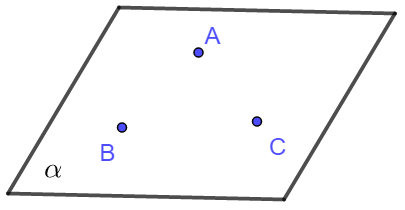
2 基本事实2
如果一条直线上有两点在一个平面内，那么直线在平面内.
用途:常用于证明直线在平面内.

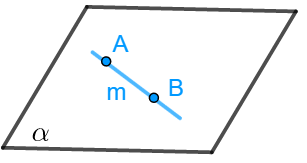
3 基本事实3
如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.
用途:常用于证明线在面内，证明点在线上.

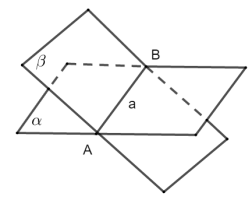
推论1:直线与直线外的一点确定一个平面.
推论2:两条相交直线确定一个平面.
推论3:两条平行直线确定一个平面.

图形语言，文字语言，符号语言的转化

图形语言	文字语言	符号语言
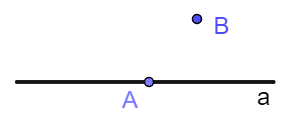	点\(A\)在直线\(a\)上，点\(B\)在直线\(a\)外	\(A \in a，B \notin a\)
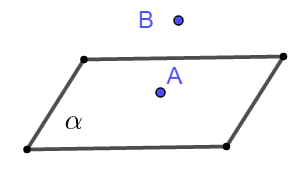	点\(A\)在平面\(\alpha\)内，点\(B\)在平面\(\alpha\)外	\(A \subset \alpha，B \nsubseteq \alpha\)
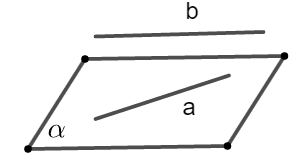	直线\(a\)在平面\(\alpha\)内，直线\(b\)在平面\(\alpha\)外	\(a \subset \alpha，b \nsubseteq \alpha\)
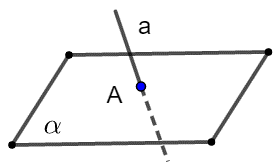	直线\(a\)与平面\(\alpha\)相交于点	\(a \cap \alpha=A\)
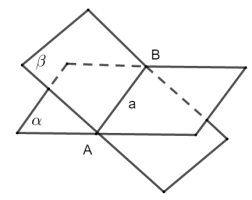	平面\(\alpha\)与平面\(\beta\)相交于直线\(a\)	\(\alpha \cap \beta=a\)

注点用大写字母表示，直线用小写字母表示，平面用希腊字母表示.

空间点，直线，面之间的位置关系

1 线线的位置关系
(1) 空间直线的位置关系

\[\left\{\begin{array}{l} \text { 共面: } a \cap b=A， a / / b \\ \text { 异面: } a \text { 与 } b \text { 异面 } \end{array}\right.\]

(2) 平行线的传递公理
平行于同一条直线的两条直线互相平行.
符号表述:\(a // b\)，\(b / / c⟹ a / / c\)

(3) 等角定理
如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补.

(4) 异面直线
(i) 定义：不同在任何一个平面内的两条直线——异面直线；
(ii) 图形语言

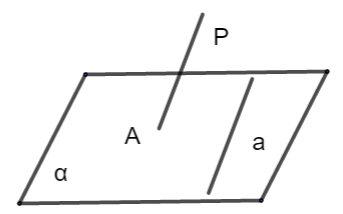
符号语言

\[\left.\begin{array}{l} P \notin \alpha \\ A \in \alpha \\ a \in \alpha \\ A \notin \alpha \end{array}\right\} \Rightarrow P A \text { 与 } a \text { 异面 }\]

2 线面的位置关系
(1) 直线与平面的位置关系

\[\left\{\begin{array}{l} l \subset \alpha \quad \text { 在面内 } \\ l \cap \alpha=A \text { 相交 } \\ l / / \alpha \quad \text { 平行 } \end{array}\right.\]

(2) 图形语言

例若直线\(a\)在平面\(M\)内，直线\(m\)平行直线\(a\)，则直线\(m\)与平面\(M\)的位置关系是 \(\underline{\quad \quad}\) .
答案 \(m//M\)或者\(m⊂M\).

3 面面的位置关系
(1) 平面与平面的位置关系

\[\begin{cases}\alpha / / \beta & \text { 平行 } \\ \alpha \cap \beta= a &\text { 斜交 } \\ \alpha \perp \beta & \text { 垂直 }\end{cases} \]

(2) 图形语言

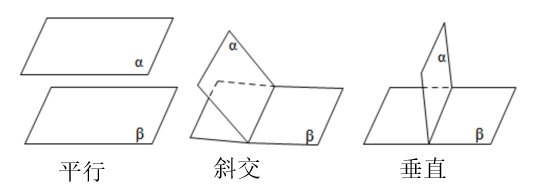
经典例题

【题型一】平面的确定

【典题1】 设\(P\)表示一个点，\(a\) ，\(b\)表示两条直线，\(α\) ，\(β\)表示两个平面，给出下列四个命题，其中正确的命题是 (　　)．
① \(P∈a ，P∈α⇒a⊂α\)
② \(a∩b=P ，b⊂β⇒a⊂β\)　
③ \(a∥b ，a⊂α ，P∈b ，P∈α⇒b⊂α\)
④ \(α∩β=b ，P∈α ，P∈β⇒P∈b\)
A. \((1) (2)\) \(\qquad \qquad \qquad \qquad\) B. \((2) (3)\) \(\qquad \qquad \qquad \qquad\)C. \((1) (4)\) \(\qquad \qquad \qquad \qquad\) D. \((3) (4)\)
【解析】 对于① 当\(a∩α=P\)时，\(P∈a\)，\(P∈α\)，但\(a⊄α\)，①错；
对于②\(a∩β=P\)时，②错；
对于③ 如图，\(∵a //b\) ，\(P∈b\) ，\(∴P∉a\) ，\(∴\)由直线\(a\)与点\(P\)确定唯一平面\(α\)，

又\(a∥b\)，由\(a\)与\(b\)确定唯一平面\(β\)，但\(β\)经过直线\(a\)与点\(P\) ，\(∴β\)与\(α\)重合，\(∴b⊂α\) ，故③正确；
对于④ \(P∈α\)，\(P∈β⇒\)点\(P\)是平面\(α、β\)的公共点，\(α∩β=b⇒\)线\(b\)是平面\(α、β\)的交线，而两平面的交点必在其交线上，故④正确．故选\(D\).
【点拨】
① 熟悉点、线、面及其之间关系的符号表示；
② 判断尽量利用画图进行思考，若要排除选项则举出一反例；
③ 确定平面的方法---不共线的三点确定一个平面、直线与直线外的一点确定一个平面、两条相交直线确定一个平面、两条平行直线确定一个平面.

【典题2】 在正方体\(ABCD—A_1 B_1 C_1 D_1\)中，\(E\)，\(F\)分别为棱\(AA_1\)，\(CC_1\)的中点，则在空间中与三条直线\(A_1 D_1\)，\(EF\)，\(CD\)都相交的直线有\(\underline{\quad \quad}\)条．
【解析】 在\(EF\)上任意取一点\(M\)，直线\(A_1 D_1\)与\(M\)确定一个平面，这个平面与\(CD\)有且仅有\(1\)个交点\(N\)，当\(M\)取不同的位置时就确定不同的平面，从而与\(CD\)有不同的交点\(N\)，而直线\(MN\)与这\(3\)条异面直线都有交点如图所示．

【点拨】
其实就是过三直线\(A_1 D_1\)，\(EF\)，\(CD\)中任一条直线的平面与另外两直线分别交于点\(M、N\)，则直线\(MN\)为所求直线，而这样的平面有无数个，则直线\(MN\)有无数条.

【题型二】三点共线、三线共点、四点共面

【典题1】 如图，在正方体\(ABCD—A_1 B_1 C_1 D_1\)中，点\(P\) ，\(Q\) ，\(R\) 分别在棱\(AB\) ，\(BB_1\) ，\(CC_1\)上，且\(DP\)，\(QR\) 相交于点\(O\)，求证\(O\) ，\(B\) ，\(C\)三点共线.

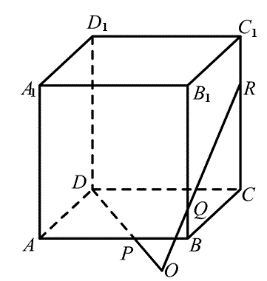
【证明】 \(∵ P\in\)直线\(AB\) ，\(D\in\)直线\(CD\)，
\(\therefore P \in\)平面\(ABCD\) ， \(D \in\)平面\(ABCD\).
\(∴\)直线\(D P \subset\)平面\(ABCD\).
又\(\because O \in\)直线\(DP\)，\(\therefore O \in\)平面\(ABCD\).
同理可证，\(O \in\)平面\(BCC_1 B_1\).
\(∵\)平面\(A B C D \cap\)平面\(BCC_1 B_1=\)直线\(BC\)，
\(\therefore O \in\)直线\(BC\).
\(∴O ，B ，C\) 三点共线.
【点拨】
① 本题利用了基本事实3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.
② 证明三点\(A、B、C\)共线，一般思路是证明点\(A\)在直线\(BC\)上.

【典题2】 如图所示，正方体\(ABCD—A_1 B_1 C_1 D_1\)中，\(E、F\)分别是\(AB\)和\(AA_1\)的中点．
求证:\((1) E、C、D_1 、F\)四点共面；\(\qquad \qquad\)\((2) CE、D_1 F、DA\)三线共点．

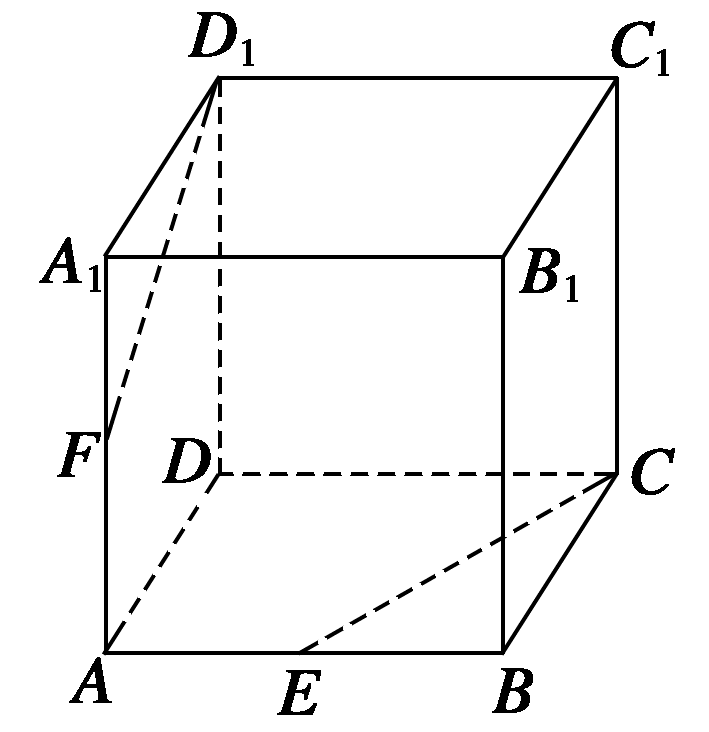
【证明】 　
(1) 连接\(EF\)，\(CD_1\)，\(A_1 B\).
\(∵E、F\)分别是\(AB\)、\(AA_1\)的中点，\(\therefore E F / / A_{1} B\).
又\(A_1 B//D_1 C\) ，\(∴EF//CD_1\)，
\(∴\)直线\(EF\)与直线\(CD_1\)共面，
即\(E、C、D_1 、F\)四点共面．
(2) \(∵EF//CD_1\) ，\(EF<CD_1\) ，
\(∴CE\)与\(D_1 F\)必相交，设交点为\(P\)，
则由\(P \in C E\)，\(C E \subset\)平面\(ABCD\)，得\(P \in\)平面\(ABCD\).
同理\(P \in\)平面\(ADD_1 A_1\).
又平面\(A B C D \cap\)平面\(ADD_1 A_1=DA\)，
\(∴P \in\)直线\(DA\)
\(∴CE、D_1 F、DA\)三线共点．

【点拨】
① 证明四点共面可转化为两线共面，即证明两直线必定相交或平行(利用推论2：两相交线确定一个平面和推论3：两条平行直线确定一个平面)；
② 证明三线\(a，b，c\)共点\(P\)，一般思路是
(1) 先设两直线\(a，b\)相交于点\(P\)，再证明点\(P \in c\).
(2) 证明\(a\)与\(b\)相交于点\(P\)，\(c\)与\(b\)相交于点\(M\)，再证明两交点\(P、M\)重合；
③ 证明多线共面，首先由其中两直线确定平面，再证其余直线在此平面内.

巩固练习

1 (★★) 一块蛋糕切三道最多可以切\(\underline{\quad \quad}\) 块？

2 (★) 下列命题正确的是 (　　)
Ａ.经过三点确定一个平面
Ｂ.经过一条直线和一个点确定一个平面
Ｃ.四边形确定一个平面
Ｄ.两两相交且不共点的三条直线确定一个平面

3 (★) 以下四个命题中，正确命题的个数是 (　　)
①不共面的四点中，其中任意三点不共线；
②若点\(A、B、C、D\)共面，点\(A、B、C、E\)共面，则\(A、B、C、D、E\)共面；
③若直线\(a、b\)共面，直线\(a、c\)共面，则直线\(b、c\)共面；
④依次首尾相接的四条线段必共面．
A. \(0\)　　\(\qquad \qquad \qquad \qquad\) B. \(1\) 　 \(\qquad \qquad \qquad \qquad\) C. \(2\)　　\(\qquad \qquad \qquad \qquad\) 　 D. \(3\)

4 (★★) 空间四边形\(ABCD\)中，各边长均为\(1\)，若\(BD=1\)，则\(AC\)的取值范围是\(\underline{\quad \quad}\)．　

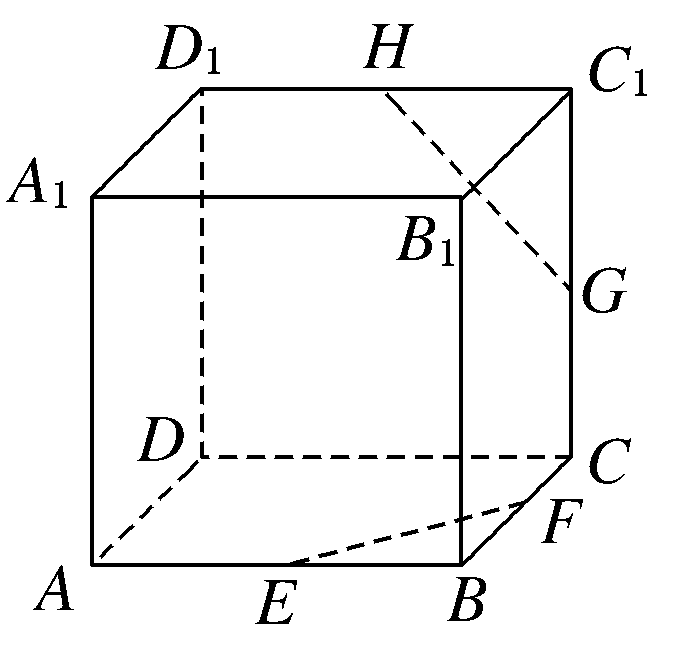
5 (★★★) 如图，已知\(E、F、G、H\)分别是正方体\(ABCD—A_1 B_1 C_1 D_1\)的棱\(AB\)、\(BC\)、\(CC_1\)、\(C_1 D_1\)的中点，证明\(FE、HG、DC\)三线共点．

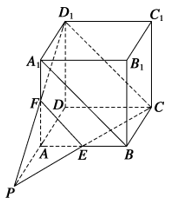
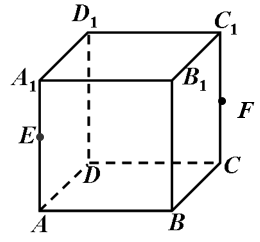
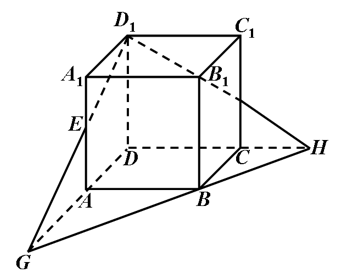
6 (★★★) 如图，在正方体\(ABCD—A_1 B_1 C_1 D_1\)中，点\(E，F\)分别是棱\(AA_1\)，\(CC_1\)的中点，求证点\(D_1，E，F，B\)共面.

参考答案

【答案】 \(8\)
【答案】 \(D\)
【解析】 对于\(A\)，若三点共线时就错了；对于\(B\)，若点在直线上，是不能确定一个平面的；对于\(C\)，空间四边形就不属于平面图形，注意四边形在立体几何里分为平面四边形和空间四边形了。
【答案】 \(B\)
【解析】 ①假设其中有三点共线，则该直线和直线外的另一点确定一个平面．这与四点不共面矛盾，故其中任意三点不共线，所以①正确．②从条件看出两平面有三个公共点\(A、B、C\)，但是若\(A、B、C\)共线，则结论不正确；③不正确；④不正确，因为此时所得的四边形的四条边可以不在一个平面上，如空间四边形．
【答案】 \((0， \sqrt{3})\)
【解析】 如图所示，\(△ABD\)与\(△BCD\)均为边长为\(1\)的正三角形，当\(△ABD\)与\(△CBD\)重合时，\(AC=0\)，将\(△ABD\)以\(BD\)为轴转动，到\(A，B，C，D\)四点再共面时，\(A C=\sqrt{3}\)，故\(AC\)的取值范围是\(0<A C<\sqrt{3}\).
【证明】

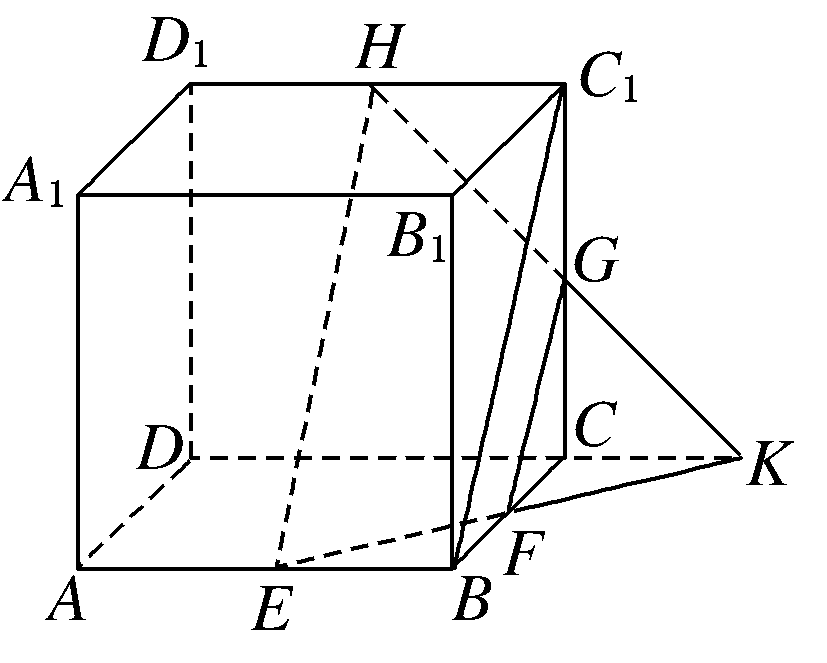
连结\(C_1 B\)，\(HE\)，\(FG\)，由题意知\(HC_1//EB，\) \(HC_1=EB\)，
\(∴\)四边形\(HC_1 BE\)是平行四边形．\(∴HE∥C_1 B\).
又\(C_1 G=GC=CF=BF\)，故\(G F=\dfrac{1}{2} C_{1} B\)，\(GF//C_1 B\)
\(∴GF∥HE\)，且\(GF≠HE\)，\(∴HG\)与\(EF\)相交．
设交点为\(K\)，则\(K \in H G\)，\(H G \subset\)平面\(D_1 C_1 CD\)，
\(\therefore K \in\)平面\(D_1 C_1 CD\).
\(\because K \in E F\)，\(E F \subset\)平面\(ABCD\)，\(∴K∈\)平面\(ABCD\).
\(∵\)平面\(D_1 C_1 CD∩\)平面\(ABCD=DC\)，
\(∴K∈DC\)，\(∴FE、HG、DC\)三线共点．
【证明】
连接\(D_1 E\)，\(D_1 F\)，并分别延长，使\(D_1 F\)与\(DC\)的延长线交于点\(H\)，
\(D_1 E\)的延长线与\(DA\)的延长线交于点\(G\).

\(∵ D_1，E，F\)三点不共线，
\(∴ D_1，E，F\)确定一个平面\(α\)，\(∴ G，H∈α\).
又\(∵\)点\(E\)是\(AA_1\)的中点，
\(\therefore E A / / D D_{1}\)，\(E A=\dfrac{1}{2} D D_{1}\)
\(∴\)点\(A\)是\(DG\)的中点.
同理可得，点\(C\)是\(DH\)的中点.
\(∴ CH = BC = BA = GA\).
又\(∵\) 四边形 \(ABCD\)是正方形，\(∴ ∠BCH = ∠BAG = 90^°\).
连接\(BH\)，\(BG\).
\(∴ △BCH\)，\(△GAB\)是全等的等腰直角三角形.
\(∴ ∠CBH =∠ABG = 45°\).
\(∴ ∠GBA +∠ABC+∠CBH = 180°\).
\(∴ G，B，H\)三点共线.
又\(G，H∈α\)，\(\therefore G H \subset \alpha\)，而\(B∈GH\)， \(∴ B∈α\).
\(∴ D_1，E，F，B\)四点共面.

【题型三】点、线、面的位置关系

【典题1】 分别和两条异面直线都相交的两条直线一定是 (　　)
Ａ.异面直线 \(\qquad \qquad\) Ｂ.相交直线 \(\qquad \qquad\) Ｃ.不相交直线 \(\qquad \qquad\) Ｄ.不平行直线
【解析】 已知直线\(a\)与\(b\)是异面直线，直线\(AB\)与直线\(CD\)分别与两条直线\(a\)与直线\(b\)相交与点\(A ，B，C ，D\)，

根据题意可得当点\(D\)与点\(B\)重合时，两条直线相交，当点\(D\)与点\(B\)不重合时，两条直线异面．
下面证明两条直线不平行
假设直线\(AB\)与直线\(CD\)平行，则\(A ，B ，C ，D\)四点共面，
所以直线\(BD\)与直线\(AC\)共面，
这与直线\(a\)、直线\(b\)异面相互矛盾，
所以假设错误，即直线\(AB\)与直线\(CD\)不平行．
所以分别与两条异面直线都相交的两条直线一定不平行．
故选\(D\)．
【点拨】 证明两条直线不平行时，利用了反证法.

【典题2】 若直线l不平行于平面\(\alpha\)，且\(l \not \subset a\)，则 (　　)
A.\(\alpha\)内所有直线与\(l\)异面
B.\(\alpha\)内不存在与\(l\)平行的直线
C.\(\alpha\)内存在唯一的直线与\(l\)平行
D.\(\alpha\)内的直线与\(l\)都相交
【解析】 若直线\(l\)不平行于平面\(\alpha\)，且\(l⊄a\)，则\(l\)与平面\(\alpha\)相交，
\(\alpha\)内与\(l\)相交的直线在同一面内，故\(A\)选项错误．
直线\(A\)与面相交的点，过此点的所有直线均与\(A\)相交，平面内其他的线则不与其相交，故\(C，D\)项说法错误．
若\(\alpha\)内存在与\(l\)平行的直线，则根据线面平行的判定定理可知\(l\)与面\(\alpha\)平行，已知直线\(l\)不平行于平面\(\alpha\)，故\(\alpha\)内不存在与\(l\)平行的直线，\(B\)项说法正确．
故选\(B\)．
【点拨】
① 线面的位置关系有：在面内\(l⊂α\)，相交\(l∩α=A\)，平行\(l//α\);
② 在证明选项\(B\)的时候利用了反证法.

【典题3】 如果三个平面将空间分成\(6\)个互不重叠的部分，则这三个平面的位置是 (　　)
A．两两相交于三条交线
B．两个平面互相平行，另一平面与它们相交
C．两两相交于同一条直线
D．\(B\)中情况或\(C\)中情况都可能发生
【解析】 \(A\)选项中，若三个平面两两相交，且有三条交线，则把空间分成\(7\)或\(8\)部分；故\(A\)不正确．
\(B\)选项中，若两个平面互相平行，另一平面与它们相交，则把空间分成\(6\)部分；故\(B\)正确．
\(C\)选项中，若三个平面两两相交于同一条直线，则把空间分成\(6\)部分；故\(C\)正确．故选\(D\)．
【点拨】 本题考核空间想象能力，要注意多种情况，可根据交线的条数进行分类讨论.

巩固练习

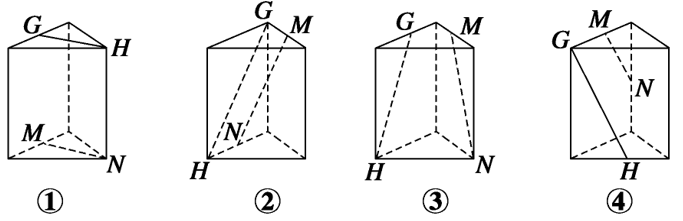
1 (★) 在图中，\(G、H、M、N\)分别是正三棱柱的顶点或所在棱的中点，则表示直线\(GH、MN\)是异面直线的图形有\(\underline{\quad \quad}\)．(填上所有正确答案的序号)

2 (★) 已知直线\(m ，n ，l\)，若\(m∥n\) ，\(n∩l=P\)，则\(m\)与\(l\)的位置关系是 (　　)
A．异面直线 \(\qquad \qquad\) B．相交直线 \(\qquad \qquad\) C．平行直线 \(\qquad \qquad\) D．相交直线或异面直线

3 (★) 下列命题中正确的个数是 ( )
①若直线\(l\)上有无数个点不在平面\(\alpha\)内，则\(l∥ \alpha\).
②若直线\(l\)与平面\(\alpha\)平行，则\(l\)与平面a内的任意一条直线都平行.
③如果两条平行直线中的一条与一个平面平行，那么另一条也与这个平面平行.
④若直线\(l\)与平面\(\alpha\)平行，则\(l\)与平面\(\alpha\)内的任意一条直线都没有公共点.
A．\(0\) \(\qquad \qquad \qquad \qquad\) B．\(1\) \(\qquad \qquad \qquad \qquad\) C．\(2\) \(\qquad \qquad \qquad \qquad\) D．\(3\)

4 (★) 平面\(\alpha\)与平面\(\beta， \gamma\)都相交，则这三个平面可能有（　　）
A．\(1\)条或\(2\)条交线 \(\qquad \qquad \qquad \qquad\) B．\(2\)条或\(3\)条交线
C．仅\(2\)条交线 \(\qquad \qquad \qquad \qquad\) D．\(1\)条或\(2\)条或\(3\)条交线

5 (★) 若三个平面两两相交，则它们的交线条数是 (　　)
A．\(1\)条 \(\qquad \qquad \qquad \qquad\) B．\(2\)条 \(\qquad \qquad \qquad \qquad\) C．\(3\)条 \(\qquad \qquad \qquad \qquad\) D．\(1\)条或\(3\)条

参考答案

【答案】 ② ④
【解析】 　图①中，直线\(GH∥MN\)；
图②中，\(G、H、N\)三点共面，但\(M \notin\)面\(GHN\)，因此直线\(GH\)与\(MN\)异面；
图③中，连接\(MG\)，\(GM∥HN\)，因此\(GH\)与\(MN\)共面；
图④中，\(G、M、N\)共面，但\(H \notin\)面\(GMN\)，因此\(GH\)与\(MN\)异面．
所以图②、④中\(GH\)与\(MN\)异面．
【答案】 \(D\)
【解析】 如图，\(AB∥CD\)，\(CD∩DD_1=D\)，\(∴AB\)与\(DD_1\)异面，\(AB∥CD\)，\(CD∩AD=D\)，\(∴AB\)与\(AD\)相交，
\(∴\)若\(m∥n\)，\(n∩l=P\)，则\(l\)与\(m\)的位置关系相交或异面．故选\(D\)．
【答案】 \(B\)
【解析】 \(B\)，只有④对．
【答案】 \(D\)
【解析】 ①若平面\(β∥\)平面\(γ\)，平面\(α\)与平面\(β\)，\(γ\)都相交，则它们有\(2\)条交线，且这\(2\)条交线互相平行；
②若平面\(β∩\)平面\(γ=a\)，平面\(α\)是经过直线\(a\)的平面，则三个平面只有一条交线，即直线\(a\)；
③若平面\(β∩\)平面\(γ=a\)，平面\(α\)与平面\(β，γ\)都相交，但交线与直线\(a\)不重合，则它们有\(3\)条交线，例如棱柱或棱锥的三个侧面相交于三条直线，即三条侧棱
综上所述，这三个平面的交线的条数可能是\(1\)条、\(2\)条或\(3\)条
故选 \(D\)
【答案】 \(D\)
【解析】 如图，三个平面有一条交线的情况，

三个平面有两条交线的情况，

故选\(D\)．