5.1 任意角和弧度制
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【高分突破系列】高一数学上学期同步知识点剖析精品讲义与分层练习]
(https://www.zxxk.com/docpack/2783085.html)
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)
必修第一册同步拔高练习，难度3颗星！
模块导图
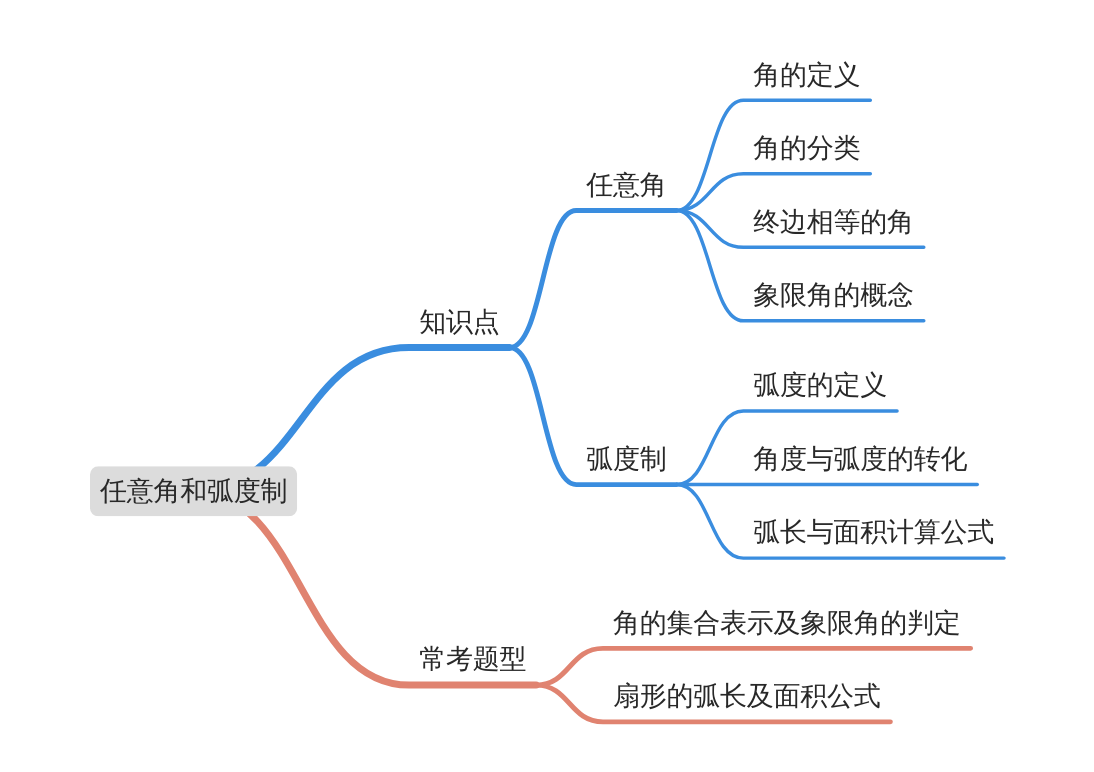
知识剖析
任意角
① 角的定义与分类
(1) 角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.
如下图，一条射线的端点是\(O\)，从起始位置\(OA\)按逆时针旋转到终止位置\(OB\)，形成角\(α\)，射线\(OA\) ，\(OB\)分别是角\(α\)的始边和终边.
(2) 逆时针旋转为正角，顺时针旋转为负角，不旋转为零角.
如下图\(\alpha=210^{\circ}\) ，\(\beta=-150^{\circ}\)，\(\gamma=-660^{\circ}\).
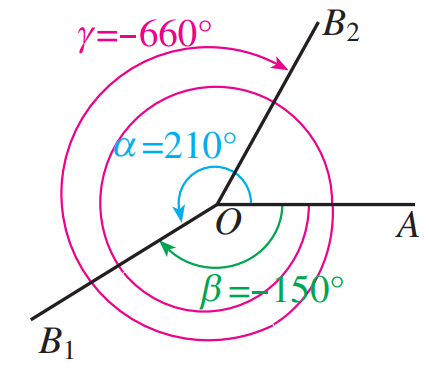
② 终边相等的角
与角\(α\)终边相同的角的集合为\(\left\{\beta \mid \beta=\alpha+k \cdot 360^{\circ}， k \in Z\right\}\).
注 表达式中的\(k∈ Z\)不能漏！
③ 象限角的概念
角\(α\)的顶点与原点重合，角的始边与\(x\)轴的非负半轴重合，终边落在第几象限，则称\(α\)为第几象限角.
注 \(α\)终边落在坐标轴上，不能称\(α\)为象限角.
弧度制
① 弧度的定义
弧长等于半径时，所对的圆心角为\(1\)弧度的圆心角，记作\(1 rad\).
即:半径为\(r\)的圆中，弧长为\(l\)的弧所对的圆心角为\(α rad\)，那么\(|\alpha|=\dfrac{l}{r}\).
② 角度与弧度的转化
\(180^{\circ}=\pi \Rightarrow 1^{\circ}=\dfrac{\pi}{180} \approx 0.01745\) \(1=\left(\dfrac{180}{\pi}\right)^{\circ} \approx 57.30^{\circ}\)
③ 特殊角的角度与弧度对应表
④ 弧长与扇形面积计算公式
弧长\(l=|α|\cdot R\)； 扇形面积\(S=\dfrac{1}{2} l R=\dfrac{1}{2} \alpha R^{2}\)，(\(R\)为圆的半径)
注 \(α\)为弧度制.
经典例题
【题型一】角的集合表示及象限角的判定
【典题1】 已知集合\(M=\{锐角\}\)，\(N=\{小于90^{\circ}的角\}\)，\(P=\{第一象限的角\}\)，下列说法：
① \(P⊆N\) ，\(\qquad \qquad\) ②\(N∩P=M\) ，
③ \(M⊆P\)， \(\qquad \qquad\) ④ \((M∪N)⊆P\).
其中正确的是\(\underline{\quad \quad}\)．
【解析】 锐角的范围为\(0^{\circ}<\theta<90^{\circ}\)，小于\(90^{\circ}\)角为\(\theta<90^{\circ}\)包含负角．
第一象限角为\(k \cdot 360^{\circ}<\theta<k \cdot 360^{\circ}+90^{\circ}， k \in Z\)，
\(∴P\)与\(N\)之间没有包含的关系，故①错；\(-300^{\circ} \in N \cap P\)，但\(-300^{\circ} \notin M\)，故②错；\(M∪N=N\)，不一定包含于\(P\)，故④错；③\(M⊆P\)对.
∴其中正确的是：③
【典题2】 写出如图所示阴影部分的角\(α\)的范围．
【解析】 (1)因为与\(45^{\circ}\)角终边相同的角可写成\(45^{\circ}+k \cdot 360^{\circ}， k \in Z\)的形式，
\(-180^{\circ}+30^{\circ}=-150^{\circ}\)角终边相同的角可写成\(-150^{\circ}+k \cdot 360^{\circ}， \quad k \in Z\)的形式，
所以图(1)阴影部分的角\(α\)的范围可表示为
\(\left\{\alpha \mid-150^{\circ}+k \cdot 360^{\circ}<\alpha \leq 45^{\circ}+k \cdot 360^{\circ}， k \in Z\right\}\)．
(2)因为与\(45^{\circ}\)角终边相同的角可写成\(45^{\circ}+k \cdot 360^{\circ}， k \in Z\)的形式，
\(360^{\circ}-60^{\circ}=300^{\circ}\)角终边相同的角可写成\(300^{\circ}+k \cdot 360^{\circ}， k \in Z\)的形式，
所以图(2)中角\(α\)的范围为\(\left\{\alpha \mid 45^{\circ}+k \cdot 360^{\circ} \leq \alpha \leq 300^{\circ}+k \cdot 360^{\circ}， k \in Z\right\}\)．
【点拨】表示与角\(α\)终边相同的角的集合时不要把\(k∈Z\)漏了.
【典题3】 若\(α\)是第三象限的角，则\(\dfrac{α}{3}\)可能是第\(\underline{\quad \quad}\) 象限角.
【解析】 方法1 不等式法
\(∵α\)是第三象限角，即\(2 k \pi+\pi<\alpha<2 k \pi+\dfrac{3}{2} \pi， k \in Z\)．
\(\dfrac{2 k \pi}{3}+\dfrac{\pi}{3} \leq \dfrac{\alpha}{3} \leq \dfrac{2 k \pi}{3}+\dfrac{\pi}{2}\)，(以下对\(k\)就被\(3\)除的余数分类讨论)
当\(k=3n ，n∈Z\)时，\(\dfrac{\alpha}{3} \in\left(2 n \pi+\dfrac{\pi}{3}， 2 n \pi+\dfrac{\pi}{2}\right)\)，\(\dfrac{α}{3}\)为第一象限角；
当\(k=3n+1 ，n∈Z\)时，\(\dfrac{\alpha}{3} \in\left(2 k \pi+\pi， 2 k \pi+\dfrac{7 \pi}{6}\right)\)，\(\dfrac{α}{3}\)为第三象限角．
当\(k=3n+2 ，n∈Z\)时，\(\dfrac{\alpha}{3} \in\left(2 k \pi+\dfrac{5 \pi}{3}， 2 k \pi+\dfrac{11 \pi}{6}\right)\)，\(\dfrac{α}{3}\)为第四象限角．
所以\(\dfrac{α}{3}\)可能是第一、三、四象限角.
方法2 八卦图法
先把直角坐标系每个象限平均分成\(3\)份，从x轴正半轴上方各区域标上\(1、2、3、4\)，找到标有\(α\)所在象限数字\(“3”\)所在的区域，该区域在哪个象限，则\(\dfrac{α}{3}\)的终边就在哪个象限.
故\(\dfrac{α}{3}\)可能是第一、三、四象限角.
【点拨】
① 方法1中令\(k=3n\)、\(3n+1\)、\(3n+2\)，\(n∈Z\)，是从\(3\)的余数\(“0、1、2”\)角度思考，故也可令\(k=0、1、2\).
② 方法2中的解题套路
判断\(\dfrac{α}{n}\)的象限
① 每个象限平分\(n\)份；② 从\(x\)轴上方逆时针开始标数；③ 找到\(α\)所在象限数字.
例：判断\(\dfrac{α}{3}\)的象限(\(α\)是第二象限的角)
① 每个象限平分\(3\)份； ② 从\(x\)轴上方逆时针开始标数； ③ 找到\(α\)所在象限数字\(“2”\).
【题型二】扇形的弧长及面积公式
【典题1】 \(-3\)弧度的角终边在第\(\underline{\quad \quad}\)象限.
【解析】 因为\(-\pi<-3<-\dfrac{\pi}{2}\)，所以\(-3\)弧度的角终边在第三象限．
【点拨】 \(1=\left(\dfrac{180}{\pi}\right)^{\circ} \approx 57.30^{\circ}\) ，则\(-3≈-171.9^°\).
【典题2】 已知\(2rad\)的圆心角所对的弦长为\(2\)，求这个圆心角所对的弧长．
【解析】 如图，
\(∠AOB=2\)，过\(O\)点作\(OC⊥AB\)于\(C\)，并延长\(OC\)交于\(D\).
\(∠AOD=∠BOD=1\)，且\(AC= AB=1\).
在\(Rt△AOC\)中，\(A O=\dfrac{A C}{\sin \angle A O C}=\dfrac{1}{\sin 1}\)，
从而弧\(AB\)的长为\(l=|\alpha| \cdot r=\dfrac{2}{\sin 1}\).
【典题3】 已知一扇形的中心角是\(α(α>0)\)，所在圆的半径是\(R\)．
(1)若\(α=60^∘\)，\(R=10cm\)，求扇形的弧所在的弓形面积；
(2)若扇形的周长是一定值\(c(c>0)\)，当\(α\)为多少弧度时，该扇形有最大面积？
【解析】 (1)设弧长为\(l\)，弓形面积为\(S_{\text {弓 }}\)，
\(\because \alpha=60^{\circ}=\dfrac{\pi}{3}， R=10\)，
\(\therefore S_{\text {扇 }}=\dfrac{1}{2} \alpha R^{2}=\dfrac{50 \pi}{3}\)，
\(\therefore S_{\text {弓 }}=S_{\text {扇 }}-S_{\triangle}\)\(=\dfrac{50 \pi}{3}-\dfrac{1}{2} \times 10 \times 10 \times \sin 60^{\circ}\)\(=\dfrac{50 \pi}{3}-25 \sqrt{3}\left(\mathrm{~cm}^{2}\right)\)．
(2)法一 ∵扇形周长\(c=2R+l=2R+αR\)，
\(\therefore R=\dfrac{c}{2+\alpha}\)，
\(\therefore S_{\text {扇 }}=\dfrac{1}{2} \alpha R^{2}=\dfrac{1}{2} \alpha\left(\dfrac{c}{2+\alpha}\right)^{2}\)\(=\dfrac{c^{2}}{2} \cdot \dfrac{\alpha}{4+4 \alpha+\alpha^{2}}=\dfrac{c^{2}}{2} \cdot \dfrac{1}{4+\alpha+\dfrac{4}{\alpha}}\)\(\leq \dfrac{c^{2}}{2} \cdot \dfrac{1}{4+4}=\dfrac{c^{2}}{16}\)．
(利用基本不等式)
\(∴\)当且仅当\(\alpha=\dfrac{4}{\alpha}\)，即\(α=2\)时，扇形面积有最大值\(\dfrac{c^{2}}{16}\)．
法二：由已知\(2R+l=c\)，
\(\therefore R=\dfrac{c-l}{2}(l<c)\)，
\(\therefore S=\dfrac{1}{2} R l=\dfrac{1}{2} \cdot \dfrac{c-l}{2} \cdot l\)\(=\dfrac{1}{4}\left(c l-l^{2}\right)=-\dfrac{1}{4}\left(l-\dfrac{c}{2}\right)^{2}+\dfrac{c^{2}}{16}\)，(二次函数最值问题)
\(∴\)当\(l=\dfrac{c}{2}\)时，\(S_{\max }=\dfrac{c^{2}}{16}\)，此时\(\alpha=\dfrac{l}{R}=2\)，
\(∴\)当扇形圆心角为\(2\)弧度时，扇形面积有最大值\(\dfrac{c^{2}}{16}\)．
【点拨】
① 弧长\(l=|α|\cdot R\)，扇形面积\(S=\dfrac{1}{2} l R=\dfrac{1}{2} \alpha R^{2}\) (\(R\)为圆的半径)；
② 求函数\(f(x)=\dfrac{a x}{b x^{2}+c x+d}\)最值，可把函数化简为\(f(x)=\dfrac{a}{b x+\dfrac{d}{x}+c}\)，再利用基本不等式求解.
巩固练习
1(★) 下列说法正确的是( )
A．终边相同的角相等 \(\qquad \qquad \qquad \qquad\) B．相等的角终边相同
C．小于\(90°\)的角是锐角 \(\qquad \qquad \qquad \qquad\) D．第一象限的角是正角
2(★) \(－870°\)的终边在第几象限 ( )
A．一 \(\qquad \qquad \qquad \qquad\) B．二 \(\qquad \qquad \qquad \qquad\) C．三 \(\qquad \qquad \qquad \qquad\) D．四
3(★) \(2100°\)化成弧度是 ( )
A．\(\dfrac{35}{3} \pi\) \(\qquad \qquad \qquad\)B．\(10π\) \(\qquad \qquad \qquad\) C．\(\dfrac{28}{3} \pi\) \(\qquad \qquad \qquad\)D．\(\dfrac{25}{3} \pi\)
4 (★★) 已知\(α\)是第二象限角，则\(\dfrac{\alpha}{2}\)是( )
A．锐角 \(\qquad \qquad \qquad\) B．第一象限角 \(\qquad \qquad \qquad\) C．第一、三象限角 \(\qquad \qquad \qquad\)D．第二、四象限角
5 (★★) 已知圆\(O\)与直线\(l\)相切于点\(A\)，点\(P ，Q\)同时从\(A\)点出发，\(P\)沿着直线\(l\)向右、\(Q\)沿着圆周按逆时针以相同的速度运动，当\(Q\)运动到点\(A\)时，点\(P\)也停止运动，连接\(OQ ，OP\)(如图)，则阴影部分面积\(S_1 ，S_2\)的大小关系是( )
A．\(S_1=S_2\)
B．\(S_1≤S_2\)
C．\(S_1≥S_2\)
D．先\(S_1<S_2\)，再\(S_1=S_2\)，最后\(S_1>S_2\)
6 (★★) 与\(－2014°\)终边相同的最小正角是\(\underline{\quad \quad}\) ．
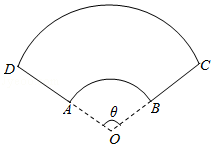
7 (★★) 中国扇文化有着深厚的文化底蕴，文人雅士喜在扇面上写字作画．如图，是书画家唐寅(1470－1523)的一幅书法扇面，其尺寸如图所示，则该扇面的面积为\(\underline{\quad \quad}\)\(cm^2\)．
8(★★) 已知圆锥的侧面展开图是一个半径为\(2cm\)，圆心角为\(\dfrac{2 \pi}{3}\)的扇形，则此圆锥的高为\(\underline{\quad \quad}\) \(cm\)．
挑战学霸
河南大学自招真题
我们知道当\(12\)点时，闹钟的\(3\)个指针完全重合，请说出除了\(12\)点外，是否还有其他时间，\(3\)针完全重合.如有请举出；若无，给出理由.
参考答案
- 【答案】 \(B\)
【解析】 终边相同的角相差周角的整数倍，\(A\)不正确；相等的角终边一定相同；所以\(B\)正确；小于\(90°\)的角是锐角可以是负角；第一象限的角是正角，也可以是负角．
故选：\(B\)． - 【答案】 \(C\)
【解析】 选\(C\)，因\(－870°=－2×360°－150°\).\(－150°\)是第三象限角． - 【答案】 \(A\)
【解析】 \(2100^{\circ}=2100 \times \dfrac{\pi}{180}=\dfrac{35 \pi}{3}\)．故选：\(A\)． - 【答案】 \(C\)
【解析】 \(∵α\)是第二象限角，所以\(\dfrac{\pi}{2}+2 k \pi<\alpha<\pi+2 k \pi\)，\(k∈Z\)，
\(\therefore \dfrac{\pi}{4}+k \pi<\dfrac{\alpha}{2}<k \pi+\dfrac{\pi}{2}\)，\(k∈Z\)，
\(\therefore \dfrac{\alpha}{2}\)是第一象限或第三象限角，故选：\(C\)． - 【答案】 \(A\)
【解析】 如图所示，
\(∵\)直线\(l\)与圆\(O\)相切，\(∴OA⊥AP\)，
\(\therefore S_{\text {扇形 } A O Q}=\dfrac{1}{2} \cdot \widehat{A Q} \cdot r=\dfrac{1}{2} \cdot \widehat{A Q} \cdot O A\)，\(S_{\triangle A O P}=\dfrac{1}{2} \cdot O A \cdot A P\)，
\(\because \widehat{A Q}=A P\)，
\(\therefore S_{\text {廂形 } A O Q}=S_{\triangle A O P}\)，即\(S_{\text {扇形 } A O Q}-S_{\text {扇形 } A O B}=S_{\triangle A O P}-S_{\text {扇形 } A O B}\)，
\(∴S_1=S_2\)
故选：\(A\)． - 【答案】 \(146°\)
【解析】 \(∵－2014°=－6×360°+146°\)，
\(∴146°\)与\(－2014°\)终边相同，又终边相同的两个角相差\(360°\)的整数倍，
\(∴\)在\([0°，360°)\)上，只有\(146°\)与\(－2014°\)终边相同，
\(∴\)与\(－2014°\)终边相同的最小正角是\(146°\)，
故答案为：\(146°\)． - 【答案】 \(704\)
【解析】 如图，设\(\angle A O B=\theta\)，\(OA=OB=r\)，
由题意可得\(\left\{\begin{array}{l} 24=r \theta \\ 64=(r+16) \theta \end{array}\right.\)，解得\(r=\dfrac{48}{5}\)，
所以\(S_{\text {扇面 }}=S_{\text {扇形OCD }}-S_{\text {扇形OAB }}=\dfrac{1}{2} \times 64 \times\left(\dfrac{48}{5}+16\right)-\dfrac{1}{2} \times 24 \times \dfrac{48}{5}=704 \mathrm{~cm}^{2}\)．
故答案为：\(704\)． - 【答案】 \(\dfrac{4 \sqrt{2}}{3}\)
【解析】 设此圆的底面半径为\(r\)，高为\(h\)，母线为\(l\)，
\(∵\)圆锥的侧面展开图是一个半径为\(2cm\)，圆心角为\(\dfrac{2 \pi}{3}\)的扇形，
\(∴l=2\)，得\(2 \pi r=\dfrac{2 \pi}{3} \times l=\dfrac{4 \pi}{3}\)，解之得\(r=\dfrac{2}{3}\)，
因此，此圆锥的高\(h=\sqrt{l^{2}-r^{2}}=\sqrt{2^{2}-\left(\dfrac{2}{3}\right)^{2}}=\dfrac{4 \sqrt{2}}{3} \mathrm{~cm}\)．
故答案为：\(\dfrac{4 \sqrt{2}}{3}\)．
【挑战学霸】
解 每小时时针、分针旋转一次，速度为时针\(0.5^{\circ} / \mathrm{min}\)，分针\(6^{\circ} / \min\)相差\(5.5^{\circ} / \mathrm{min}\)，故在\(n\)时\(00\)分至\((n+1)\)时\(00\)分之间，时针和分针完全重合的时刻为\(n\)时\(\dfrac{60 n}{11}\)分，它们是：
1时5分27.27秒 2时10分54.54秒 3时16分21.82秒 4时21分49.09秒
5时27分16.36秒 6时32分43.64秒 7时38分10.91秒 8时43分38.18秒
9时49分5.45秒 10时54分32.73秒 12时00分00秒
这些时刻里除了\(12\)时外，“分”和“秒“的值相差都很大，分针和秒针显然不可能重合.所以仅在\(12\)时三针重合.
