1.2 空间向量基本定理
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学上学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
选择性必修第一册同步提高,难度3颗星!
知识剖析
空间向量基本定理
如果三个向量\(\vec{a}\),\(\vec{b}\) ,\(\vec{c}\)不共面,那么对空间任一向量\(\vec{p}\),存在一个唯一的有序实数组\(x\) ,\(y\) ,\(z\),使\(\vec{p}=x \vec{a}+y \vec{b}+z \vec{c}\).
证明
存在性 设\(\vec{a}\),\(\vec{b}\) ,\(\vec{c}\)不共面,过点\(O\)作\(\overrightarrow{O A}=\vec{a}\), \(\overrightarrow{O B}=\vec{b}\), \(\overrightarrow{O C}=\vec{c}\),\(\overrightarrow{O P}=\vec{p}\),
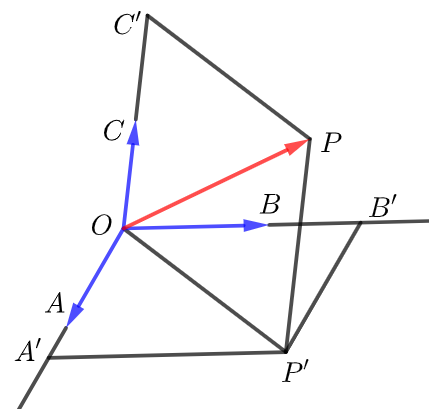
过点\(P\)作直线\(PP'\)平行于\(OC\)交平面\(OAB\)于点\(P'\)在平面\(OAB\)内,
过点\(P'\)作直线\(P' A'//OB\),\(P' B'//OA\),
存在三个数\(x\),\(y\),\(z\),使得\(\overrightarrow{OA'}=x \overrightarrow{O A}=x\vec{a}\),\(\overrightarrow{OB'}=y \overrightarrow{O B}=y\vec{b}\),\(\overrightarrow{O C'}=z \overrightarrow{O C}=z\vec{c}\),
\(\therefore \overrightarrow{O P}=\overrightarrow{O A^{\prime}}+\overrightarrow{O B^{\prime}}+\overrightarrow{O C^{\prime}}=x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C}\),
\(\therefore \vec{p}=x\vec{a}+y\vec{b} +z\vec{c}\);
唯一性设另有一组实数\(x'\),\(y'\),\(z'\),使得\(\vec{p}=x'\vec{a}+y'\vec{b} +z'\vec{c}\),
则\(x\vec{a}+y\vec{b} +z\vec{c}=x'\vec{a}+y'\vec{b} +z'\vec{c}\),
\(\therefore (x-x' ) \vec{a}+(y-y' ) \vec{a}+(z-z' ) \vec{c}=\vec{0}\),
\(\because \vec{a}\),\(\vec{b}\) ,\(\vec{c}\)不共面,\(\therefore x-x'=y-y'=z-z'=0\),
即\(x=x'\)且\(y=y'\)且\(z=z'\).
故实数\(x\) ,\(y\) ,\(z\)是唯一的.
基底
若三向量\(\vec{a}\),\(\vec{b}\) ,\(\vec{c}\)不共面,我们把\((\vec{a}, \vec{b}, \vec{c})\)叫做空间的一个基底, \(\vec{a}\),\(\vec{b}\) ,\(\vec{c}\)叫做基向量,空间任意三个不共面的向量都可以构成空间的一个基底.
特别地,如果空间的一个基底中的三个基向量两两垂直,且长度都为\(1\),那么这个基底叫做单位正交基底,常用\(\{\vec{i},\vec{j},\vec{k}\}\)表示.由 基本定理可知,对空间中的任意向量\(\vec{a}\),均可以分解为三个向量\(x\vec{i}\),\(y\vec{j}\),\(z\vec{k}\),使\(\vec{a}=x\vec{i}+y\vec{j}+z\vec{k}\),像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
推论
设\(O\),\(A\),\(B\),\(C\)是不共面的四点,则对空间任一点\(P\),都存在唯一的三个有序实数\(x\) ,\(y\) ,\(z\),使\(\overrightarrow{O P}=x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C}\).
若\(x+y+z=1\),则点\(P\),\(A\),\(B\),\(C\)四点共面.
经典例题
【题型一】 空间向量基本定理的理解
【典题1】 若\(\{\vec{a},\vec{b},\vec{c}\}\)构成空间的一个基底,则下列向量能构成空间的一个基底的是( )
A.\(\vec{b}+\vec{c}\),\(\vec{b}\),\(\vec{b}-\vec{c}\) \(\qquad \qquad \qquad \qquad\) B.\(\vec{a}+\vec{b}\),\(\vec{a}-\vec{b}\),\(\vec{c}\)
C.\(\vec{a}\),\(\vec{a}+\vec{b}\),\(\vec{a}-\vec{b}\) \(\qquad \qquad \qquad \qquad\) D.\(\vec{a}+\vec{b}\),\(\vec{a}+\vec{b}+\vec{c}\),\(\vec{c}\)
【解析】 对于\(A\),若向量\(\vec{b}+\vec{c}\),\(\vec{b}\),\(\vec{b}-\vec{c}\)共面,
则\(\vec{b}+\vec{c}=\lambda (\vec{b}-\vec{c})+\mu\vec{b}=(\lambda +\mu)\vec{b}-\lambda \vec{c}\),
即 \(\left\{\begin{array}{l}
\lambda+\mu=1 \\
-\lambda=1
\end{array}\right.\),解得\(\lambda =-1\),\(\mu=2\),
故向量\(\vec{b}+\vec{c}\),\(\vec{b}\),\(\vec{b}-\vec{c}\)共面,故\(A\)错误,
对于\(B\),若向量\(\vec{a}+\vec{b}\),\(\vec{a}-\vec{b}\),\(\vec{c}\)共面,
则\(\vec{a}+\vec{b}=\lambda (\vec{a}-\vec{b})+\mu\vec{c}\),\(\lambda\),\(\mu\)无解,
故向量\(\vec{a}+\vec{b}\),\(\vec{a}-\vec{b}\),\(\vec{c}\)不共面,故\(B\)正确,
对于\(C\),若向量\(\vec{a}\),\(\vec{a}+\vec{b}\),\(\vec{a}-\vec{b}\)共面,
则\(\vec{a}+\vec{b}=\lambda \vec{a}+\mu(\vec{a}-\vec{b})=(\lambda +\mu)\vec{a}-\mu\vec{b}\),
即 \(\left\{\begin{array}{l}
\lambda+\mu=1 \\
-\mu=1
\end{array}\right.\),解得\(\lambda =2\),\(\mu=-1\),
故向量\(\vec{a}\),\(\vec{a}+\vec{b}\),\(\vec{a}-\vec{b}\)共面,故\(C\)错误,
对于\(D\),若向量\(\vec{a}+\vec{b}\),\(\vec{a}+\vec{b}+\vec{c}\),\(\vec{c}\)共面,
则\(\vec{a}+\vec{b}+\vec{c}=\lambda (\vec{a}+\vec{b})+\mu\vec{c}\),解得\(\lambda =\mu=1\),
故向量\(\vec{a}+\vec{b}\),\(\vec{a}+\vec{b}+\vec{c}\),\(\vec{c}\)共面,故\(D\)错误.
故选:\(B\).
【典题2】 已知非零向量\(\vec{a}=3\vec{m}-2\vec{n}-4\vec{p}\),\(\vec{b}=(x+1)\vec{m}+8\vec{n}+2y\vec{p}\),且\(\vec{m}\)、\(\vec{n}\)、\(\vec{p}\)不共面.若\(\vec{a}//\vec{b}\),则\(x+y=\)\(\underline{\quad \quad}\) .
【解析】 \(\because\vec{m}\)、\(\vec{n}\)、\(\vec{p}\)不共面,故\(\vec{m}\)、\(\vec{n}\)、\(\vec{p}\)可看作空间向量的一组基底,
\(\because \vec{a}//\vec{b}\),故存在\(\lambda ≠0\),使得\(\vec{b}=\lambda \vec{a}\),
即\((x+1)\vec{m}+8\vec{n}+2y\vec{p}=3\lambda \vec{m}-2\lambda \vec{n}-4\lambda \vec{p}\),
\(\therefore\left\{\begin{array}{l}
x+1=3 \lambda \\
8=-2 \lambda \\
2 y=-4 \lambda
\end{array}\right.\),解得: \(\left\{\begin{array}{l}
x=-13 \\
y=8
\end{array}\right.\),则\(x+y=-5\).
【典题3】 如图,在三棱锥\(S-ABC\)中,点\(E\),\(F\)分别是\(SA\),\(BC\)的中点,点\(G\)在棱\(EF\)上,且满足\(\dfrac{E G}{G F}=\dfrac{1}{2}\),若\(\overrightarrow{SA}=\vec{a}\),\(\overrightarrow{SB}=\vec{b}\),\(\overrightarrow{SC}=\vec{c}\),则\(\overrightarrow{SG}=\) ( )

A.\(\dfrac{1}{3} \vec{a}-\dfrac{1}{2}\vec{b}+\dfrac{1}{6} \vec{c}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{1}{3} \vec{a}+\dfrac{1}{6} \vec{b}+\dfrac{1}{6} \vec{c}\)
C.\(\dfrac{1}{6} \vec{a}-\dfrac{1}{3} \vec{b}+\dfrac{1}{2}\vec{c}\) \(\qquad \qquad \qquad \qquad\) D.\(\dfrac{1}{3} \vec{a}-\dfrac{1}{6} \vec{b}+\dfrac{1}{2}\vec{c}\)
【解析】 因为\(\overrightarrow{SG}=\overrightarrow{SE}+\overrightarrow{EG}=\dfrac{1}{2}\overrightarrow{SA}+\dfrac{1}{3} \overrightarrow{EF}=\dfrac{1}{2}\overrightarrow{SA}+\dfrac{1}{3}(\overrightarrow{ES}+\overrightarrow{SC}+\overrightarrow{CF})\)\(=\dfrac{1}{2}\overrightarrow{SA}+\dfrac{1}{6} (AS) ⃗+\dfrac{1}{3} \overrightarrow{SC}+\dfrac{1}{6} \overrightarrow{CB}=\dfrac{1}{3} \overrightarrow{SA}+\dfrac{1}{3} \overrightarrow{SC}+\dfrac{1}{6}(\overrightarrow{CS}+\overrightarrow{SB})\)
\(=\dfrac{1}{3} \overrightarrow{SA}+\dfrac{1}{6} \overrightarrow{SB}+\dfrac{1}{6} \overrightarrow{SC}=\dfrac{1}{3} \vec{a}+\dfrac{1}{6} \vec{b}+\dfrac{1}{6} \vec{c}\).
故选:\(B\).
巩固练习
1(★) 已知\(O\),\(A\),\(B\),\(C\)为空间四点,且向量\(\overrightarrow{O A}\), \(\overrightarrow{O B}\), \(\overrightarrow{O C}\)不能构成空间的一个基底,则一定有( )
A.\(\overrightarrow{O A}\),\(\overrightarrow{O B}\),\(\overrightarrow{O C}\)共线
B.\(O\),\(A\),\(B\),\(C\)中至少有三点共线
C.\(\overrightarrow{O A}+ \overrightarrow{O B}\)与\(\overrightarrow{O C}\)共线
D.\(O\),\(A\),\(B\),\(C\)四点共面
2(★) (多选题)下面四个结论正确的是( )
A.空间向量\(\vec{a}\),\(\vec{b}(\vec{a}≠\vec{0},\vec{b}≠\vec{0})\),若\(\vec{a}⊥\vec{b}\),则\(\vec{a}\cdot \vec{b}=0\)
B.若对空间中任意一点\(O\),有\(\overrightarrow{O P}=\dfrac{1}{6} \overrightarrow{O A}+\dfrac{1}{3} \overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O C}\),则\(P\),\(A\),\(B\),\(C\)点共面
C.已知\(\{\vec{a},\vec{b},\vec{c}\}\)是空间的一组基底,若\(\vec{m}=\vec{a}+\vec{c}\),则\(\{\vec{a},\vec{b},\vec{m}\}\)也是空间的一组基底
D.任意向量\(\vec{a}\),\(\vec{b}\),\(\vec{c}\)满足\((\vec{a}\cdot \vec{b})\cdot \vec{c}=\vec{a}\cdot (\vec{b}\cdot \vec{c}) \vec{a}\cdot \vec{b}=0\)
3(★★) 如图所示,在四面体\(O-ABC\)中, \(\overrightarrow{O A}=\vec{a}\), \(\overrightarrow{O B}=\vec{b}\), \(\overrightarrow{O C}=\vec{c}\),点\(M\)在\(OA\)上,且\(\overrightarrow{OM}=2\overrightarrow{MA}\),\(N\)为\(BC\)的中点,则\(\overrightarrow{MN}=\) ( )

A.\(\dfrac{1}{2}\vec{a}-\dfrac{2}{3} \vec{b}+\dfrac{1}{2}\vec{c}\) \(\qquad \qquad \qquad \qquad\) B.\(-\dfrac{2}{3} \vec{a}+\dfrac{1}{2}\vec{b}+\dfrac{1}{2}\vec{c}\)
C.\(\dfrac{1}{2}\vec{a}+\dfrac{1}{2}\vec{b}-\dfrac{2}{3} \vec{c}\) \(\qquad \qquad \qquad \qquad\) D.\(\dfrac{2}{3} \vec{a}+\dfrac{2}{3} \vec{b}-\dfrac{1}{2}\vec{c}\)
参考答案
-
【答案】 \(D\)
【解析】 由于向量\(\overrightarrow{O A}\),\(\overrightarrow{O B}\),\(\overrightarrow{O C}\)不能构成空间的一个基底知 \(\overrightarrow{O A}\),\(\overrightarrow{O B}\),\(\overrightarrow{O C}\)共面,
所以\(O\),\(A\),\(B\),\(C\)四点共面,故选:\(D\). -
【答案】 \(ABC\)
【解析】 对于\(A\):空间向量\(\vec{a}\),\(\vec{b}(\vec{a}≠\vec{0},\vec{b}≠\vec{0})\),若\(\vec{a}⊥\vec{b}\),则 ,故\(A\)正确;
对于\(B\):若对空间中任意一点\(O\),有 \(\overrightarrow{O P}=\dfrac{1}{6} \overrightarrow{O A}+\dfrac{1}{3} \overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O C}\),
由于\(\dfrac{1}{6}+\dfrac{1}{2}+\dfrac{1}{3}=1\),则\(P\),\(A\),\(B\),\(C\)四点共面,故\(B\)正确;
对于\(C\):已知\(\{\vec{a},\vec{b},\vec{c}\}\)是空间的一组基底,若\(\vec{m}=\vec{a}+\vec{c}\),
则\(\{\vec{a},\vec{b},\vec{a}+\vec{c}\}\)两向量之间不共线,故也是空间的一组基底,故\(C\)正确;
对于\(D\):任意向量\(\vec{a}\),\(\vec{b}\),\(\vec{c}\)满足\((\vec{a}\cdot \vec{b})\cdot \vec{c}=\vec{a}\cdot (\vec{b}\cdot \vec{c})\),由于\(\vec{a}\cdot \vec{b}\)是一个数值,\(\vec{b}\cdot \vec{c}\)也是一个数值,则说明\(\vec{c}\)和\(\vec{a}\)存在倍数关系,由于\(\vec{a}\),\(\vec{b}\),\(\vec{c}\)是任意向量,不一定存在倍数关系,故\(D\)错误.
故选:\(ABC\). -
【答案】 \(B\)
【解析】 连接\(ON\),
\(\because N\)是\(BC\)的中点,\(\therefore \overrightarrow{ON}=\dfrac{1}{2} \overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O C}\),
\(\because \overrightarrow{OM}=2\overrightarrow{MA}\),\(\therefore \overrightarrow{OM}=\dfrac{2}{3} \overrightarrow{O A}\),
\(\therefore \overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM}=\dfrac{1}{2} \overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O C}-\dfrac{2}{3} \overrightarrow{O A}=-\dfrac{2}{3} \vec{a}+\dfrac{1}{2}\vec{b}+\dfrac{1}{2}\vec{c}\),
故选:\(B\).

【题型二】空间向量基本定理的应用
【典题1】 如图,平行六面体\(ABCD-A_1 B_1 C_1 D_1\)的底面\(ABCD\)是菱形,且\(∠C_1 CB=∠C_1 CD=∠BCD=60^{\circ}\),\(CD=CC_1\),求证\(CA_1⊥\)平面\(C_1 BD\).

【证明】 如图,设\(CD=CB=CC_1=a\),
令\(\overrightarrow{CD}=\vec{a}\),\(\overrightarrow{CB}=\vec{b}\),\(\overrightarrow{CC_1 }=\vec{c}\),
则\(\overrightarrow{BD }=\vec{a}-\vec{b},
\overrightarrow{CA_1 }=\overrightarrow{CD}+\overrightarrow{CB}+\overrightarrow{CC_1 }=\vec{a}+\vec{b}+\vec{c}\),
\(\therefore \overrightarrow{CA_1 }\cdot \overrightarrow{BD }=(\vec{a}+\vec{b}+\vec{c} )(\vec{a}-\vec{b} )\)\(=\vec{a}\cdot \vec{a}-\vec{a}\cdot \vec{b}+\vec{b}\cdot \vec{a}-\vec{b}\cdot \vec{b}+\vec{c}\cdot \vec{a}-\vec{c}\cdot \vec{b}\),
又\(\vec{a}\cdot \vec{a}=\vec{b}\cdot \vec{b}=\vec{c}\cdot \vec{c}=a^2,\vec{a}\cdot \vec{b}=\vec{b}\cdot \vec{c}=\vec{a}\cdot \vec{c}=\dfrac{1}{2}a^2\),
\(\therefore \overrightarrow{CA_1 }\cdot \overrightarrow{BD }=0\),\(\therefore \overrightarrow{CA_1 }⊥\overrightarrow{BD }\),\(\therefore CA_1⊥BD\),
同理可证\(CA_1⊥C_1 B\),
又\(C_1 B∩BD=B\),\(C_1 B\),\(BD⊂\)平面\(C_1 BD\),
\(\therefore CA_1⊥\)平面\(C_1 BD\).
【典题2】 如图,在三棱锥\(P-ABC\)中,点\(G\)为\(△ABC\)的重心,点\(M\)在\(PG\)上,且\(PM=3MG\),过点\(M\)任意作一个平面分别交线段\(PA\),\(PB\),\(PC\)于点\(D\),\(E\),\(F\),若\(\overrightarrow{PD}=m\overrightarrow{PA}\),\(\overrightarrow{PE}=n\overrightarrow{PB}\),\(\overrightarrow{PF}=t\overrightarrow{PC}\),求证: \(\dfrac{1}{m}+\dfrac{1}{n}+\dfrac{1}{t}\)为定值,并求出该定值.

【证明】 如图示:
连接\(AG\)并延长交\(BC\)于点\(H\),
由题意可令\(\{\overrightarrow{PA},\overrightarrow{PB},\overrightarrow{PC}\}\)为空间的一个基底,
故\(\overrightarrow{PM}=\dfrac{3}{4}\overrightarrow{PG}=\dfrac{3}{4}(\overrightarrow{PA}+\overrightarrow{AG})=\dfrac{3}{4} \overrightarrow{PA}+\dfrac{3}{4}\cdot \dfrac{2}{3} \overrightarrow{AH}\)
\(=\dfrac{3}{4} \overrightarrow{PA}+\dfrac{1}{2}\cdot \dfrac{1}{2}(\overrightarrow{AB }+\overrightarrow{AC})\)\(=\dfrac{3}{4} \overrightarrow{PA}+\dfrac{1}{4}(\overrightarrow{PB}-\overrightarrow{PA})+\dfrac{1}{4}(\overrightarrow{PC}-\overrightarrow{PA})\)\(=\dfrac{1}{4} \overrightarrow{PA}+\dfrac{1}{4} \overrightarrow{PB}+\dfrac{1}{4} \overrightarrow{PC}\),
连接\(DM\),因为点\(D\),\(E\),\(F\),\(M\)共面,
故存在实数\(\lambda\),\(\mu\),使得\(\overrightarrow{DM}=\lambda \overrightarrow{DE}+\mu\overrightarrow{DF }\),
即\(\overrightarrow{PM}-\overrightarrow{PD}=\lambda (\overrightarrow{PE}-\overrightarrow{PD})+\mu(\overrightarrow{PF}-\overrightarrow{PD})\),
故\(\overrightarrow{P M}=(1-\lambda-\mu) \overrightarrow{P D}+\lambda \overrightarrow{P E}+\mu \overrightarrow{P F}\)\(=(1-\lambda-\mu) m \overrightarrow{P A}+\lambda n \overrightarrow{P B}+\mu t \overrightarrow{P C}\),
由空间向量基本定理知\(\dfrac{1}{4}=(1-\lambda -\mu)m\),\(\dfrac{1}{4}=\lambda n\),\(\dfrac{1}{4}=\mu t\),
故 \(\dfrac{1}{m}+\dfrac{1}{n}+\dfrac{1}{t}=4(1-\lambda-\mu)+4 \lambda+4 \mu=4\),为定值.

巩固练习
1(★★) 如图,三棱柱\(ABC-A_1 B_1 C_1\)的所有棱长都相等,\(∠A_1 AB=∠A_1 AC=60^{\circ}\),点\(M\)为\(△ABC\)的重心,\(AM\)的延长线交\(BC\)于点\(N\),连接\(A_1 M\).设\(\overrightarrow{AB }=\vec{a}\),\(\overrightarrow{AC}=\vec{b}\), \(\overrightarrow{A_1 A}=\vec{c}\).
(1)用\(\vec{a}\),\(\vec{b}\),\(\vec{c}\)表示\(\overrightarrow{A_1 M}\); \(\qquad \qquad\) (2)证明:\(A_1 M⊥AB\).

2(★★) 如图,在棱长为\(1\)的正方体\(ABCD-A_1 B_1 C_1 D_1\)中, \(E\),\(F\)分别为\(DD_1\),\(BD\) 的中点,点\(G\) 在\(CD\)上,且\(CG=\dfrac{1}{4} CD\).
(1) 求证: \(EF⊥B_1 C\); \(\qquad \qquad\) (2) 求\(EF\)与\(C_1 G\) 所成角的余弦值.

3(★★★) 如图,在底面\(ABCD\)为菱形的平行六面体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M\),\(N\)分别在棱\(AA_1\),\(CC_1\)上,且\(A_1 M=\dfrac{1}{3} AA_1\),\(CN=\dfrac{1}{3} CC_1\),且\(∠A_1 AD=∠A_1 AB=∠DAB=60^{\circ}\).
(1)用向量\(\overrightarrow{AA_1 }\),\(\overrightarrow{AD }\),\(\overrightarrow{AB }\)表示向量\(\overrightarrow{MN}\);
(2)求证:\(D\),\(M\),\(B_1\),\(N\)共面;
(3)当 \(\dfrac{A A_1}{A B}\)为何值时,\(AC_1⊥A_1 B\).

4(★★★) 已知四面体中三组相对棱的中点间的距离都相等, 求证: 这个四面体相对的棱丙两垂直.
已知:如图,四面体\(ABCD\),\(E\),\(F\),\(G\),\(H\),\(K\),\(M\)分别为棱\(AB\),\(BC\),\(CD\),\(DA\),\(BD\),\(AC\)的中点,且\(|EG|=|FH|=|KM|\).

求证 \(AB⊥CD\),\(AC⊥BD\),\(AD⊥BC\).
5(★★★) 已知正三棱锥\(P-ABC\)的侧棱长为\(2\),过其底面中心\(O\)作动平面\(α\)交线段\(PC\)于点\(S\),分别交\(PA\),\(PB\)的延长线于点\(M\),\(N\),求\(\dfrac{1}{P S}+\dfrac{1}{P M}+\dfrac{1}{P N}\)的值.

参考答案
-
【答案】 (1) \(\overrightarrow{A_1 M}=\dfrac{1}{3} \vec{a}+\dfrac{1}{3} \vec{b}+\vec{c}\)(2)略
【解析】 (1)因为\(△ABC\)为正三角形,点\(M\)为\(△ABC\)的重心,所以\(N\)为\(BC\)的中点,
所以 \(\overrightarrow{A N}=\dfrac{1}{2} \overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{A C}\), \(\overrightarrow{A M}=\dfrac{2}{3} \overrightarrow{A N}\),
所以 \(\overrightarrow{A_1 M}=\overrightarrow{A_1 A}+\overrightarrow{A M}=-\overrightarrow{A A_1}+\dfrac{2}{3} \overrightarrow{A N}\)
\(=-\overrightarrow{A A}_1+\dfrac{1}{3} \overrightarrow{A B}+\dfrac{1}{3} \overrightarrow{A C}=\dfrac{1}{3} \vec{a}+\dfrac{1}{3} \vec{b}+\vec{c}\).
(2)设三棱柱的棱长为\(m\),
则 \(\overrightarrow{A_1 M} \cdot \overrightarrow{A B}=\left(\dfrac{1}{3} \vec{a}+\dfrac{1}{3} \vec{b}+\vec{c}\right) \cdot \vec{a}=\dfrac{1}{3} \vec{a}^2+\dfrac{1}{3} \vec{a} \cdot \vec{b}+\vec{c} \cdot \vec{a}\)\(=\dfrac{1}{3} m^2+\dfrac{1}{3} m^2 \times \dfrac{1}{2}-m^2 \times \dfrac{1}{2}=0\),
所以\(A_1 M⊥AB\). -
【答案】 (1) 略 (2) \(\dfrac{\sqrt{51}}{17}\)
【解析】 (1)证明 设\(\overrightarrow{DA}=\vec{a}\),\(\overrightarrow{DC}=\vec{b}\),\(\overrightarrow{DD_1 }=\vec{c}\),
则\(\overrightarrow{EF}=\overrightarrow{DF }-\overrightarrow{DE}=\dfrac{1}{2}\overrightarrow{DB}-\dfrac{1}{2}\overrightarrow{DD_1 }=\dfrac{1}{2}(\overrightarrow{DA}+\overrightarrow{DC})-\dfrac{1}{2}\overrightarrow{DD_1 }\)\(=\dfrac{1}{2}(\vec{a}+\vec{b})-\dfrac{1}{2}\vec{c}=\dfrac{1}{2}(\vec{a}+\vec{b}-\vec{c})\)
\(\overrightarrow{B_1 C}=\overrightarrow{A_1 D}=-\overrightarrow{D A_1}=-\left(\overrightarrow{D A}+\overrightarrow{D D}_1\right)=-(\vec{a}+\vec{c})\),
\(\because \overrightarrow{EF}\cdot \overrightarrow{B_1 C}=\dfrac{1}{2}(\vec{a}+\vec{b}-\vec{c} )\cdot [-(\vec{a}+\vec{c} )]\)
\(=-\dfrac{1}{2}(\vec{a}^2+\vec{a}\cdot \vec{c}+\vec{a}\cdot \vec{b}+\vec{b}\cdot \vec{c}-\vec{a}\cdot \vec{c}-\vec{c}^2 )\)
\(=-\dfrac{1}{2}(1+0+0+0-0-1)=0\),
\(\therefore \overrightarrow{EF}⊥\overrightarrow{B_1 C}\),\(\therefore EF⊥B_1 C\).
(2)解 由(1)知\(\overrightarrow{EF}=\dfrac{1}{2}(\vec{a}+\vec{b}-\vec{c})\),
\(\overrightarrow{GC}_1=\overrightarrow{GC}+\overrightarrow{CC_1 }=\dfrac{1}{4} \overrightarrow{DC}+\overrightarrow{CC_1 }=\dfrac{1}{4} \vec{b}+\vec{c}\),
又 \(|\overrightarrow{E F}|=\dfrac{\sqrt{3}}{2}\), \(\left|\overrightarrow{G C_1}\right|=\dfrac{\sqrt{17}}{4}\),
\(\overrightarrow{E F} \cdot \overrightarrow{G C_1}=\dfrac{1}{2}(\vec{a}+\vec{b}-\vec{c}) \cdot\left(\dfrac{1}{4} \vec{b}+\vec{c}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{4} \vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}+\dfrac{1}{4} \vec{b}^2+\vec{b} \cdot \vec{c}-\dfrac{1}{4} \vec{b} \cdot \vec{c}-\vec{c}^2\right)\)\(=\dfrac{1}{2}\left(0+0+\dfrac{1}{4}+0-0-1\right)=\dfrac{1}{2} \times\left(-\dfrac{3}{4}\right)=-\dfrac{3}{8}\),
\(\cos \left\langle\overrightarrow{E F}, \overrightarrow{G C_1}\right\rangle=\dfrac{\overrightarrow{E F} \cdot \overrightarrow{G C_1}}{|\overrightarrow{E F} \|| \overrightarrow{G C_1} \mid}=\dfrac{-\dfrac{3}{8}}{\dfrac{\sqrt{3}}{2} \times \dfrac{\sqrt{17}}{4}}=-\dfrac{\sqrt{51}}{17}\),
\(\therefore EF\)与\(C_1 G\)所成角的余弦值为 \(\dfrac{\sqrt{51}}{17}\). -
【答案】 (1)\(\overrightarrow{MN}=\overrightarrow{AB }+\overrightarrow{AD }-\dfrac{1}{3} \overrightarrow{AA_1 }\) (2)略 (3)\(1\)
【解析】 (1)\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AB }+\overrightarrow{BC }+\overrightarrow{CN }=-\dfrac{2}{3} \overrightarrow{AA_1 }+\overrightarrow{AB }+\overrightarrow{BC }+\dfrac{1}{3} \overrightarrow{AA_1 }\)\(=\overrightarrow{AB }+\overrightarrow{AD }-\dfrac{1}{3} \overrightarrow{AA_1 }\).
证明:(2) \(\because \overrightarrow{D M}=\overrightarrow{A M}-\overrightarrow{A D}=\dfrac{2}{3} \overrightarrow{A A_1}-\overrightarrow{A D}\),\(\overrightarrow{N B_1}=\overrightarrow{C_1 B_1}-\overrightarrow{C_1 N}=\dfrac{2}{3} \overrightarrow{A A_1}-\overrightarrow{A D}\),
\(\therefore \overrightarrow{D M}=\overrightarrow{N B_1}\),\(\therefore D\),\(M\),\(B_1\),\(N\)共面.
解:(3)当 \(\dfrac{A A_1}{A B}=1\),\(AC_1⊥A_1 B\),
证明:设\(\overrightarrow{AA_1 }=\vec{c}\),\(\overrightarrow{AD }=\vec{b}\),\(\overrightarrow{AB }=\vec{a}\),
\(\because\)底面\(ABCD\)为菱形,则当\(\dfrac{A A_1}{A B}=1\)时,\(|\vec{a}|=|\vec{b}|=|\vec{c}|\),
\(\because \overrightarrow{AC_1 }=\overrightarrow{AB }+\overrightarrow{BC }+\overrightarrow{CC_1 }=\vec{a}+\vec{b}+\vec{c}\), \(\overrightarrow{A_1 B}=\overrightarrow{A B}-\overrightarrow{A A_1}=\vec{a}-\vec{c}\),
\(\angle A_1 A D=\angle A_1 A B=\angle D A B=60^{\circ}\),\(\therefore \overrightarrow{A C_1} \cdot \overrightarrow{A_1 B}=(\vec{a}+\vec{b}+\vec{c}) \cdot(\vec{a}-\vec{c})=\vec{a}^2+\vec{a} \cdot \vec{b}-\vec{b} \cdot \vec{c}-\vec{c}^2=0\),
\(\therefore AC_1⊥A_1 B\). -
证明 设\(\overrightarrow{AB }=\vec{a}\),\(\overrightarrow{AC}=\vec{b}\),\(\overrightarrow{AD }=\vec{c}\),
则\(\overrightarrow{EG}=\overrightarrow{AG}-\overrightarrow{AE}=\dfrac{1}{2}(\overrightarrow{AC}+\overrightarrow{AD })-\dfrac{1}{2}\overrightarrow{AB }\)\(=-\dfrac{1}{2}\vec{a}+\dfrac{1}{2}\vec{b}+\dfrac{1}{2}\vec{c}=\dfrac{1}{2}(-\vec{a}+\vec{b}+\vec{c})\),
\(\overrightarrow{FH}=\overrightarrow{AH}-\overrightarrow{AF}=\dfrac{1}{2}\overrightarrow{AD }-\dfrac{1}{2}(\overrightarrow{AB }+\overrightarrow{AC})\)\(=\dfrac{1}{2}\vec{c}-\dfrac{1}{2}(\vec{a}+\vec{b})=\dfrac{1}{2}(-\vec{a}-\vec{b}+\vec{c})\),
\(\overrightarrow{KM}=\overrightarrow{AM}-\overrightarrow{AK}=\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}(\overrightarrow{AB }+\overrightarrow{AD })\)\(=\dfrac{1}{2}\vec{b}-\dfrac{1}{2}(\vec{a}+\vec{c})=\dfrac{1}{2}(-\vec{a}+\vec{b}-\vec{c})\),
\(\because |\overrightarrow{EG}|=|\overrightarrow{FH}|\),\(\therefore |\dfrac{1}{2}(-\vec{a}+\vec{b}+\vec{c})|=|\dfrac{1}{2}(-\vec{a}-\vec{b}+\vec{c})|\)
\(\therefore (-\vec{a}+\vec{b}+\vec{c})^2=(-\vec{a}-\vec{b}+\vec{c})^2\),
\(\therefore \vec{a}^2+\vec{b}^2+\vec{c}^2-2\vec{a}\cdot \vec{b}-2\vec{a}\cdot \vec{c}+2\vec{b}\cdot \vec{c}\)\(=\vec{a}^2+\vec{b}^2+\vec{c}^2+2\vec{a}\cdot \vec{b}-2\vec{a}\cdot \vec{c}-2\vec{b}\cdot \vec{c}\),
\(\therefore 4\vec{a}\cdot \vec{b}=4\vec{b}\cdot \vec{c},\therefore \vec{a}\cdot \vec{b}-\vec{b}\cdot \vec{c}=0\),\(\therefore \vec{b}\cdot (\vec{a}-\vec{c})=0\).
又\(\vec{b}=\overrightarrow{AC}\),\(\vec{a}-\vec{c}=\overrightarrow{DB}\),\(\therefore \overrightarrow{AC}\cdot \overrightarrow{DB}=0\),
\(\therefore \overrightarrow{AC}⊥\overrightarrow{DB}\),\(\therefore AC⊥DB\),同理可证\(AD⊥BC\),\(AB⊥CD\),
\(\therefore\)这个四面体相对的棱丙两垂直. -
【答案】 \(\dfrac{3}{2}\)
【解析】 \(\because △ABC\)是等边三角形,\(\therefore O\)是\(△ABC\)的重心,
延长\(AO\)交\(BC\)于点\(D\),则\(D\)为\(BC\)的中点,\(\therefore \overrightarrow{AD }=\dfrac{1}{2}(\overrightarrow{AB }+\overrightarrow{AC})\),
故\(\overrightarrow{PO}=\overrightarrow{PA}+\overrightarrow{AO}=\overrightarrow{PA}+\dfrac{2}{3} \overrightarrow{AD }=\overrightarrow{AP}+\dfrac{1}{3} (\overrightarrow{AB }+\overrightarrow{AC} )\)\(=\overrightarrow{PA}+\dfrac{1}{3} (\overrightarrow{PB}-\overrightarrow{PA}+\overrightarrow{PC}-\overrightarrow{PA} )\)
\(=\dfrac{1}{3} \overrightarrow{PA}+\dfrac{1}{3} \overrightarrow{PB}+\dfrac{1}{3} \overrightarrow{PC}\),
设\(\overrightarrow{PA}=x\overrightarrow{PM}\),\(\overrightarrow{PB}=y\overrightarrow{PN}\),\(\overrightarrow{PC}=z\overrightarrow{PS}\),
则\(\overrightarrow{PO}=\dfrac{1}{3} x\overrightarrow{PM}+\dfrac{1}{3} y\overrightarrow{PN}+\dfrac{1}{3} z\overrightarrow{PS}\),
\(\because O\),\(M\),\(N\),\(S\)四点共面,\(\therefore \dfrac{1}{3} x+\dfrac{1}{3} y+\dfrac{1}{3} z=1\),即\(x+y+z=3\),
又 \(x=\dfrac{P A}{P M}=\dfrac{2}{P M}\), \(y=\dfrac{P B}{P N}=\dfrac{2}{P N}\), \(z=\dfrac{P C}{P S}=\dfrac{2}{P S}\),
\(\therefore 2\left(\dfrac{1}{P S}+\dfrac{1}{P M}+\dfrac{1}{P N}\right)=3\),
\(\therefore \dfrac{1}{P S}+\dfrac{1}{P M}+\dfrac{1}{P N}=\dfrac{3}{2}\).


