1.3(1) 空间向量及其运算的坐标表示
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学上学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
选择性必修第一册同步提高,难度3颗星!
知识剖析
空间向量的直角坐标系
(1) 空间直角坐标系
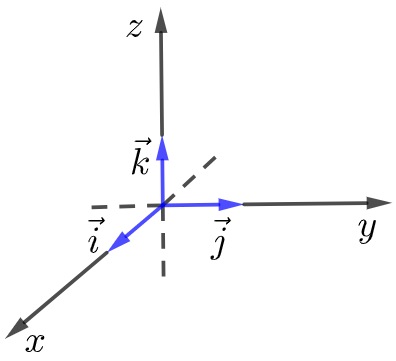
在空间选定一点\(O\)和一个单位正交基底\(\{\vec{\imath}, \vec{\jmath}, \vec{k}\}\),以点\(O\)为原点,分别以\(\vec{\imath}, \vec{\jmath}, \vec{k}\)的方向为正方向、以它们的长为单位长度建立三条数轴:\(x\)轴、\(y\)轴、\(z\)轴,它们都叫做坐标轴,这时我们就建立了一个空间直角坐标系\(Oxyz\),\(O\)叫做原点,\(\vec{\imath}, \vec{\jmath}, \vec{k}\)都叫做坐标向量,通过每两条坐标轴的平面叫做坐标平面,分别称为\(Oxy\)平面,\(Oxz\)平面,\(Oyz\)平面,它们把空间分成八个部分.
在空间直角坐标系中,让右手拇指指向\(x\)轴的正方向,食指指向\(y\)轴的正方向,如果中指指向\(z\)轴的正方向,则称这个坐标系为右手直角坐标系.空间直角坐标系中的坐标
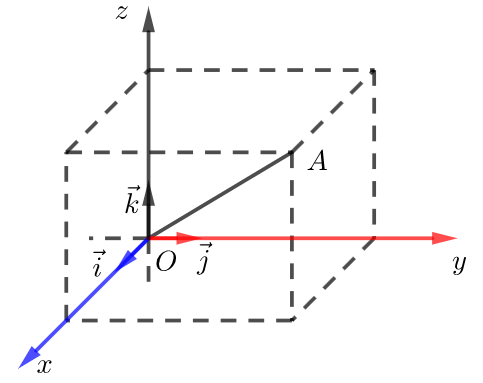
(2) 空间直角坐标系中的坐标
在空间直角坐标系\(O-x y z\)中,对空间任一点\(A\),存在唯一的有序实数组\((x ,y ,z)\),使\(\overrightarrow{O A}=x \vec{\imath}+y \vec{\jmath}+z \vec{k}\) , 有序实数组\((x ,y ,z)\)叫作向量\(A\)在空间直角坐标系 中的坐标,记作\(A(x ,y ,z)\),\(x\)叫横坐标,\(y\)叫纵坐标,\(z\)叫竖坐标.
空间向量的直角坐标运算律
① 若\(\vec{a}=\left(a_{1}, a_{2}, a_{3}\right)\) ,\(\vec{b}=\left(b_{1}, b_{2}, b_{3}\right)\),
则\(\vec{a}+\vec{b}=\left(a_{1}+b_{1}, a_{2}+b_{2}, a_{3}+b_{3}\right)\),\(\vec{a}-\vec{b}=\left(a_{1}-b_{1}, a_{2}-b_{2}, a_{3}-b_{3}\right)\),
\(\lambda \vec{a}=\left(\lambda a_{1}, \lambda a_{2}, \lambda a_{3}\right) \quad(\lambda \in R)\),
\(\vec{a} \cdot \vec{b}=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}\),
\(\vec{a} \| \vec{b} \Rightarrow a_{1}=\lambda b_{1}\), \(a_{2}=\lambda b_{2}\) , \(a_{3}=\lambda b_{3}(\lambda \in R)\),
\(\vec{a} \perp \vec{b} \Rightarrow \vec{a} \cdot \vec{b}=0 \Rightarrow a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}=0\),
② 若\(A(x_1 ,y_1 ,z_1 )\), \(B(x_2 ,y_2 ,z_2 )\),则\(\overrightarrow{A B}=\left(x_{2}-x_{1}, y_{2}-y_{1}, z_{2}-z_{1}\right)\).
③ 模长公式
若\(\vec{a}=\left(a_{1}, a_{2}, a_{3}\right)\),则\(|\vec{a}|=\sqrt{\vec{a} \cdot \vec{a}}=\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}\),
④ 夹角公式
\(\cos \langle\vec{a}, \vec{b}\rangle=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot|\vec{b}|}=\dfrac{a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}} \sqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}\)
\(∆ABC\)中 ,\(\overrightarrow{A B} \cdot \overrightarrow{A C}>0 \Rightarrow\)\(A\)为锐角, \(\overrightarrow{A B} \cdot \overrightarrow{A C}<0 \Rightarrow\)\(A\)为钝角.
⑤ 两点间的距离公式
若\(A(x_1 ,y_1 ,z_1)\),\(B(x_2 ,y_2 ,z_2)\)
则\(|\overrightarrow{A B}|=\sqrt{\overrightarrow{A B^{2}}}=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\)
或\(d_{A B}=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\).
经典例题
【题型一】空间向量坐标运算
【典题1】 已知:\(\vec{a}=(x,4,1)\),\(\vec{b}=(-2,y,-1)\),\(\vec{c}=(3,-2,z)\),\(\vec{a}//\vec{b}\),\(\vec{b}⊥\vec{c}\),求:
(1)\(\vec{a}\),\(\vec{b}\),\(\vec{c}\); \(\qquad \qquad\) (2)\(\vec{a}+\vec{c}\)与\(\vec{b}+\vec{c}\)所成角的余弦值.
【解析】 (1)\(\because \vec{a}//\vec{b}\), \(\therefore \dfrac{x}{-2}=\dfrac{4}{y}=\dfrac{1}{-1}\),解得\(x=2\),\(y=-4\),
故\(\vec{a}=(2,4,1)\),\(\vec{b}=(-2,-4,-1)\),
又因为\(\vec{b}⊥\vec{c}\),所以\(\vec{b}\cdot \vec{c}=0\),即\(-6+8-z=0\),解得\(z=2\),
故 \(\vec{c}=(3,-2,2)\);
(2)由(1)可得\(\vec{a}+\vec{c}=(5,2,3)\),\(\vec{b}+\vec{c}=(1,-6,1)\),
设向量\(\vec{a}+\vec{c}与\vec{b}+\vec{c}\)所成的角为\(\theta\),
则 \(\cos \theta=\dfrac{5-12+3}{\sqrt{38} \cdot \sqrt{38}}=-\dfrac{2}{19}\).
【典题2】 已知空间四点\(A(2,-1,1)\)、\(B(1,2 ,3)\)、\(C(0 ,2 ,1)\)、\(D(1 ,0 ,λ)\)在同一平面内,则实数\(λ=\)\(\underline{\quad \quad}\) .
【解析】 \(∵\)空间四点\(A(2,-1,1)\)、\(B(1,2 ,3)\)、\(C(0 ,2 ,1)\)、\(D(1 ,0 ,λ)\)在同一平面内,
\(\therefore \overrightarrow{A D}=m \overrightarrow{A B}+n \overrightarrow{A C}\),
即\((-1,1, \lambda-1)=m(-1,3,2)+n(-2,3,0)=(-m-2 n, 3 m+3 n, 2 m)\)
\(\therefore\left\{\begin{array}{l}
-m-2 n=-1 \\
3 m+3 n=1 \\
2 m=\lambda-1
\end{array}\right.\),解得\(m=-\dfrac{1}{3}\),\(n=\dfrac{2}{3}\),\(\lambda=\dfrac{1}{3}\).
\(∴\)实数\(\lambda=\dfrac{1}{3}\).
【点拨】 若\(A\)、\(B\)、\(C\)、\(P\)四点共面\(\Rightarrow \overrightarrow{A P}=x \overrightarrow{A B}+y \overrightarrow{A C}\).
巩固练习
1(★) 空间点\(A(x,y,z)\),\(O(0,0,0)\),\(B(\sqrt{2},\sqrt{3},2)\),若\(|AO|=1\),则\(|AB\)|的最小值为 \(\underline{\quad \quad}\) .
2(★) 已知向量\(\vec{a}=(2,-1,3)\),\(\vec{b}=(-4,2,t)\)的夹角为钝角,则实数\(t\)的取值范围为\(\underline{\quad \quad}\) .
3(★) 若向量\(\vec{a}=(7,λ,8)\),\(\vec{b}=(1,-1,2)\),\(\vec{c}=(2,3,1)\),且\(\vec{a}\),\(\vec{b}\),\(\vec{c}\)共面,则\(λ=\)\(\underline{\quad \quad}\).
4(★★) 已知\(\overrightarrow{A B}=(2,-1,3)\),\(\overrightarrow{A C}=(-1,4,-2)\),\(\overrightarrow{A D}=(5,-6,λ)\),若\(A\),\(B\),\(C\),\(D\)四点共面,则实数\(λ\)为\(\underline{\quad \quad}\) .
参考答案
-
【答案】 \(2\)
【解析】 \(\because\)空间点\(A(x,y,z)\),\(O(0,0,0)\),\(B(\sqrt{2},\sqrt{3},2)\),若\(|AO|=1\),,
\(\therefore A\)是以\(O\)为球心,\(1\)为半径的球上的点,
\(\because B(\sqrt{2},\sqrt{3},2)\), \(\therefore|O B|=\sqrt{(\sqrt{2})^2+(\sqrt{3})^2+2^2}=3\).
\(\therefore |AB|\)的最小值为:\(|OB|-||OA|=3-1=2\). -
【答案】 \((-\infty,-6) \cup\left(-6, \dfrac{10}{3}\right)\)
【解析】 \(\because\)向量\(\vec{a}=(2,-1,3)\),\(\vec{b}=(-4,2,t)\)的夹角为钝角,
\(\therefore\left\{\begin{array}{l} \vec{a} \cdot \vec{b}=-8-2+3 t<0 \\ t \neq-6 \end{array}\right.\),解得\(t<\dfrac{10}{3}\),且\(t≠-6\),
\(\therefore\)实数\(t\)的取值范围为\((-\infty,-6) \cup\left(-6, \dfrac{10}{3}\right)\). -
【答案】 \(3\)
【解析】 向量 \(\vec{a}=(7,λ,8)\),\(\vec{b}=(1,-1,2)\),\(\vec{c}=(2,3,1)\),
且\(\vec{a}\),\(\vec{b}\),\(\vec{c}\)共面,
所以存在两个实数\(x\)、\(y\)使得\(\vec{a}=x\vec{b}+y\vec{c}\);
即 \(\left\{\begin{array}{l} 7=x+2 y \\ \lambda=-x+3 y \\ 8=2 x+y \end{array}\right.\),解得 \(\left\{\begin{array}{l} x=3 \\ y=2 \\ \lambda=3 \end{array}\right.\);所以\(λ=3\). -
【答案】 \(8\)
【解析】 \(\because A\),\(B\),\(C\),\(D\)四点共面,\(\therefore\)存在实数\(m\),\(n\),使得\(\overrightarrow{A D}=m\overrightarrow{A B}+n\overrightarrow{A C}\),
\(\therefore\left\{\begin{array}{l} 2 m-n=5 \\ -m+4 n=-6 \\ 3 m-2 n=\lambda \end{array}\right.\),解得\(\left\{\begin{array}{l} m=2 \\ n=-1 \\ \lambda=8 \end{array}\right.\).
【题型二】建立空间坐标系处理几何问题
【典题1】 \(△ABC\)的三个顶点分别是\(A(1 ,-1 ,2)\),\(B(5 ,-6 ,2)\),\(C(1 ,3 ,-1)\),则\(AC\)边上的高\(BD\)长\(\underline{\quad \quad}\).
【解析】
方法一 要求高\(BD\),则只需求点\(D\)坐标,可采取待定系数法.
设点\(D(x、y、z)\),
则\(\overrightarrow{B D}=(x-5, y+6, z-2)\),\(\overrightarrow{A D}=(x-1, y+1, z-2)\),\(\overrightarrow{A C}=(0,4,-3)\),
由垂足\(D\)满足的条件
\(\left\{\begin{array} { l }
{ \overrightarrow{B D}\cdot \overrightarrow{AC}= 0 } \\
{ \overrightarrow{AD} / / \overrightarrow{AC}}
\end{array} \Rightarrow \left\{\begin{array} { l }
{ 4 ( y + 6 ) - 3 ( z - 2 ) = 0 } \\
{ ( x - 1 , y + 1 , z - 2 ) = \lambda ( 0 , 4 , - 3 ) }
\end{array} \Rightarrow \left\{\begin{array}{l}
x=1 \\
y=-\dfrac{21}{5} \\
z=\dfrac{22}{5}
\end{array}\right.\right.\right.\);
\(\therefore \overrightarrow{B D}=\left(-4, \dfrac{9}{5}, \dfrac{12}{5}\right)\),
\(\therefore|\overrightarrow{B D}|=\sqrt{4^{2}+\left(\dfrac{9}{5}\right)^{2}+\left(\dfrac{12}{5}\right)^{2}}=5\).
方法二 等积法
(思考:因为三个点\({\color{Red}{ A}}\)、\({\color{Red}{B }}\)、\({\color{Red}{C }}\)确定了,则可求出\({\color{Red}{ ∆ABC}}\)的面积\({\color{Red}{ S_{ABC}}}\),继而可求高\({\color{Red}{B D=\dfrac{2 S_{A B C}}{A C} }}\))
\(∵A(1 ,-1 ,2)\),\(B(5 ,-6 ,2)\),\(C(1 ,3 ,-1)\),
\(\therefore \overrightarrow{A C}=(0,4,-3)\),\(\overrightarrow{A B}=(4,-5,0)\),
\(\therefore \cos A=\dfrac{\overrightarrow{A C} \cdot \overrightarrow{A B}}{|\overrightarrow{A C}| \cdot|\overrightarrow{A B}|}=\dfrac{-20}{5 \times \sqrt{41}}=-\dfrac{4}{\sqrt{41}} \Rightarrow \sin A=\dfrac{5}{\sqrt{41}}\),
\(\therefore S_{A B C}=\dfrac{1}{2}|\overrightarrow{A C}| \cdot|\overrightarrow{A B}| \sin A=\dfrac{25}{2},\) ,
\(\because S_{A B C}=\dfrac{1}{2} B D \times A C\) ,
\(\therefore B D=\dfrac{2 S_{A B C}}{A C}=\dfrac{25}{5}=5 .\).
【点拨】 我们利用空间向量的知识也是可以求出几何中常见的量:线段长度(两点距离公式)、角度(数量积)、面积等.
【典题2】 如图,\(BC=4\),原点\(O\)是\(BC\)的中点,点\(A\left(\dfrac{\sqrt{3}}{2}, \dfrac{1}{2}, 0\right)\),点\(D\)在平面\(yOz\)上,且\(∠BDC=90^{\circ}\),\(∠DCB=30^{\circ}\),则\(AD\)的长度为\(\underline{\quad \quad}\).

【解析】 \(∵\)点\(D\)在平面\(yoz\)上,\(∴\)点\(D\)的横坐标为\(0\),
过点\(D\)作\(DH⊥BC\),

依题意易得\(D H=4 \sin 30^{\circ} \sin 60^{\circ}=\sqrt{3}\),\(O H=O B-B H=2-4 \sin 30^{\circ} \cos 60^{\circ}=1\),
即点\(D\)的竖坐标为\(z=\sqrt{3}\),纵坐标为\(y=-1\),
\(\therefore D(0,-1, \sqrt{3})\),
\(\therefore|A D|=\sqrt{\left(\dfrac{\sqrt{3}}{2}\right)^{2}+\left(\dfrac{1}{2}+1\right)^{2}+(\sqrt{3})^{2}}=\sqrt{6}\).
【点拨】
① 在空间坐标系中确定点的坐标是个硬骨头,基本方法是:
(1) 根据题意求出各线段长度,比如\(CD\)、\(BD\);
(2) 确定空间点坐标的意义,比如点\(D\)的竖坐标与点\(D\)到平面\(xOy\)的距离有关;
(3) 把空间问题平面化;
(4) 留意\(D\)坐标的正负.
② 两点间的距离公式:若\(A(x_1 ,y_1 ,z_1)\) ,\(B(x_2 ,y_2 ,z_2)\),
则\(|\overrightarrow{A B}|=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\).
【典题3】 如图,直角三角形\(OAC\)所在平面与平面\(α\)交于\(OC\),平面\(OAC⊥\)平面\(α\),\(∠OAC\)为直角,\(OC=4\),\(B\)为\(OC\)的中点,且\(\angle A B C=\dfrac{2 \pi}{3}\),平面\(α\)内一动点\(P\)满足\(\angle P A B=\dfrac{\pi}{3}\),则\(\overrightarrow{O P} \cdot \overrightarrow{C P}\)的取值范围是\(\underline{\quad \quad}\).

【解析】
(题中垂直关系较多,较容易建系描出各点坐标,进而数量积\({\color{Red}{ \overrightarrow{O P} \cdot \overrightarrow{C P}}}\)易于用某个变量表示,再用函数的方法求其范围)
\(∵\)平面\(OAC⊥\)平面\(α\),
\(∴\)作\(AO'⊥OC\),则\(AO'⊥\)平面\(α\),
过\(O'\)在平面\(α\)内作\(OC\)的垂线\(O'X\),如图建立空间直角坐标系\(O'-XYZ\),

\(∵∠OAC\)为直角,\(OC=4\),\(B\)为\(OC\)的中点,且\(\angle A B C=\dfrac{2 \pi}{3}\), (利用平几知识)
\(∴BC=AB=OB=2\),\(\angle A B O=\dfrac{\pi}{3}\),
\(O^{\prime} A=\sqrt{3}\),\(O'B=1\),\(OO'=1\),\(O'C=3\),
则\(O(0 ,-1 ,0)\),\(A(0,0, \sqrt{3})\),\(B(0 ,1 ,0)\),\(C(0 ,3 ,0)\),
设\(P(x ,y ,0)\),
(点\(P\)是动点,在坐标系中引入变量\(x\),\(y\),再由限制条件\(\angle P A B=\dfrac{\pi}{3}\)得到\(x\),\(y\)的关系)
则\(\overrightarrow{A P}=(x, y,-\sqrt{3})\),\(\overrightarrow{A B}=(0,1,-\sqrt{3})\),
\(\therefore \overrightarrow{A P} \cdot \overrightarrow{A B}=y+3\),
\(\because \angle P A B=\dfrac{\pi}{3}\)
\(\therefore \overrightarrow{A P} \cdot \overrightarrow{A B}=|\overrightarrow{A P}||\overrightarrow{A B}| \cos \angle P A B=2 \sqrt{x^{2}+y^{2}+3} \cdot \dfrac{1}{2}=\sqrt{x^{2}+y^{2}+3}\),
\(\therefore y+3=\sqrt{x^{2}+y^{2}+3} \Rightarrow x^{2}=6 y+6\),(点\(P\)的轨迹是抛物线)
\(\therefore \overrightarrow{O P} \cdot \overrightarrow{C P}=x^{2}+(y+1)(y-3)\)\(=6 y+6+y^{2}-2 y-3=y^{2}+4 y+3=(y+2)^{2}-1\),
又\(∵x^2=6y+6≥0\),
\(∴y≥-1\),
(点\(P\)是有固定轨迹的,即\(y\)是有范围的,讨论函数性质也要优先讨论定义域)
\(∴\)当\(y=-1\)时,\(\overrightarrow{O P} \cdot \overrightarrow{C P}\)的最小值为\(0\),
\(\therefore \overrightarrow{O P} \cdot \overrightarrow{C P} \geq 0\).
故答案为\([0 ,+∞)\).
【点拨】
① 由平面OAC⊥平面α可想到建立空间直角坐标系的方法,根据\(∆OAC\)已知条件可求其他角、边的大小,从而得到各点的坐标;
② 而\(\overrightarrow{O P} \cdot \overrightarrow{C P}\)由点\(P\)确定,能否求出其轨迹呢?而利用建坐标系的方法,较容易得到其轨迹(学圆锥曲线后也可知轨迹是抛物线);
③ 从数量积坐标运算的角度得\(\overrightarrow{A P} \cdot \overrightarrow{A B}=y+3\),从数量积的定义\(\overrightarrow{A P} \cdot \overrightarrow{A B}=\sqrt{x^{2}+y^{2}+3}\),从而得到点\(P\)的轨迹\(x^2=6y+6\);
④ 由坐标运算易求\(\overrightarrow{O P} \cdot \overrightarrow{C P}\)最小值化为\((y+2)^2-1\)的最小值,这里有函数思想,注意函数的定义域;
⑤ 本题若想用非坐标的方法解答:
\(\overrightarrow{O P} \cdot \overrightarrow{C P}=(\overrightarrow{O B}+\overrightarrow{B P})(\overrightarrow{C B}+\overrightarrow{B P})\)\(\overrightarrow{O B} \cdot \overrightarrow{C B}+\overrightarrow{B P}(\overrightarrow{O B}+\overrightarrow{C B})+\overrightarrow{B P}^{2}=|B P|^{2}-4\),
而得不到点\(P\)的轨迹,较难求出\(|BP|^2\)的范围!
巩固练习
1(★) 如图三棱柱\(ABC-A_1 B_1 C_1\)中,侧面\(BB_1 C_1 C\)是边长为\(2\)菱形,\(∠CBB_1=60^{\circ}\),\(BC_1\)交\(B_1 C\)于点\(O\),\(AO⊥\)侧面\(BB_1 C_1 C\),且\(△AB_1 C\)为等腰直角三角形,如图建立空间直角坐标系\(O-xyz\),则点\(A_1\)的坐标为\(\underline{\quad \quad}\) .

2 (★★) 已知点\(A(1,-2,11)\)、\(B(4,2,3)\),\(C(6,-1,4)\),则\(△ABC\)中角\(C\)的大小是\(\underline{\quad \quad}\).
3(★★) 已知空间三点\(A(0 ,2 ,3)\),\(B(2 ,5 ,2)\),\(C(-2 ,3 ,6)\),则以\(AB\),\(AC\)为邻边的平行四边形的面积为\(\underline{\quad \quad}\).
4 (★★★) 已知长方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(AB=4\),\(BC=3\),\(AA_1=2\),空间中存在一动点\(P\)满足\(\left|\overrightarrow{B_{1} P}\right|=1\),记\(I_{1}=\overrightarrow{A B} \cdot \overrightarrow{A P}\),\(I_{2}=\overrightarrow{A D} \cdot \overrightarrow{A P}\),\(I_{3}=\overrightarrow{A C_{1}} \cdot \overrightarrow{A P}\),则( )
A.存在点\(P\),使得\(I_1=I_2\)
B.存在点\(P\),使得\(I_1=I_3\)
C.对任意的点\(P\),有\(I_1>I_2\)
D.对任意的点\(P\),有\(I_2>I_3\)
5(★★★) 如图,已知点\(P\)在正方体\(ABCD-A'B'C'D'\)的对角线\(BD'\)上,\(∠PDC=60^{\circ}\).设\(\overrightarrow{D^{\prime} P}=\lambda \overrightarrow{D^{\prime} B}\),则\(λ\)的值为\(\underline{\quad \quad}\).

6(★★★) 三棱锥\(O-ABC\)中,\(OA\),\(OB\),\(OC\)两两垂直且相等,点\(P\),\(Q\)分别是线段\(BC\)和\(OA\)上移动,且满足\(B P \leq \dfrac{1}{2} B C\),\(A Q \leq \dfrac{1}{2} A O\),则\(PQ\)和\(OB\)所成角余弦值的取值范围是\(\underline{\quad \quad}\).
参考答案
- 【答案】 \((-\sqrt{3}, 1,1)\)
【解析】 三棱柱\(ABC-A_1 B_1 C_1\)中,侧面\(BB_1 C_1 C\)是边长为\(2\)菱形,\(∠CBB_1=60^{\circ}\),\(BC_1\)交\(B_1 C\)于点\(O\),\(AO⊥\)侧面\(BB_1 C_1 C\),且\(△AB_1 C\)为等腰直角三角形,
如图建立空间直角坐标系\(O-xyz\),
过\(A_1\)作\(A_1 E⊥\)平面\(BCC_1 B_1\),垂足是\(E\),连结\(B_1 E\),\(C_1 E\),
则\(B_1 E∥OC_1\),\(C_1 E∥OB_1\),\(A_1 E∥AO\),
\(∴\)点\(A_1\)的坐标为\((-\sqrt{3}, 1,1)\).
故选:\(B\).

- 【答案】 \(90°\)
【解析】 \(∵A(1,-2,11)\)、\(B(4,2,3)\),\(C(6,-1,4)\),
\(\therefore|\overrightarrow{A C}|=\sqrt{(1-6)^{2}+(-2+1)^{2}+(11-4)^{2}}=\sqrt{75}\)
\(|\overrightarrow{B C}|=\sqrt{(4-6)^{2}+(2+1)^{2}+(3-4)^{2}}=\sqrt{14}\)
又\(\because \overrightarrow{C A}=(-5,-1,7), \quad \overrightarrow{C B}=(-2,3,-1)\)
\(\therefore \overrightarrow{C A} \cdot \overrightarrow{C B}=(-5) \times(-2)+(-1) \times 3+7 \times(-1)=0\)
可得\(\cos \angle A C B=\dfrac{\overrightarrow{C A} \cdot \overrightarrow{C B}}{|\overrightarrow{C A \mid}| \times|\overrightarrow{C B}|}=0\)
\(∵∠ACB∈(0^{\circ},180^{\circ})\) \(∴∠ACB=90^{\circ}\)
故答案为\(90^{\circ}\) - 【答案】 \(6 \sqrt{5}\)
【解析】 \(\overrightarrow{A B}=(2,3,-1)\),\(\overrightarrow{A C}=(-2,1,3)\)
\(\therefore \overrightarrow{A B} \cdot \overrightarrow{A C}=-4+3-3=-4\),
\(|\overrightarrow{A B}|=\sqrt{2^{2}+3^{2}+(-1)^{2}}=\sqrt{14}\),\(|\overrightarrow{A C}|=\sqrt{(-2)^{2}+1^{2}+3^{2}}=\sqrt{14}\).
\(\therefore \cos \angle B A C=\dfrac{\overrightarrow{A B} \cdot \overrightarrow{A C}}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}=\dfrac{-4}{\sqrt{14} \times \sqrt{14}}=-\dfrac{2}{7}\).
\(\therefore \sin \angle B A C=\sqrt{1-\cos ^{2} \angle A B C}=\dfrac{3 \sqrt{5}}{7}\).
\(∴\)以\(AB,AC\)为邻边的平行四边形的面积
\(S=|\overrightarrow{A B}| \cdot|\overrightarrow{A C}| \cdot \sin \angle B A C=\sqrt{14} \times \sqrt{14} \times \dfrac{3 \sqrt{5}}{7}=6 \sqrt{5}\).
故答案为:\(6√5\). - 【答案】 \(C\)
【解析】 如图所示

建立如图所示的空间直角坐标系,以\(B_1 A_1\)为\(x\)轴,\(B_1 C_1\)为\(y\)轴,\(B_1 B\)为\(z\)轴,\(B_1\)为坐标原点,由题意则\(B(0,0,2)\),\(A(4,0,2)\),\(D(4,3,2)\),\(C_1 (0,3,0)\),设\(P(x,y,z)\),
所以\(\overrightarrow{A B}=(-4,0,0)\),\(\overrightarrow{A P}=(x-4, y, z-2)\),\(\overrightarrow{A D}=(0,3,0)\),
\(\overrightarrow{A C_{1}}=(-4,3,-2)\),\(\overrightarrow{B_{1} P}=(x, y, z)\),
因为满足\(\left|\overrightarrow{B_{1} P}\right|=1\),
所以\(x^{2}+y^{2}+z^{2}=1\),\(x∈[-1,1]\),\(y∈[-1,1]\),\(z∈[-1,1]\),
\(\therefore I_{1}=\overrightarrow{A B} \cdot \overrightarrow{A P}=-4(x-4)\),
\(\therefore I_{2}=\overrightarrow{A D} \cdot \overrightarrow{A P}=3 y\)
\(\therefore I_{3}=\overrightarrow{A C}_{1} \cdot \overrightarrow{A P}=-4(x-4)+3 y-2(z-2)\),
\(I_{1}-I_{2}=-4(x-4)-3 y=16-4 x-3 y>0\)恒成立,故\(C\)正确,\(A\)不正确;
\(I_{1}-I_{3}=-3 y+2(z-2)=-4-3 y+2 z<0\)恒成立,所以\(B\)不正确,
\(I_2-I_3=4(x-4)+2(z-2)=-12+4x+2z<0\)恒成立,所以\(D\)不正确;
故选:\(C\). - 【答案】 \(\sqrt{2}-1\)
【解析】 以\(D\)为原点,\(DA\)为\(x\)轴,\(DC\)为\(y\)轴,\(DD'\)为\(z\)轴,建立空间直角坐标系,
设正方体\(ABCD-A'B'C'D'\)的棱长为\(1\),
点\(P\)在正方体\(ABCD-A'B'C'D'\)的对角线\(BD'\)上,且\(∠PDA=60^{\circ}\),
\(\because \overrightarrow{D^{\prime}} P=\lambda \overrightarrow{D^{\prime}} B, \quad(0<\lambda<1)\)
则\(A(1,0,0)\),\(C(0,1,0)\),\(D'(0,0,1)\),\(B(1,1,0)\),\(P(\lambda, \lambda, 1-\lambda)\),
\(\therefore \overrightarrow{D P}=(\lambda, \lambda, 1-\lambda), \quad \overrightarrow{D C}=(0,1,0)\),
\(\therefore \cos <\overrightarrow{D C}, \overrightarrow{D P}>=\dfrac{\overrightarrow{D C} \cdot \overrightarrow{D P}}{|\overrightarrow{D C}| \times|\overrightarrow{D P}|}=\dfrac{\lambda}{1 \times \sqrt{\lambda^{2}+\lambda^{2}+(1-\lambda)^{2}}}=\cos 60^{\circ}=\dfrac{1}{2}\),
由\(0<λ<1\),解得\(\lambda=\sqrt{2}-1\).
故选:\(C\).

- 【答案】 \(\left[\dfrac{\sqrt{6}}{6}, \dfrac{2 \sqrt{5}}{5}\right]\)
【解析】 如图所示,不妨取\(OA=2\).则\(B(0,2,0)\),\(C(0,0,2)\).
设\(P(0,y,z)\),\(\overrightarrow{B P}=\lambda \overrightarrow{B C}\)\(\left(0 \leq \lambda \leq \dfrac{1}{2}\right)\).
则\((0, y-2, z)=\lambda(0,-2,2)=(0,-2 \lambda, 2 \lambda)\),
\(\therefore\left\{\begin{array}{l} y-2=-2 \lambda \\ z=2 \lambda \end{array}\right.\),解得\(y=2-2 \lambda\),\(z=2 \lambda\).
\(\therefore P(0,2-2 \lambda, 2 \lambda)\).
设\(Q(m,0,0)\),\(\left(\dfrac{1}{2} \leq m \leq 1\right)\),则\(\overrightarrow{P Q}=(m, 2 \lambda-2,-2 \lambda)\),
又\(\overrightarrow{O B}=(0,2,0)\),
\(\therefore \cos <\overrightarrow{P Q}, \overrightarrow{O B}>=\dfrac{\overrightarrow{P Q} \cdot \overrightarrow{O B}}{\overrightarrow{P Q|| \overrightarrow{O B} \mid}}=\dfrac{1-\lambda}{\sqrt{m^{2}+(1-\lambda)^{2}+\lambda^{2}}}\).
①当点\(P\)取\(B(0,1,0)\)时,取\(Q\left(\dfrac{1}{2}, 0,0\right)\)时,\(m=\dfrac{1}{2}\),\(λ=0\),
则\(\cos <\overrightarrow{P Q}, \overrightarrow{O B}>=\dfrac{1}{\sqrt{\left(\dfrac{1}{2}\right)^{2}+1}}=\dfrac{2 \sqrt{5}}{5}\).
取\(Q(1,0,0)\)时,\(m=1\),\(λ=0\),\(\cos <\overrightarrow{P Q}, \overrightarrow{O B}>=\dfrac{\sqrt{2}}{2}\).
②当点\(P\)取\(B\left(0, \dfrac{1}{2}, \dfrac{1}{2}\right)\)时,取\(Q\left(\dfrac{1}{2}, 0,0\right)\)时,\(m=\dfrac{1}{2}\),\(\lambda=\dfrac{1}{2}\),
则\(\cos <\overrightarrow{P Q}, \overrightarrow{O B}>=\dfrac{\dfrac{1}{2}}{\sqrt{\left(\dfrac{1}{2}\right)^{2}+\left(\dfrac{1}{2}\right)^{2} \times 2}}=\dfrac{\sqrt{3}}{3}\).
取\(Q(1,0,0)\)时,\(m=1\),\(\lambda=\dfrac{1}{2}\),
\(\cos <\overrightarrow{P Q}, \overrightarrow{O B}>=\dfrac{\dfrac{1}{2}}{\sqrt{1^{2}+\left(\dfrac{1}{2}\right)^{2} \times 2}}=\dfrac{\sqrt{6}}{6}\).
综上可得:\(PQ\)和\(OB\)所成角余弦值的取值范围是\(\left[\dfrac{\sqrt{6}}{6}, \dfrac{2 \sqrt{5}}{5}\right]\).


